Dadas dos strings ‘X’ e ‘Y’, encuentre la longitud de la substring común más larga.
Ejemplos:
Entrada: X = «GeeksforGeeks», y = «GeeksQuiz»
Salida : 5
Explicación:
La substring común más larga es «Geeks» y tiene una longitud de 5.Entrada: X = “abcdxyz”, y = “xyzabcd”
Salida: 4
Explicación:
La substring común más larga es “abcd” y tiene una longitud de 4.Entrada: X = “zxabcdezy”, y = “yzabcdezx”
Salida: 6
Explicación:
La substring común más larga es “abcdez” y tiene una longitud de 6.

Enfoque:
Sean m y n las longitudes de la primera y segunda string respectivamente.
Una solución simple es considerar una por una todas las substrings de la primera string y para cada substring verificar si es una substring en la segunda string. Mantenga un registro de la substring de longitud máxima. Habrá O(m^2) substrings y podemos encontrar si una string es una substring en otra string en tiempo O(n) (Ver esto ). Entonces, la complejidad temporal general de este método sería O(n * m 2 )
La programación dinámica se puede utilizar para encontrar la substring común más larga en tiempo O(m*n). La idea es encontrar la longitud del sufijo común más largo para todas las substrings de ambas strings y almacenar estas longitudes en una tabla.
El sufijo común más largo tiene la siguiente propiedad de subestructura óptima.
Si los últimos caracteres coinciden, entonces reducimos ambas longitudes en 1
LCSuff(X, Y, m, n) = LCSuff(X, Y, m-1, n-1) + 1 si X[m-1] = Y[n -1]
Si los últimos caracteres no coinciden, el resultado es 0, es decir,
LCSuff(X, Y, m, n) = 0 if (X[m-1] != Y[n-1])
Ahora consideramos los sufijos de diferentes substrings que terminan en diferentes índices.
El sufijo común más largo de longitud máxima es la substring común más larga.
LCSubStr(X, Y, m, n) = Max(LCSuff(X, Y, i, j)) donde 1 <= i <= m y 1 <= j <= n
A continuación se muestra la implementación iterativa de la solución anterior.
C++
/* Dynamic Programming solution to
find length of the
longest common substring */
#include <iostream>
#include <string.h>
using namespace std;
/* Returns length of longest
common substring of X[0..m-1]
and Y[0..n-1] */
int LCSubStr(char* X, char* Y, int m, int n)
{
// Create a table to store
// lengths of longest
// common suffixes of substrings.
// Note that LCSuff[i][j] contains
// length of longest common suffix
// of X[0..i-1] and Y[0..j-1].
int LCSuff[m + 1][n + 1];
int result = 0; // To store length of the
// longest common substring
/* Following steps build LCSuff[m+1][n+1] in
bottom up fashion. */
for (int i = 0; i <= m; i++)
{
for (int j = 0; j <= n; j++)
{
// The first row and first column
// entries have no logical meaning,
// they are used only for simplicity
// of program
if (i == 0 || j == 0)
LCSuff[i][j] = 0;
else if (X[i - 1] == Y[j - 1]) {
LCSuff[i][j] = LCSuff[i - 1][j - 1] + 1;
result = max(result, LCSuff[i][j]);
}
else
LCSuff[i][j] = 0;
}
}
return result;
}
// Driver code
int main()
{
char X[] = "OldSite:GeeksforGeeks.org";
char Y[] = "NewSite:GeeksQuiz.com";
int m = strlen(X);
int n = strlen(Y);
cout << "Length of Longest Common Substring is "
<< LCSubStr(X, Y, m, n);
return 0;
}
Java
// Java implementation of
// finding length of longest
// Common substring using
// Dynamic Programming
class GFG {
/*
Returns length of longest common substring
of X[0..m-1] and Y[0..n-1]
*/
static int LCSubStr(char X[], char Y[],
int m, int n)
{
// Create a table to store
// lengths of longest common
// suffixes of substrings.
// Note that LCSuff[i][j]
// contains length of longest
// common suffix of
// X[0..i-1] and Y[0..j-1].
// The first row and first
// column entries have no
// logical meaning, they are
// used only for simplicity of program
int LCStuff[][] = new int[m + 1][n + 1];
// To store length of the longest
// common substring
int result = 0;
// Following steps build
// LCSuff[m+1][n+1] in bottom up fashion
for (int i = 0; i <= m; i++)
{
for (int j = 0; j <= n; j++)
{
if (i == 0 || j == 0)
LCStuff[i][j] = 0;
else if (X[i - 1] == Y[j - 1])
{
LCStuff[i][j]
= LCStuff[i - 1][j - 1] + 1;
result = Integer.max(result,
LCStuff[i][j]);
}
else
LCStuff[i][j] = 0;
}
}
return result;
}
// Driver Code
public static void main(String[] args)
{
String X = "OldSite:GeeksforGeeks.org";
String Y = "NewSite:GeeksQuiz.com";
int m = X.length();
int n = Y.length();
System.out.println(LCSubStr(X.toCharArray(),
Y.toCharArray(), m,
n));
}
}
// This code is contributed by Sumit Ghosh
Python3
# Python3 implementation of Finding
# Length of Longest Common Substring
# Returns length of longest common
# substring of X[0..m-1] and Y[0..n-1]
def LCSubStr(X, Y, m, n):
# Create a table to store lengths of
# longest common suffixes of substrings.
# Note that LCSuff[i][j] contains the
# length of longest common suffix of
# X[0...i-1] and Y[0...j-1]. The first
# row and first column entries have no
# logical meaning, they are used only
# for simplicity of the program.
# LCSuff is the table with zero
# value initially in each cell
LCSuff = [[0 for k in range(n+1)] for l in range(m+1)]
# To store the length of
# longest common substring
result = 0
# Following steps to build
# LCSuff[m+1][n+1] in bottom up fashion
for i in range(m + 1):
for j in range(n + 1):
if (i == 0 or j == 0):
LCSuff[i][j] = 0
elif (X[i-1] == Y[j-1]):
LCSuff[i][j] = LCSuff[i-1][j-1] + 1
result = max(result, LCSuff[i][j])
else:
LCSuff[i][j] = 0
return result
# Driver Code
X = 'OldSite:GeeksforGeeks.org'
Y = 'NewSite:GeeksQuiz.com'
m = len(X)
n = len(Y)
print('Length of Longest Common Substring is',
LCSubStr(X, Y, m, n))
# This code is contributed by Soumen Ghosh
C#
// C# implementation of finding length of longest
// Common substring using Dynamic Programming
using System;
class GFG {
// Returns length of longest common
// substring of X[0..m-1] and Y[0..n-1]
static int LCSubStr(string X, string Y, int m, int n)
{
// Create a table to store lengths of
// longest common suffixes of substrings.
// Note that LCSuff[i][j] contains length
// of longest common suffix of X[0..i-1]
// and Y[0..j-1]. The first row and first
// column entries have no logical meaning,
// they are used only for simplicity of
// program
int[, ] LCStuff = new int[m + 1, n + 1];
// To store length of the longest common
// substring
int result = 0;
// Following steps build LCSuff[m+1][n+1]
// in bottom up fashion
for (int i = 0; i <= m; i++)
{
for (int j = 0; j <= n; j++)
{
if (i == 0 || j == 0)
LCStuff[i, j] = 0;
else if (X[i - 1] == Y[j - 1])
{
LCStuff[i, j]
= LCStuff[i - 1, j - 1] + 1;
result
= Math.Max(result, LCStuff[i, j]);
}
else
LCStuff[i, j] = 0;
}
}
return result;
}
// Driver Code
public static void Main()
{
String X = "OldSite:GeeksforGeeks.org";
String Y = "NewSite:GeeksQuiz.com";
int m = X.Length;
int n = Y.Length;
Console.Write("Length of Longest Common"
+ " Substring is "
+ LCSubStr(X, Y, m, n));
}
}
// This code is contributed by Sam007.
PHP
<?php
// Dynamic Programming solution to find
// length of the longest common substring
// Returns length of longest common
// substring of X[0..m-1] and Y[0..n-1]
function LCSubStr($X, $Y, $m, $n)
{
// Create a table to store lengths of
// longest common suffixes of substrings.
// Notethat LCSuff[i][j] contains length
// of longest common suffix of X[0..i-1]
// and Y[0..j-1]. The first row and
// first column entries have no logical
// meaning, they are used only for
// simplicity of program
$LCSuff = array_fill(0, $m + 1,
array_fill(0, $n + 1, NULL));
$result = 0; // To store length of the
// longest common substring
// Following steps build LCSuff[m+1][n+1]
// in bottom up fashion.
for ($i = 0; $i <= $m; $i++)
{
for ($j = 0; $j <= $n; $j++)
{
if ($i == 0 || $j == 0)
$LCSuff[$i][$j] = 0;
else if ($X[$i - 1] == $Y[$j - 1])
{
$LCSuff[$i][$j] = $LCSuff[$i - 1][$j - 1] + 1;
$result = max($result,
$LCSuff[$i][$j]);
}
else $LCSuff[$i][$j] = 0;
}
}
return $result;
}
// Driver Code
$X = "OldSite:GeeksforGeeks.org";
$Y = "NewSite:GeeksQuiz.com";
$m = strlen($X);
$n = strlen($Y);
echo "Length of Longest Common Substring is " .
LCSubStr($X, $Y, $m, $n);
// This code is contributed by ita_c
?>
Javascript
<script>
// JavaScript implementation of
// finding length of longest
// Common substring using
// Dynamic Programming
/*
Returns length of longest common
substring of X[0..m-1] and Y[0..n-1]
*/
function LCSubStr( X, Y , m , n) {
// Create a table to store
// lengths of longest common
// suffixes of substrings.
// Note that LCSuff[i][j]
// contains length of longest
// common suffix of
// X[0..i-1] and Y[0..j-1].
// The first row and first
// column entries have no
// logical meaning, they are
// used only for simplicity of program
var LCStuff =
Array(m + 1).fill().map(()=>Array(n + 1).fill(0));
// To store length of the longest
// common substring
var result = 0;
// Following steps build
// LCSuff[m+1][n+1] in bottom up fashion
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 || j == 0)
LCStuff[i][j] = 0;
else if (X[i - 1] == Y[j - 1]) {
LCStuff[i][j] = LCStuff[i - 1][j - 1] + 1;
result = Math.max(result, LCStuff[i][j]);
} else
LCStuff[i][j] = 0;
}
}
return result;
}
// Driver Code
var X = "OldSite:GeeksforGeeks.org";
var Y = "NewSite:GeeksQuiz.com";
var m = X.length;
var n = Y.length;
document.write("Length of Longest Common Substring is " +
LCSubStr(X, Y, m, n));
// This code contributed by Rajput-Ji
</script>
Length of Longest Common Substring is 10
Tiempo Complejidad: O(m*n)
Espacio Auxiliar: O(m*n)
Otro enfoque: (enfoque de espacio optimizado).
En el enfoque anterior, solo usamos la última fila de la array 2D, por lo que podemos optimizar el espacio usando
una array 2D de dimensión 2*(min(n,m)).
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to find the length of the
// longest LCS
int LCSubStr(string s, string t, int n, int m)
{
// Create DP table
int dp[2][m + 1];
int res = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (s[i - 1] == t[j - 1]) {
dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;
if (dp[i % 2][j] > res)
res = dp[i % 2][j];
}
else
dp[i % 2][j] = 0;
}
}
return res;
}
// Driver Code
int main()
{
string X = "OldSite:GeeksforGeeks.org";
string Y = "NewSite:GeeksQuiz.com";
int m = X.length();
int n = Y.length();
cout << LCSubStr(X, Y, m, n);
return 0;
cout << "GFG!";
return 0;
}
// This code is contributed by rajsanghavi9.
Java
// Java implementation of the above approach
class GFG
{
// Function to find the length of the
// longest LCS
static int LCSubStr(String s,String t,
int n,int m)
{
// Create DP table
int dp[][]=new int[2][m+1];
int res=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(s.charAt(i-1)==t.charAt(j-1))
{
dp[i%2][j]=dp[(i-1)%2][j-1]+1;
if(dp[i%2][j]>res)
res=dp[i%2][j];
}
else dp[i%2][j]=0;
}
}
return res;
}
// Driver Code
public static void main (String[] args)
{
String X="OldSite:GeeksforGeeks.org";
String Y="NewSite:GeeksQuiz.com";
int m=X.length();
int n=Y.length();
// Function call
System.out.println(LCSubStr(X,Y,m,n));
}
}
Python3
# Python implementation of the above approach # Function to find the length of the # longest LCS def LCSubStr(s, t, n, m): # Create DP table dp = [[0 for i in range(m + 1)] for j in range(2)] res = 0 for i in range(1,n + 1): for j in range(1,m + 1): if(s[i - 1] == t[j - 1]): dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1 if(dp[i % 2][j] > res): res = dp[i % 2][j] else: dp[i % 2][j] = 0 return res # Driver Code X = "OldSite:GeeksforGeeks.org" Y = "NewSite:GeeksQuiz.com" m = len(X) n = len(Y) # Function call print(LCSubStr(X,Y,m,n)) # This code is contributed by avanitrachhadiya2155
C#
// C# implementation of the above approach
using System;
public class GFG
{
// Function to find the length of the
// longest LCS
static int LCSubStr(string s,string t,
int n,int m)
{
// Create DP table
int[,] dp = new int[2, m + 1];
int res = 0;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
if(s[i - 1] == t[j - 1])
{
dp[i % 2, j] = dp[(i - 1) % 2, j - 1] + 1;
if(dp[i % 2, j] > res)
res = dp[i % 2, j];
}
else dp[i % 2, j] = 0;
}
}
return res;
}
// Driver Code
static public void Main (){
string X = "OldSite:GeeksforGeeks.org";
string Y = "NewSite:GeeksQuiz.com";
int m = X.Length;
int n = Y.Length;
// Function call
Console.WriteLine(LCSubStr(X,Y,m,n));
}
}
// This code is contributed by rag2127
Javascript
<script>
// JavaScript implementation of the above approach
// Function to find the length of the
// longest LCS
function LCSubStr(s, t, n, m)
{
// Create DP table
var dp = Array(2).fill().map(()=>Array(m+ 1).fill(0));
var res = 0;
for(var i = 1; i <= n; i++)
{
for(var j = 1; j <= m; j++)
{
if(s.charAt(i - 1) == t.charAt(j - 1))
{
dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;
if(dp[i % 2][j] > res)
res = dp[i % 2][j];
}
else dp[i % 2][j] = 0;
}
}
return res;
}
// Driver Code
var X = "OldSite:GeeksforGeeks.org";
var Y = "NewSite:GeeksQuiz.com";
var m = X.length;
var n = Y.length;
// Function call
document.write(LCSubStr(X, Y, m, n));
// This code is contributed by shivanisinghss2110
</script>
10
Complejidad temporal: O(n*m)
Espacio auxiliar: O(min(m,n))
Otro enfoque: (usando la recursividad)
Aquí está la solución recursiva del enfoque anterior.
C++
// C++ program using to find length of the
// longest common substring recursion
#include <iostream>
using namespace std;
string X, Y;
// Returns length of function f
// or longest common substring
// of X[0..m-1] and Y[0..n-1]
int lcs(int i, int j, int count)
{
if (i == 0 || j == 0)
return count;
if (X[i - 1] == Y[j - 1]) {
count = lcs(i - 1, j - 1, count + 1);
}
count = max(count,
max(lcs(i, j - 1, 0),
lcs(i - 1, j, 0)));
return count;
}
// Driver code
int main()
{
int n, m;
X = "abcdxyz";
Y = "xyzabcd";
n = X.size();
m = Y.size();
cout << lcs(n, m, 0);
return 0;
}
Java
// Java program using to find length of the
// longest common substring recursion
class GFG {
static String X, Y;
// Returns length of function
// for longest common
// substring of X[0..m-1] and Y[0..n-1]
static int lcs(int i, int j, int count)
{
if (i == 0 || j == 0)
{
return count;
}
if (X.charAt(i - 1)
== Y.charAt(j - 1))
{
count = lcs(i - 1, j - 1, count + 1);
}
count = Math.max(count,
Math.max(lcs(i, j - 1, 0),
lcs(i - 1, j, 0)));
return count;
}
// Driver code
public static void main(String[] args)
{
int n, m;
X = "abcdxyz";
Y = "xyzabcd";
n = X.length();
m = Y.length();
System.out.println(lcs(n, m, 0));
}
}
// This code is contributed by Rajput-JI
Python3
# Python3 program using to find length of # the longest common substring recursion # Returns length of function for longest # common substring of X[0..m-1] and Y[0..n-1] def lcs(i, j, count): if (i == 0 or j == 0): return count if (X[i - 1] == Y[j - 1]): count = lcs(i - 1, j - 1, count + 1) count = max(count, max(lcs(i, j - 1, 0), lcs(i - 1, j, 0))) return count # Driver code if __name__ == "__main__": X = "abcdxyz" Y = "xyzabcd" n = len(X) m = len(Y) print(lcs(n, m, 0)) # This code is contributed by Ryuga
C#
// C# program using to find length
// of the longest common substring
// recursion
using System;
class GFG {
static String X, Y;
// Returns length of function for
// longest common substring of
// X[0..m-1] and Y[0..n-1]
static int lcs(int i, int j, int count)
{
if (i == 0 || j == 0) {
return count;
}
if (X[i - 1] == Y[j - 1]) {
count = lcs(i - 1, j - 1, count + 1);
}
count = Math.Max(count, Math.Max(lcs(i, j - 1, 0),
lcs(i - 1, j, 0)));
return count;
}
// Driver code
public static void Main()
{
int n, m;
X = "abcdxyz";
Y = "xyzabcd";
n = X.Length;
m = Y.Length;
Console.Write(lcs(n, m, 0));
}
}
// This code is contributed by Rajput-JI
PHP
<?php
// PHP program using to find length of the
// longest common substring recursion
// Returns length of function for
// longest common substring of
// X[0..m-1] and Y[0..n-1]
function lcs($i, $j, $count, &$X, &$Y)
{
if ($i == 0 || $j == 0)
return $count;
if ($X[$i - 1] == $Y[$j - 1])
{
$count = lcs($i - 1, $j - 1,
$count + 1, $X, $Y);
}
$count = max($count, lcs($i, $j - 1, 0, $X, $Y),
lcs($i - 1, $j, 0, $X, $Y));
return $count;
}
// Driver code
$X = "abcdxyz";
$Y = "xyzabcd";
$n = strlen($X);
$m = strlen($Y);
echo lcs($n, $m, 0, $X, $Y);
// This code is contributed
// by rathbhupendra
?>
Javascript
<script>
// Javascript program using to find length of the
// longest common substring recursion
let X, Y;
// Returns length of function f
// or longest common substring
// of X[0..m-1] and Y[0..n-1]
function lcs(i, j, count)
{
if (i == 0 || j == 0)
return count;
if (X[i - 1] == Y[j - 1]) {
count = lcs(i - 1, j - 1, count + 1);
}
count = Math.max(count,
Math.max(lcs(i, j - 1, 0),
lcs(i - 1, j, 0)));
return count;
}
let n, m;
X = "abcdxyz";
Y = "xyzabcd";
n = X.length;
m = Y.length;
document.write(lcs(n, m, 0));
// This code is contributed by divyeshrabadiya07.
</script>
4
Optimización máxima del espacio :
- En este método, usaremos la recursividad para encontrar el prefijo más largo de todas las substrings posibles.
- Let
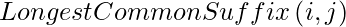 da la longitud del sufijo común más largo a partir de los índices i , j de strings X , Y respectivamente.
da la longitud del sufijo común más largo a partir de los índices i , j de strings X , Y respectivamente. - Entonces la función se puede definir como:
![Rendered by QuickLaTeX.com LongestCommonSuffix\left(i, j\right) = \begin{cases} 1 + LongestCommonSuffix\left(i + 1, j + 1\right) & \text{if} & 0 \le i \lt \left|X\right| & \text{and} & 0 \le j \lt \left|Y\right| & \text{and} & X\left[i\right] = Y\left[j\right] \\ 0 & \text{otherwise} \end{cases}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac1a1104d20022634330085207b2eb60_l3.png)
- En esta recursión podemos ver que la función tiene solo una dependencia, lo que significa que podemos memorizar solo el cálculo anterior si hacemos nuestro cálculo en un orden específico.
- Considere la siguiente tabla donde memorizamos las soluciones:
| 0 | 1 | 2 | 3 | 4 | |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 |
Necesitamos encontrar la solución en diagonal hacia arriba. En este ejemplo en particular:
- primera diagonal
- (4, 0)
- segunda diagonal
- (4, 1)
- (3, 0)
- tercera diagonal
- (4, 2)
- (3, 1)
- (2, 0)
- …
De esta manera, necesitamos recordar solo el cálculo anterior.
Python3
# Python code for the above approach
from functools import lru_cache
from operator import itemgetter
def longest_common_substring(x: str, y: str) -> (int, int, int):
# function to find the longest common substring
# Memorizing with maximum size of the memory as 1
@lru_cache(maxsize=1)
# function to find the longest common prefix
def longest_common_prefix(i: int, j: int) -> int:
if 0 <= i < len(x) and 0 <= j < len(y) and x[i] == y[j]:
return 1 + longest_common_prefix(i + 1, j + 1)
else:
return 0
# diagonally computing the subproblems
# to decrease memory dependency
def digonal_computation():
# upper right triangle of the 2D array
for k in range(len(x)):
yield from ((longest_common_prefix(i, j), i, j)
for i, j in zip(range(k, -1, -1),
range(len(y) - 1, -1, -1)))
# lower left triangle of the 2D array
for k in range(len(y)):
yield from ((longest_common_prefix(i, j), i, j)
for i, j in zip(range(k, -1, -1),
range(len(x) - 1, -1, -1)))
# returning the maximum of all the subproblems
return max(digonal_computation(), key=itemgetter(0), default=(0, 0, 0))
# Driver Code
if __name__ == '__main__':
x: str = 'GeeksforGeeks'
y: str = 'GeeksQuiz'
length, i, j = longest_common_substring(x, y)
print(f'length: {length}, i: {i}, j: {j}')
print(f'x substring: {x[i: i + length]}')
print(f'y substring: {y[j: j + length]}')
length: 5, i: 0, j: 0 x substring: Geeks y substring: Geeks
Complejidad de tiempo : ![]()
Complejidad de espacio : ![]()
Ejercicio: La solución anterior imprime solo la longitud de la substring común más larga. Extienda la solución para imprimir también la substring.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA