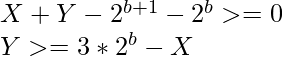Suma de AND bit a bit de suma de pares y su AND bit a bit de una array dada

Dada una array arr[] que consta de N enteros, la tarea es encontrar la suma de Bitwise AND de (arr[i] + arr[j]) y Bitwise AND de arr[i] y arr[j] para cada par de elementos (arr[i], arr[j]) de la array dada. Como la suma puede ser muy grande, imprímela módulo (10 ⁹ + 7) .

Ejemplos:

Entrada: arr[] = {8, 9}
Salida: 0
Explicación: El único par de la array es (8, 9). Suma del par = (8 + 9) = 17. Y bit a bit de los pares = (8 y 9) = 8. Por lo tanto, se requiere AND bit a bit = (17 y 8) = 0.

Entrada: arr[] = {1, 3, 3}
Salida: 2
Explicación:
Par (1, 3): Obligatorio Bit a bit AND = (1 + 3) & (1 & 3) = (4 & 1) = 0.
Par (3, 3): Obligatorio Bitwise AND = (3 + 3) & (3 & 3) = (6 & 3) = 2.
Por lo tanto, la suma total = 0 + 0 + 2 = 2.

Enfoque ingenuo: el enfoque más simple es generar todos los pares posibles a partir de la array dada y verificar si existe algún par que satisfaga la condición dada o no. Si se encuentra que es cierto, entonces cuente este par. Después de verificar todos los pares, imprima el conteo resultante . 
Complejidad de Tiempo: O(N ² )
Espacio Auxiliar: O(1)

Enfoque eficiente: el enfoque anterior se puede optimizar en función de las siguientes observaciones:

• Teniendo en cuenta el par (X, Y) , el AND a nivel de bits en un bit, digamos que b ^th es 1 , entonces (X + Y) también debe tener el b ^th bit como un bit establecido para contribuir en el b ^th bit.
• Considerando sólo los últimos b bits de ambos números de dichos pares, se puede observar que para satisfacer la condición anterior, b ^-ésimo bit y (b + 1) ^-ésimo bit, ambos deberán establecerse.
• Por lo tanto, de los pasos anteriores, se puede deducir que para satisfacer las condiciones anteriores, se debe cumplir la siguiente condición:

• Por lo tanto, la tarea se reduce a encontrar el conteo de pares que satisfacen la condición anterior para cada posición de bit e incrementar el resultado por el valor cnt*2 ^b  para 0 ≤ b < 31 .

Siga los pasos a continuación para resolver el problema:

• Inicialice una variable, digamos ans , para almacenar la suma resultante.
• Itere sobre el rango [0, 30] y realice las siguientes operaciones:
  • Inicialice un vector V que almacene los pares que cumplan las condiciones anteriores.
  • Recorra la array dada arr[] e inserte el valor arr[j] – (arr[j] >> (i + 1))*(1 << (i + 1)) módulo M en el vector V , si (( arr[j] >> (i + 1)) &1) es verdadero.
  • Ordena el vector V en orden ascendente .
  • Recorra el vector V y realice lo siguiente:
    • Calcule el valor 2 ^{(i + 1)} + 2 ⁱ – V[j] y guárdelo en una variable, digamos Y .
    • Encuentra el número de puntos en V que es mayor o igual que Y en V y guárdalo en una variable, digamos cnt , es decir, cnt = V.size() – (lower_bound(V.begin() + j + 1, V.end(), Y) – V.begin()).
    • Actualice el ans como ans = (ans+ cnt* 2 ⁱ )%M .
• Después de completar los pasos anteriores, imprima el valor de ans como resultado.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
 
#include <bits/stdc++.h>
#define M 1000000007
using namespace std;
 
// Function to find the sum of Bitwise AND
// of sum of pairs and their Bitwise AND
// from a given array
void findSum(int A[], int N)
{
    // Stores the total sum
    long long ans = 0;
 
    for (int i = 0; i < 30; i++) {
 
        vector<long long> vec;
 
        for (int j = 0; j < N; j++) {
 
            // Check if jth bit is set
            if ((A[j] >> i) & 1) {
 
                // Stores the right shifted
                // element by(i+1)
                long long X = (A[j] >> (i + 1));
 
                // Update the value
                // of X
                X = X * (1 << (i + 1));
                X %= M;
 
                // Push in vector vec
                vec.push_back(A[j] - X);
            }
        }
        // Sort the vector in
        // ascending order
        sort(vec.begin(), vec.end());
 
        // Traverse the vector vec
        for (int j = 0; j < vec.size(); j++) {
 
            // Stores the value
            // 2^(i+1)- 2^(i)- vec[j]
            int Y = (1 << (i + 1))
                    + (1 << i)
                    - vec[j];
 
            // Stores count of numbers
            // whose value > Y
            int idx = lower_bound(
                          vec.begin() + j + 1,
                          vec.end(), Y)
                      - vec.begin();
 
            // Update the ans
            ans += (vec.size() - idx)
                   * 1ll * (1 << i);
 
            ans %= M;
        }
    }
 
    // Return the ans
    cout << ans % M << endl;
}
 
// Driver Code
int main()
{
    int arr[] = { 1, 3, 3 };
    int N = sizeof(arr) / sizeof(arr[0]);
    findSum(arr, N);
 
    return 0;
}

# Python 3 program for the above approach
M = 1000000007
from bisect import bisect_left
 
# Function to find the sum of Bitwise AND
# of sum of pairs and their Bitwise AND
# from a given array
def findSum(A, N):
   
    # Stores the total sum
    ans = 0
 
    for i in range(30):
        vec = []
 
        for j in range(N):
            # Check if jth bit is set
            if ((A[j] >> i) & 1):
                # Stores the right shifted
                # element by(i+1)
                X = (A[j] >> (i + 1))
 
                # Update the value
                # of X
                X = X * (1 << (i + 1))
                X %= M
 
                # Push in vector vec
                vec.append(A[j] - X)
 
        # Sort the vector in
        # ascending order
        vec.sort(reverse=False)
 
        # Traverse the vector vec
        for j in range(len(vec)):
           
            # Stores the value
            # 2^(i+1)- 2^(i)- vec[j]
            Y = (1 << (i + 1)) + (1 << i) - vec[j]
 
            # Stores count of numbers
            # whose value > Y
            temp = vec[j+1:]
            idx = int(bisect_left(temp,Y))
 
            # Update the ans
            ans += ((len(vec) - idx) * (1 << i))
 
            ans %= M
    ans /= 7
 
    # Return the ans
    print(int(ans % M))
 
# Driver Code
if __name__ == '__main__':
    arr =  [1, 3, 3]
    N = len(arr)
    findSum(arr, N)
 
    # This code is contributed by SURENNDRA_GANGWAR.

2

Complejidad de tiempo: O(N*log N)
Espacio auxiliar: O(N)