Dado un árbol de búsqueda binario y un número N, la tarea es encontrar la suma de los primos del Node N dado si un Node con el valor dado ‘N’ está presente en el BST dado; de lo contrario, imprima -1.
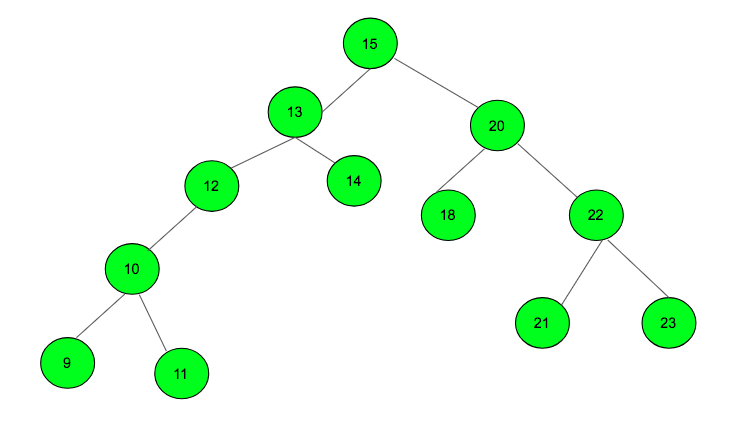
Ejemplos:
Input: Node = 12 Output: 40 Cousins are 18 and 22 Input: 19 Output: -1
Enfoque: A continuación se muestra el algoritmo para resolver el problema.
- Encuentre el padre del Node dado, si el Node no está presente, devuelva -1.
- Traverse en el árbol, encontrar el nivel de cada Node durante el recorrido.
- Si el nivel es el mismo que el Node dado. Verifique el padre de ese Node, si el padre es diferente, agregue el Node a la suma.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find the sum of cousins
// of a node of a given BST
#include <bits/stdc++.h>
using namespace std;
// structure to store the binary tree
struct Tree {
int data;
struct Tree *left, *right;
};
// insertion of node in the binary tree
struct Tree* newNode(int data)
{
// allocates memory
struct Tree* node = (struct Tree*)malloc(sizeof(struct Tree));
// initializes data
node->data = data;
// marks the left and right
// child as NULL
node->left = node->right = NULL;
// Return the node after allocating memory
return (node);
};
// Function which calculates the sum of the cousin Node
int SumOfCousin(struct Tree* root, int p,
int level1, int level)
{
int sum = 0;
if (root == NULL)
return 0;
// nodes which has same parent
// as the given node will not be
// taken to count for calculation
if (p == root->data)
return 0;
// if the level is same
// then it is a cousin
// as parent checking has been
// done above
if (level1 == level)
return root->data;
// traverse in the tree left and right
else
sum += SumOfCousin(root->left, p, level1 + 1, level) + SumOfCousin(root->right, p, level1 + 1, level);
return sum;
}
// Function that returns the parent node
int ParentNode(struct Tree* root, int NodeData)
{
int parent = -1;
// traverse the full Binary tree
while (root != NULL) {
// if node is found
if (NodeData == root->data)
break;
// if less than move to left
else if (NodeData < root->data) {
parent = root->data;
root = root->left;
}
// if greater than move to right
else {
parent = root->data;
root = root->right;
}
}
// Node not found
if (root == NULL)
return -1;
else
return parent;
}
// Function to find the level of the given node
int LevelOfNode(struct Tree* root, int NodeData)
{
// calculate the level of node
int level = 0;
while (root != NULL) {
// if the node is found
if (NodeData == root->data)
break;
// move to the left of the tree
if (NodeData < root->data) {
root = root->left;
}
// move to the right of the tree
else {
root = root->right;
}
// increase the level after every traversal
level++;
}
// return the level of a given node
return level;
}
// Driver Code
int main()
{
// initialize the root as NULL
struct Tree* root = NULL;
// Inserts node in the tree
// tree is the same as the one in image
root = newNode(15);
root->left = newNode(13);
root->left->left = newNode(12);
root->left->right = newNode(14);
root->right = newNode(20);
root->right->left = newNode(18);
root->right->right = newNode(22);
// Given Node
int NodeData = 12;
int p, level, sum;
// function call to find the parent node
p = ParentNode(root, NodeData);
// if given Node is not present then print -1
if (p == -1)
cout << "-1\n";
// if present then find the level of the node
// and call the sum of cousin function
else {
// function call to find the level of that node
level = LevelOfNode(root, NodeData);
// sum of cousin nodes of the given nodes
sum = SumOfCousin(root, p, 0, level);
// print the sum
cout << sum;
}
return 0;
}
Java
// Java program to find the sum of cousins
// of a node of a given BST
class GFG
{
// structure to store the binary tree
static class Tree
{
int data;
Tree left, right;
};
// insertion of node in the binary tree
static Tree newNode(int data)
{
// allocates memory
Tree node = new Tree();
// initializes data
node.data = data;
// marks the left and right
// child as null
node.left = node.right = null;
// Return the node after allocating memory
return (node);
}
// Function which calculates
// the sum of the cousin Node
static int SumOfCousin(Tree root, int p,
int level1, int level)
{
int sum = 0;
if (root == null)
return 0;
// nodes which has same parent
// as the given node will not be
// taken to count for calculation
if (p == root.data)
return 0;
// if the level is same
// then it is a cousin
// as parent checking has been
// done above
if (level1 == level)
return root.data;
// traverse in the tree left and right
else
sum += SumOfCousin(root.left, p, level1 + 1, level) +
SumOfCousin(root.right, p, level1 + 1, level);
return sum;
}
// Function that returns the parent node
static int ParentNode(Tree root, int NodeData)
{
int parent = -1;
// traverse the full Binary tree
while (root != null)
{
// if node is found
if (NodeData == root.data)
break;
// if less than move to left
else if (NodeData < root.data)
{
parent = root.data;
root = root.left;
}
// if greater than move to right
else
{
parent = root.data;
root = root.right;
}
}
// Node not found
if (root == null)
return -1;
else
return parent;
}
// Function to find the level of the given node
static int LevelOfNode(Tree root, int NodeData)
{
// calculate the level of node
int level = 0;
while (root != null)
{
// if the node is found
if (NodeData == root.data)
break;
// move to the left of the tree
if (NodeData < root.data)
{
root = root.left;
}
// move to the right of the tree
else
{
root = root.right;
}
// increase the level after every traversal
level++;
}
// return the level of a given node
return level;
}
// Driver Code
public static void main(String[] args)
{
// initialize the root as null
Tree root = null;
// Inserts node in the tree
// tree is the same as the one in image
root = newNode(15);
root.left = newNode(13);
root.left.left = newNode(12);
root.left.right = newNode(14);
root.right = newNode(20);
root.right.left = newNode(18);
root.right.right = newNode(22);
// Given Node
int NodeData = 12;
int p, level, sum;
// function call to find the parent node
p = ParentNode(root, NodeData);
// if given Node is not present then print -1
if (p == -1)
System.out.print("-1\n");
// if present then find the level of the node
// and call the sum of cousin function
else
{
// function call to find the level of that node
level = LevelOfNode(root, NodeData);
// sum of cousin nodes of the given nodes
sum = SumOfCousin(root, p, 0, level);
// print the sum
System.out.print(sum);
}
}
}
// This code is contributed by 29AjayKumar
Python3
# Python3 program to find the sum of cousins
# of a node of a given BST
# structure to store the binary tree
class newNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Function which calculates the
# sum of the cousin Node
def SumOfCousin(root, p, level1, level):
sum = 0
if (root == None):
return 0
# Nodes which has same parent
# as the given node will not be
# taken to count for calculation
if (p == root.data):
return 0
# If the level is same
# then it is a cousin
# as parent checking has been
# done above
if (level1 == level):
return root.data
# Traverse in the tree left and right
else:
sum += (SumOfCousin(root.left, p,
level1 + 1, level) +
SumOfCousin(root.right, p,
level1 + 1, level))
return sum
# Function that returns the parent node
def ParentNode(root, NodeData):
parent = -1
# Traverse the full Binary tree
while (root != None):
# If node is found
if (NodeData == root.data):
break
# If less than move to left
elif (NodeData < root.data):
parent = root.data
root = root.left
# If greater than move to right
else:
parent = root.data
root = root.right
# Node not found
if (root == None):
return -1
else:
return parent
# Function to find the level of
# the given node
def LevelOfNode(root, NodeData):
# Calculate the level of node
level = 0
while (root != None):
# If the node is found
if (NodeData == root.data):
break
# Move to the left of the tree
if (NodeData < root.data):
root = root.left
# Move to the right of the tree
else:
root = root.right
# Increase the level after every traversal
level += 1
# Return the level of a given node
return level
# Driver Code
if __name__ == '__main__':
# Initialize the root as NULL
root = None
# Inserts node in the tree
# tree is the same as the
# one in image
root = newNode(15)
root.left = newNode(13)
root.left.left = newNode(12)
root.left.right = newNode(14)
root.right = newNode(20)
root.right.left = newNode(18)
root.right.right = newNode(22)
# Given Node
NodeData = 12
# Function call to find the parent node
p = ParentNode(root, NodeData)
# If given Node is not present then print -1
if (p == -1):
print("-1")
# If present then find the level of the node
# and call the sum of cousin function
else:
# Function call to find the
# level of that node
level = LevelOfNode(root, NodeData)
# Sum of cousin nodes of the given nodes
sum = SumOfCousin(root, p, 0, level)
# Print the sum
print(sum)
# This code is contributed by bgangwar59
C#
// C# program to find the sum of cousins
// of a node of a given BST
using System;
class GFG
{
// structure to store the binary tree
class Tree
{
public int data;
public Tree left, right;
};
// insertion of node in the binary tree
static Tree newNode(int data)
{
// allocates memory
Tree node = new Tree();
// initializes data
node.data = data;
// marks the left and right
// child as null
node.left = node.right = null;
// Return the node after allocating memory
return (node);
}
// Function which calculates
// the sum of the cousin Node
static int SumOfCousin(Tree root, int p,
int level1, int level)
{
int sum = 0;
if (root == null)
return 0;
// nodes which has same parent
// as the given node will not be
// taken to count for calculation
if (p == root.data)
return 0;
// if the level is same
// then it is a cousin
// as parent checking has been
// done above
if (level1 == level)
return root.data;
// traverse in the tree left and right
else
sum += SumOfCousin(root.left, p,
level1 + 1, level) +
SumOfCousin(root.right, p,
level1 + 1, level);
return sum;
}
// Function that returns the parent node
static int ParentNode(Tree root,
int NodeData)
{
int parent = -1;
// traverse the full Binary tree
while (root != null)
{
// if node is found
if (NodeData == root.data)
break;
// if less than move to left
else if (NodeData < root.data)
{
parent = root.data;
root = root.left;
}
// if greater than move to right
else
{
parent = root.data;
root = root.right;
}
}
// Node not found
if (root == null)
return -1;
else
return parent;
}
// Function to find the level of the given node
static int LevelOfNode(Tree root, int NodeData)
{
// calculate the level of node
int level = 0;
while (root != null)
{
// if the node is found
if (NodeData == root.data)
break;
// move to the left of the tree
if (NodeData < root.data)
{
root = root.left;
}
// move to the right of the tree
else
{
root = root.right;
}
// increase the level
// after every traversal
level++;
}
// return the level of a given node
return level;
}
// Driver Code
public static void Main(String[] args)
{
// initialize the root as null
Tree root = null;
// Inserts node in the tree
// tree is the same as the one in image
root = newNode(15);
root.left = newNode(13);
root.left.left = newNode(12);
root.left.right = newNode(14);
root.right = newNode(20);
root.right.left = newNode(18);
root.right.right = newNode(22);
// Given Node
int NodeData = 12;
int p, level, sum;
// function call to find the parent node
p = ParentNode(root, NodeData);
// if given Node is not present
// then print -1
if (p == -1)
Console.Write("-1\n");
// if present then find the level of the node
// and call the sum of cousin function
else
{
// function call to find the level of that node
level = LevelOfNode(root, NodeData);
// sum of cousin nodes of the given nodes
sum = SumOfCousin(root, p, 0, level);
// print the sum
Console.Write(sum);
}
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// Javascript program to find the sum of
// cousins of a node of a given BST
// Structure to store the binary tree
class Tree
{
constructor(data)
{
this.left = null;
this.right = null;
this.data = data;
}
}
// Insertion of node in the binary tree
function newNode(data)
{
// Allocates memory
let node = new Tree(data);
// Return the node after
// allocating memory
return (node);
}
// Function which calculates
// the sum of the cousin Node
function SumOfCousin(root, p, level1, level)
{
let sum = 0;
if (root == null)
return 0;
// Nodes which has same parent
// as the given node will not be
// taken to count for calculation
if (p == root.data)
return 0;
// If the level is same
// then it is a cousin
// as parent checking has been
// done above
if (level1 == level)
return root.data;
// Traverse in the tree left and right
else
sum += SumOfCousin(root.left, p,
level1 + 1, level) +
SumOfCousin(root.right, p,
level1 + 1, level);
return sum;
}
// Function that returns the parent node
function ParentNode(root, NodeData)
{
let parent = -1;
// Traverse the full Binary tree
while (root != null)
{
// If node is found
if (NodeData == root.data)
break;
// If less than move to left
else if (NodeData < root.data)
{
parent = root.data;
root = root.left;
}
// If greater than move to right
else
{
parent = root.data;
root = root.right;
}
}
// Node not found
if (root == null)
return -1;
else
return parent;
}
// Function to find the level of the given node
function LevelOfNode(root, NodeData)
{
// Calculate the level of node
let level = 0;
while (root != null)
{
// If the node is found
if (NodeData == root.data)
break;
// Move to the left of the tree
if (NodeData < root.data)
{
root = root.left;
}
// Move to the right of the tree
else
{
root = root.right;
}
// Increase the level
// after every traversal
level++;
}
// Return the level of a given node
return level;
}
// Driver code
// Initialize the root as null
let root = null;
// Inserts node in the tree
// tree is the same as the one in image
root = newNode(15);
root.left = newNode(13);
root.left.left = newNode(12);
root.left.right = newNode(14);
root.right = newNode(20);
root.right.left = newNode(18);
root.right.right = newNode(22);
// Given Node
let NodeData = 12;
let p, level, sum;
// Function call to find the parent node
p = ParentNode(root, NodeData);
// If given Node is not present
// then print -1
if (p == -1)
document.write("-1" + "</br>");
// If present then find the level of the node
// and call the sum of cousin function
else
{
// Function call to find the level of that node
level = LevelOfNode(root, NodeData);
// Sum of cousin nodes of the given nodes
sum = SumOfCousin(root, p, 0, level);
// Print the sum
document.write(sum);
}
// This code is contributed by divyeshrabadiya07
</script>
Producción:
40
Publicación traducida automáticamente
Artículo escrito por Mohd_Saliem y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA