Dado un árbol binario y un número, devuelve verdadero si el árbol tiene una ruta de raíz a hoja tal que la suma de todos los valores a lo largo de la ruta es igual al número dado. Devuelve falso si no se puede encontrar dicha ruta.
C++
#include <bits/stdc++.h>
using namespace std;
#define bool int
/* A binary tree node has data, pointer to left child
and a pointer to right child */
class node
{
public:
int data;
node* left;
node* right;
};
/*
Given a tree and a sum, return true if there is a path from the root
down to a leaf, such that adding up all the values along the path
equals the given sum.
Strategy: subtract the node value from the sum when recurring down,
and check to see if the sum is 0 when you when you reach the leaf node.
*/
bool hasPathSum(node* Node, int sum)
{
if(Node==NULL)
return 0;
bool ans = 0;
int subSum = sum - Node->data;
/* If we reach a leaf node and sum becomes 0 then return true*/
if ( subSum == 0 && Node->left == NULL && Node->right == NULL )
return 1;
/* otherwise check both subtrees */
if(Node->left)
ans = ans || hasPathSum(Node->left, subSum);
if(Node->right)
ans = ans || hasPathSum(Node->right, subSum);
return ans;
}
/* UTILITY FUNCTIONS */
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
node* newnode(int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return(Node);
}
// Driver Code
int main()
{
int sum = 21;
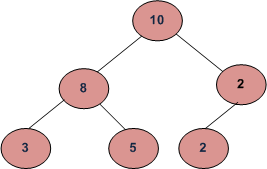
/* Constructed binary tree is
10
/ \
8 2
/ \ /
3 5 2
*/
node *root = newnode(10);
root->left = newnode(8);
root->right = newnode(2);
root->left->left = newnode(3);
root->left->right = newnode(5);
root->right->left = newnode(2);
if(hasPathSum(root, sum))
cout << "There is a root-to-leaf path with sum " << sum;
else
cout << "There is no root-to-leaf path with sum " << sum;
return 0;
}
// This code is contributed by rathbhupendra
C
#include <stdio.h>
#include <stdlib.h>
#define bool int
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
/*
Given a tree and a sum, return
true if there is a path from
the root down to a leaf, such
that adding up all the values
along the path equals the given sum.
Strategy: subtract the node
value from the sum when
recurring down, and check to
see if the sum is 0 when you reach the leaf node.
*/
bool hasPathSum(struct node* node, int sum)
{
if(node==NULL)
return 0;
bool ans = 0;
int subSum = sum - node->data;
/* If we reach a leaf node
and sum becomes 0 then
* return true*/
if (subSum == 0 && node->left == NULL
&& node->right == NULL)
return 1;
/* otherwise check both subtrees */
if (node->left)
ans = ans
|| hasPathSum(node->left, subSum);
if (node->right)
ans = ans
|| hasPathSum(node->right, subSum);
return ans;
}
/* UTILITY FUNCTIONS */
/* Helper function that
allocates a new node with the
given data and NULL left
and right pointers. */
struct node* newnode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
// Driver Code
int main()
{
int sum = 21;
/* Constructed binary tree is
10
/ \
8 2
/ \ /
3 5 2
*/
struct node* root = newnode(10);
root->left = newnode(8);
root->right = newnode(2);
root->left->left = newnode(3);
root->left->right = newnode(5);
root->right->left = newnode(2);
if (hasPathSum(root, sum))
printf("There is a root-to-leaf path with sum %d",
sum);
else
printf("There is no root-to-leaf path with sum %d",
sum);
getchar();
return 0;
}
Java
// Java program to print
// root to leaf path sum
// equal to a given number
/* A binary tree node has data,
pointer to left child
and a pointer to right child */
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree {
Node root;
/*
Given a tree and a sum,
return true if there is a path
from the root down to a leaf,
such that adding up all
the values along the path
equals the given sum.
Strategy: subtract the node
value from the sum when
recurring down, and check to
see if the sum is 0 you reach the leaf node.
*/
boolean hasPathSum(Node node, int sum)
{ /* If the tree is empty there is no way the reqd sum will be there. */
if(root==null)
return false;
boolean ans = false;
int subSum = sum - node.data;
if(subSum == 0 && node.left == null && node.right == null)
return(ans = true);
if(node.left != null)
// ans || hasPathSum... has no utility if the ans is false
ans = ans || hasPathSum(node.left, subSum);
if(node.right != null)
// But if it is true then we can avoid calling hasPathSum
// here as answer has already been found
ans = ans || hasPathSum(node.right, subSum);
return(ans);
}
// Driver Code
public static void main(String args[])
{
int sum = 21;
/* Constructed binary tree is
10
/ \
8 2
/ \ /
3 5 2
*/
BinaryTree tree = new BinaryTree();
tree.root = new Node(10);
tree.root.left = new Node(8);
tree.root.right = new Node(2);
tree.root.left.left = new Node(3);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(2);
if (tree.hasPathSum(tree.root, sum))
System.out.println(
"There is a root to leaf path with sum "
+ sum);
else
System.out.println(
"There is no root to leaf path with sum "
+ sum);
}
}
// This code has been contributed by Mayank
// Jaiswal(mayank_24)
Python3
# Python program to find if
# there is a root to sum path
# A binary tree node
class Node:
# Constructor to create a new node
def __init__(self, data):
self.data = data
self.left = None
self.right = None
"""
Given a tree and a sum, return
true if there is a path from the root
down to a leaf, such that
adding up all the values along the path
equals the given sum.
Strategy: subtract the node
value from the sum when recurring down,
and check to see if the sum
is 0 when you run out of tree.
"""
# s is the sum
def hasPathSum(node, s):
ans = 0
subSum = s - node.data
# If we reach a leaf node and sum becomes 0, then
# return True
if(subSum == 0 and node.left == None and node.right == None):
return True
# Otherwise check both subtrees
if node.left is not None:
ans = ans or hasPathSum(node.left, subSum)
if node.right is not None:
ans = ans or hasPathSum(node.right, subSum)
return ans
# Driver Code
s = 21
root = Node(10)
root.left = Node(8)
root.right = Node(2)
root.left.right = Node(5)
root.left.left = Node(3)
root.right.left = Node(2)
if hasPathSum(root, s):
print("There is a root-to-leaf path with sum %d" % (s))
else:
print("There is no root-to-leaf path with sum %d" % (s))
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
// C# program to print root to
// leaf path sum equal to a given number
using System;
/* A binary tree node has data, pointer
to left child and a pointer to right child */
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
class GFG {
public Node root;
/*
Given a tree and a sum, return true if
there is a path from the root down to a
leaf, such that adding up all the values
along the path equals the given sum.
Strategy: subtract the node value from the
sum when recurring down, and check to see
if the sum is 0 when you you reach the leaf node..
*/
public virtual bool haspathSum(Node node, int sum)
{
ans = false;
int subsum = sum - node.data;
if (subsum == 0 && node.left == null
&& node.right == null) {
return true;
}
/* otherwise check both subtrees */
if (node.left != null) {
ans = ans || haspathSum(node.left, subsum);
}
if (node.right != null) {
ans = ans || haspathSum(node.right, subsum);
}
return ans;
}
// Driver Code
public static void Main(string[] args)
{
int sum = 21;
/* Constructed binary tree is
10
/ \
8 2
/ \ /
3 5 2
*/
GFG tree = new GFG();
tree.root = new Node(10);
tree.root.left = new Node(8);
tree.root.right = new Node(2);
tree.root.left.left = new Node(3);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(2);
if (tree.haspathSum(tree.root, sum)) {
Console.WriteLine("There is a root to leaf "
+ "path with sum " + sum);
}
else {
Console.WriteLine("There is no root to leaf "
+ "path with sum " + sum);
}
}
}
// This code is contributed by Shrikant13
Javascript
<script>
// javascript program to print
// root to leaf path sum
// equal to a given number
/* A binary tree node has data,
pointer to left child
and a pointer to right child */
class Node {
constructor(val) {
this.data = val;
this.left = null;
this.right = null;
}
}
var root;
/*
Given a tree and a sum,
return true if there is a path
from the root down to a leaf,
such that adding up all
the values along the path
equals the given sum.
Strategy: subtract the node
value from the sum when
recurring down, and check to
see if the sum is 0 you reach the leaf node.
*/
function hasPathSum(node , sum)
{
var ans = false;
var subSum = sum - node.data;
if(subSum == 0 && node.left == null && node.right == null)
return(ans = true);
if(node.left != null)
// ans || hasPathSum... has no utility if the ans is false
ans = ans || hasPathSum(node.left, subSum);
if(node.right != null)
// But if it is true then we can afunction calling hasPathSum
// here as answer has already been found
ans = ans || hasPathSum(node.right, subSum);
return(ans);
}
// Driver Code
var sum = 21;
/* Constructed binary tree is
10
/ \
8 2
/ \ /
3 5 2
*/
var root = new Node(10);
root.left = new Node(8);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(5);
root.right.left = new Node(2);
if (hasPathSum(root, sum))
document.write(
"There is a root to leaf path with sum "
+ sum);
else
document.write(
"There is no root to leaf path with sum "
+ sum);
// This code is contributed by gauravrajput1
</script>
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA