Dado un gráfico no cíclico que tiene V Nodes y E aristas y un Node fuente S , la tarea es calcular la suma del elemento mínimo en cada nivel del Node fuente S en el gráfico dado.
Ejemplos:
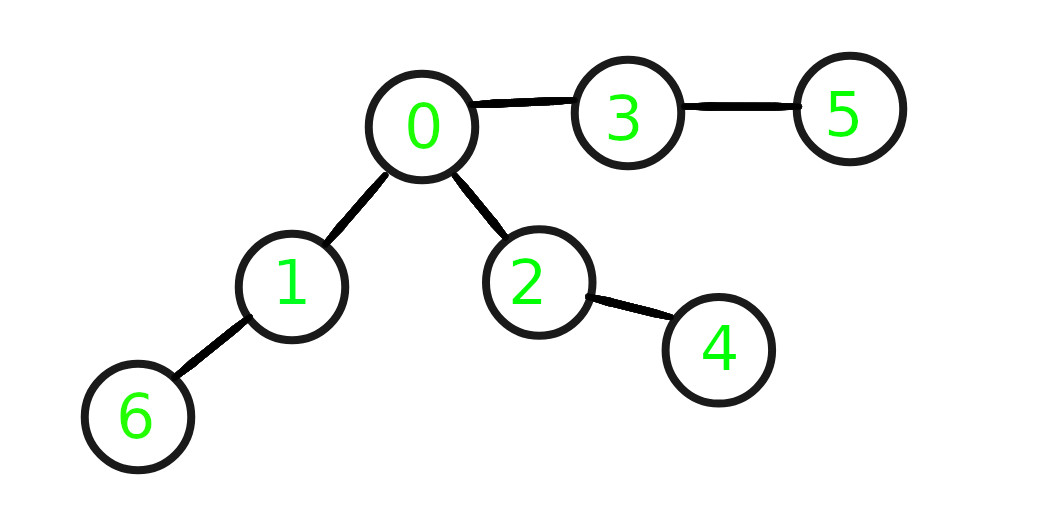
Entrada: S = 0, a continuación se muestra el gráfico dado
Salida: 5
Explicación:
Solo hay un Node en la profundidad 0, es decir, 0.
En la profundidad 1, hay 3 Nodes 1, 2, 3, y el mínimo de ellos es 1.
En la profundidad 2, hay otros 3 Nodes, es decir, 6, 4, 5 , y un mínimo de ellos es 4.
Entonces, la suma del elemento mínimo en cada profundidad es 0 + 1 + 4 = 5.
Ingrese: S = 2, a continuación se muestra el gráfico dado
Salida: 8
Explicación:
En la profundidad 0 solo existe 1 Node, es decir, 2.
En la profundidad 1, el elemento mínimo es 0.
En la profundidad 2, el elemento mínimo es 1.
En la profundidad 3, el elemento mínimo es 5
Entonces, la suma del elemento mínimo en cada profundidad es 2 + 0 + 1 + 5 = 8.
Enfoque: La idea es utilizar DFS Traversal . A continuación se muestran los pasos:
- Inicialice una array (digamos arr[] ) para almacenar el elemento mínimo en cada nivel.
- Inicie el DFS Traversal desde el Node de origen dado S con una profundidad variable (inicialmente 0 ).
- Actualice el valor mínimo de la profundidad actual en la array arr[] .
- Se recurre recursivamente para el Node secundario incrementando el valor de profundidad de la llamada recursiva anterior de modo que el valor mínimo en la profundidad correspondiente se pueda actualizar en consecuencia.
- Después de los pasos anteriores, la suma de los valores almacenados en arr[] es la suma total requerida.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to add an edge in a graph
void addEdge(vector<int> adj[],
int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
// Variable to store depth of graph
int max_depth = 0;
// Function to know the depth of graph
void find_depth(vector<int> adj[],
vector<bool>& visited,
int start, int depth)
{
// Mark the node start as true
visited[start] = true;
// Update the maximum depth
max_depth = max(max_depth, depth);
// Recurr for the child node of
// start node
for (auto i : adj[start]) {
if (!visited[i])
find_depth(adj, visited,
i, depth + 1);
}
}
// Function to calculate min value
// at every depth
void dfs(vector<int> adj[], int start,
vector<bool>& visited,
vector<int>& store_min_elements,
int depth)
{
// marking already visited
// vertices as true
visited[start] = true;
// Store the min value for
// every depth
store_min_elements[depth]
= min(store_min_elements[depth],
start);
// Traverse Child node of start node
for (auto i : adj[start]) {
if (!visited[i])
dfs(adj, i, visited,
store_min_elements,
depth + 1);
}
}
// Function to calculate the sum
void minSum_depth(vector<int> adj[],
int start,
int total_nodes)
{
vector<bool> visited(total_nodes,
false);
// Calling function to know
// the depth of graph
find_depth(adj, visited,
start, 0);
// Set all value of visited
// to false again
fill(visited.begin(),
visited.end(), false);
// Declaring vector of
// "max_depth + 1" size to
// store min values at every
// depth initialise vector
// with max number
vector<int> store_min_elements(
max_depth + 1, INT_MAX);
// Calling dfs function for
// calculation of min element
// at every depth
dfs(adj, start, visited,
store_min_elements, 0);
// Variable to store sum of
// all min elements
int min_sum = 0;
// Calculation of minimum sum
for (int i = 0;
i < store_min_elements.size();
i++) {
min_sum += store_min_elements[i];
}
// Print the minimum sum
cout << min_sum << endl;
}
// Driver Code
int main()
{
// Given Nodes and start node
int V = 7, start = 0;
// Given graph
vector<int> adj[V];
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 0, 3);
addEdge(adj, 1, 6);
addEdge(adj, 2, 4);
addEdge(adj, 3, 5);
// Function Call
minSum_depth(adj, start, V);
}
Java
// Java program for the above approach
import java.io.*;
import java.util.*;
class Graph{
public static int V;
// Variable to store depth of graph
public static int max_depth = 0;
private static LinkedList<Integer> adj[];
@SuppressWarnings("unchecked")
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for(int i = 0; i < v; ++i)
adj[i] = new LinkedList();
}
static void addEdge(int v, int w)
{
adj[v].add(w);
}
static void find_depth(boolean visited[],
int start, int depth)
{
// Mark the node start as true
visited[start] = true;
// Update the maximum depth
max_depth = Math.max(max_depth, depth);
// Recurr for the child node of
// start node
Iterator<Integer> i = adj[start].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
find_depth(visited, n, depth + 1);
}
}
// Function to calculate min value
// at every depth
static void dfs(int start, boolean visited[],
int store_min_elements[],
int depth)
{
// Marking already visited
// vertices as true
visited[start] = true;
// Store the min value for
// every depth
store_min_elements[depth] = Math.min(
store_min_elements[depth], start);
// Traverse Child node of start node
Iterator<Integer> i = adj[start].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
dfs(n, visited, store_min_elements,
depth + 1);
}
}
// Function to calculate the sum
static void minSum_depth(int start, int total_nodes)
{
boolean visited[] = new boolean[total_nodes];
// Calling function to know
// the depth of graph
find_depth(visited, start, 0);
// Set all value of visited
// to false again
Arrays.fill(visited, false);
// Declaring vector of
// "max_depth + 1" size to
// store min values at every
// depth initialise vector
// with max number
int store_min_elements[] = new int[max_depth + 1];
Arrays.fill(store_min_elements,
Integer.MAX_VALUE);
// Calling dfs function for
// calculation of min element
// at every depth
dfs(start, visited,
store_min_elements, 0);
// Variable to store sum of
// all min elements
int min_sum = 0;
// Calculation of minimum sum
for(int i = 0;
i < store_min_elements.length;
i++)
{
min_sum += store_min_elements[i];
}
// Print the minimum sum
System.out.println(min_sum);
}
// Driver Code
public static void main(String args[])
{
// Given Nodes and start node
V = 7;
int start = 0;
Graph g = new Graph(V);
// Given graph
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(0, 3);
g.addEdge(1, 6);
g.addEdge(2, 4);
g.addEdge(3, 5);
// Function call
minSum_depth( start, V);
}
}
// This code is contributed by Stream_Cipher
Python3
# Python program for the above approach class Graph: def __init__(self, v): self.max_depth = 0 self.V = v self.adj = [] for i in range(v): self.adj.append([]) def addEdge(self, v, w): self.adj[v].append(w) def find_depth(self, visited, start, depth): # Mark the node start as true visited[start] = True # Update the maximum depth self.max_depth = max(self.max_depth, depth) # Recurr for the child node of # start node for n in self.adj[start]: if (not visited[n]): self.find_depth(visited, n, depth + 1) # Function to calculate min value # at every depth def dfs(self, start, visited, store_min_elements, depth): # Marking already visited # vertices as true visited[start] = True # Store the min value for # every depth store_min_elements[depth] = min( store_min_elements[depth], start) # Traverse Child node of start node for n in self.adj[start]: if (not visited[n]): self.dfs(n, visited, store_min_elements, depth + 1) # Function to calculate the sum def minSum_depth(self, start, total_nodes): visited = [False]*total_nodes # Calling function to know # the depth of graph self.find_depth(visited, start, 0) # Set all value of visited # to false again visited = [False]*total_nodes # Declaring list of # "max_depth + 1" size to # store min values at every # depth initialise list # with max number store_min_elements = [10000000] * (self.max_depth + 1) # Calling dfs function for # calculation of min element # at every depth self.dfs(start, visited, store_min_elements, 0) # Variable to store sum of # all min elements min_sum = 0 # Calculation of minimum sum for i in range(len(store_min_elements)): min_sum += store_min_elements[i] # Print the minimum sum print(min_sum) # Driver Code # Given Nodes and start node V = 7 start = 0 g = Graph(V) # Given graph g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(0, 3) g.addEdge(1, 6) g.addEdge(2, 4) g.addEdge(3, 5) # Function call g.minSum_depth(start, V) # This code is contributed by Lovely Jain
C#
// C# program for the above approach
using System;
using System.Collections.Generic;
class Graph{
private static int V;
private static int start;
// Variable to store depth of graph
public static int max_depth = 0;
private static List<int>[] adj;
Graph(int v)
{
V = v;
adj = new List<int>[v];
for(int i = 0; i < v; ++i)
adj[i] = new List<int>();
}
// Function to add an edge in a graph
void addEdge(int v, int w)
{
adj[v].Add(w);
}
// Function to know the depth of graph
void find_depth(bool []visited,
int start, int depth)
{
// Mark the node start as true
visited[start] = true;
// Update the maximum depth
max_depth = Math.Max(max_depth, depth);
// Recurr for the child node of
// start node
List<int> vList = adj[start];
foreach(var n in vList)
{
if (!visited[n])
find_depth(visited, n,
depth + 1);
}
}
// Function to calculate min value
// at every depth
void dfs(int start, bool []visited,
int []store_min_elements,
int depth)
{
// Marking already visited
// vertices as true
visited[start] = true;
// Store the min value for
// every depth
store_min_elements[depth] = Math.Min(
store_min_elements[depth], start);
// Traverse Child node of start node
List<int> vList = adj[start];
foreach(var n in vList)
{
if (!visited[n])
dfs(n, visited,
store_min_elements,
depth + 1);
}
}
// Function to calculate the sum
void minSum_depth(int start, int total_nodes)
{
bool []visited = new bool[total_nodes];
// Calling function to know
// the depth of graph
find_depth(visited, start, 0);
// Set all value of visited
// to false again
for(int i = 0; i < visited.Length; i++)
{
visited[i] = false;
}
// Declaring vector of "max_depth + 1"
// size to store min values at every
// depth initialise vector with max number
int []store_min_elements = new int [max_depth + 1];
for(int i = 0;
i < store_min_elements.Length;
i++)
{
store_min_elements[i] = Int32.MaxValue;
}
// Calling dfs function for
// calculation of min element
// at every depth
dfs(start, visited, store_min_elements, 0);
// Variable to store sum of
// all min elements
int min_sum = 0;
// Calculation of minimum sum
for(int i = 0;
i < store_min_elements.Length;
i++)
{
min_sum += store_min_elements[i];
}
// Print the minimum sum
Console.WriteLine(min_sum);
}
// Driver Code
public static void Main()
{
// Given Nodes and start node
V = 7;
start = 0;
Graph g = new Graph(V);
// Given graph
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(0, 3);
g.addEdge(1, 6);
g.addEdge(2, 4);
g.addEdge(3, 5);
// Function call
g.minSum_depth(start , V);
}
}
// This code is contributed by Stream_Cipher
Javascript
<script>
// JavaScript program for the above approach
var V = 0;
var start = 0;
// Variable to store depth of graph
var max_depth = 0;
var adj;
function initialize( v)
{
V = v;
adj = Array.from(Array(v), ()=>Array());
}
// Function to add an edge in a graph
function addEdge(v, w)
{
adj[v].push(w);
}
// Function to know the depth of graph
function find_depth(visited, start, depth)
{
// Mark the node start as true
visited[start] = true;
// Update the maximum depth
max_depth = Math.max(max_depth, depth);
// Recurr for the child node of
// start node
var vList = adj[start];
for(var n of vList)
{
if (!visited[n])
find_depth(visited, n,
depth + 1);
}
}
// Function to calculate min value
// at every depth
function dfs(start, visited, store_min_elements, depth)
{
// Marking already visited
// vertices as true
visited[start] = true;
// Store the min value for
// every depth
store_min_elements[depth] = Math.min(
store_min_elements[depth], start);
// Traverse Child node of start node
var vList = adj[start];
for(var n of vList)
{
if (!visited[n])
dfs(n, visited,
store_min_elements,
depth + 1);
}
}
// Function to calculate the sum
function minSum_depth(start, total_nodes)
{
var visited = Array(total_nodes).fill(false);
// Calling function to know
// the depth of graph
find_depth(visited, start, 0);
// Set all value of visited
// to false again
for(var i = 0; i < visited.length; i++)
{
visited[i] = false;
}
// Declaring vector of "max_depth + 1"
// size to store min values at every
// depth initialise vector with max number
var store_min_elements = Array(max_depth+1).fill(0);
for(var i = 0;
i < store_min_elements.length;
i++)
{
store_min_elements[i] = 1000000000;
}
// Calling dfs function for
// calculation of min element
// at every depth
dfs(start, visited, store_min_elements, 0);
// Variable to store sum of
// all min elements
var min_sum = 0;
// Calculation of minimum sum
for(var i = 0;
i < store_min_elements.length;
i++)
{
min_sum += store_min_elements[i];
}
// Print the minimum sum
document.write(min_sum);
}
// Driver Code
// Given Nodes and start node
V = 7;
start = 0;
initialize(V);
// Given graph
addEdge(0, 1);
addEdge(0, 2);
addEdge(0, 3);
addEdge(1, 6);
addEdge(2, 4);
addEdge(3, 5);
// Function call
minSum_depth(start , V);
</script>
5
Complejidad Temporal: O(V + E)
Espacio Auxiliar: O(V)