Suma máxima de padres e hijos en el árbol binario

Dado un árbol binario, encuentre la suma máxima en un árbol binario agregando el padre con sus hijos. Se deben agregar exactamente tres Nodes. Si el árbol no tiene un Node con sus dos hijos como no NULL, devuelve 0.
 

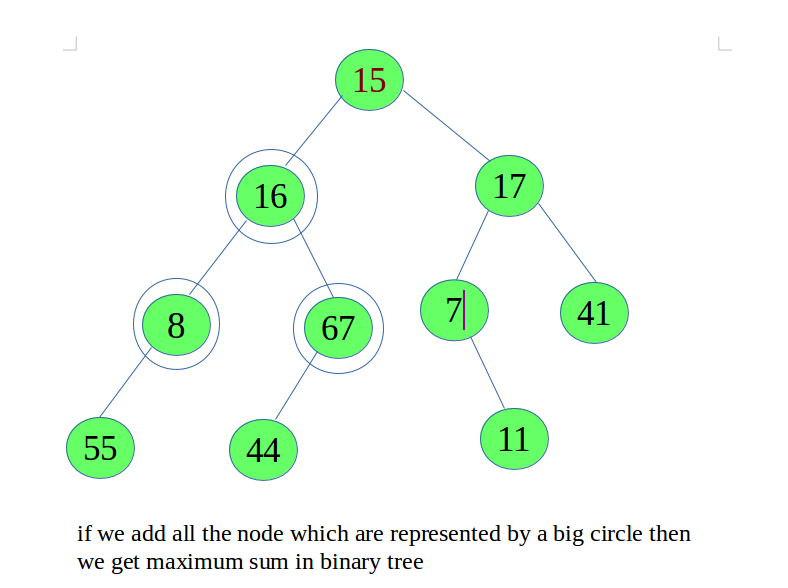
Simplemente recorremos el árbol y encontramos el Node que tiene la suma máxima. Tenemos que cuidar las hojas. 

// C++ program to find maximum sum of a node
// and its children
#include <iostream>
using namespace std;
 
struct Node {
    int data;
    struct Node *left, *right;
};
 
 
// insertion of Node in Tree
struct Node* newNode(int n)
{
    struct Node* root = new Node();
    root->data = n;
    root->left = root->right = NULL;
    return root;
}
 
int maxSum(struct Node* root)
{
    if (root == NULL)
        return 0;
 
    int res = maxSum(root->left);
 
    // if left and right link are null then
    // add all the three Node
    if (root->left != NULL && root->right != NULL) {
        int sum = root->data + root->left->data + root->right->data;
        res = max(res, sum);
    }
 
    return max(res, maxSum(root->right));
}
 
int main()
{
    struct Node* root =  newNode(15);
    root->left = newNode(16);
    root->left->left = newNode(8);
    root->left->left->left = newNode(55);
    root->left->right = newNode(67);
    root->left->right->left = newNode(44);
    root->right = newNode(17);
    root->right->left = newNode(7);
    root->right->left->right = newNode(11);
    root->right->right = newNode(41);
    cout << maxSum(root);
    return 0;
}

// Java program to find
// maximum sum of a node
// and its children
import java.util.*;
 
// insertion of Node in Tree
class Node
{
    int data;
    Node left, right;
     
     
    Node(int key)
    {
        data = key;
        left = right = null;
    }
}
class GFG
{
    public static int maxSum(Node root)
    {
        if (root == null)
        return 0;
 
    int res = maxSum(root.left);
 
    // if left and right link are null
    // then add all the three Node
    if (root.left != null &&
        root.right != null)
    {
        int sum = root.data +
                  root.left.data +
                  root.right.data;
        res = Math.max(res, sum);
    }
 
    return Math.max(res, maxSum(root.right));
    }
     
    // Driver code
    public static void main (String[] args)
    {
        Node root = new Node(15);
        root.left = new Node(16);
        root.left.right = new Node(67);
        root.left.right.left = new Node(44);
        root.left.left = new Node(8);
        root.left.left.left = new Node(55);
        root.right = new Node(17);
        root.right.right = new Node(41);
        root.right.left = new Node(7);
        root.right.left.right = new Node(11);
        System.out.print(maxSum(root));
    }
}
 
// This code is contributed
// by akash1295

# Python program to find maximum
# sum of a node and its children
class newNode():
 
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
 
def maxSum(root):
 
    if (root == None):
        return 0
 
    res = maxSum(root.left)
 
    # if left and right link are None then
    # add all the three Node
    if (root.left != None and root.right != None):
        sum = root.data + root.left.data + root.right.data
        res = max(res, sum)
 
    return max(res, maxSum(root.right))
     
# Driver code
if __name__ == '__main__':
    root = newNode(15)
    root.left = newNode(16)
    root.left.left = newNode(8)
    root.left.left.left = newNode(55)
    root.left.right = newNode(67)
    root.left.right.left = newNode(44)
    root.right = newNode(17)
    root.right.left = newNode(7)
    root.right.left.right = newNode(11)
    root.right.right = newNode(41)
    print(maxSum(root))
 
# This code is contributed by SHUBHAMSINGH10

// C# program to find
// maximum sum of a node
// and its children
using System;
 
// insertion of Node in Tree
public class Node
{
    public int data;
    public Node left, right;
      
      
    public Node(int key)
    {
        data = key;
        left = right = null;
    }
}
public class GFG
{
    public static int maxSum(Node root)
    {
        if (root == null)
        return 0;
  
    int res = maxSum(root.left);
  
    // if left and right link are null
    // then add all the three Node
    if (root.left != null &&
        root.right != null)
    {
        int sum = root.data +
                  root.left.data +
                  root.right.data;
        res = Math.Max(res, sum);
    }
  
    return Math.Max(res, maxSum(root.right));
    }
      
    // Driver code
    public static void Main ()
    {
        Node root = new Node(15);
        root.left = new Node(16);
        root.left.right = new Node(67);
        root.left.right.left = new Node(44);
        root.left.left = new Node(8);
        root.left.left.left = new Node(55);
        root.right = new Node(17);
        root.right.right = new Node(41);
        root.right.left = new Node(7);
        root.right.left.right = new Node(11);
        Console.Write(maxSum(root));
    }
}
 
/* This code is contributed PrinciRaj1992 */

<script>
 
// Javascript program to find
// maximum sum of a node
// and its children
 
// Insertion of Node in Tree
class Node
{
    constructor(key)
    {
        this.data = key;
        this.left = null;
        this.right = null;
    }
}
 
function maxSum(root)
{
    if (root == null)
        return 0;
 
    var res = maxSum(root.left);
     
    // If left and right link are null
    // then add all the three Node
    if (root.left != null &&
        root.right != null)
    {
        var sum = root.data +
                  root.left.data +
                  root.right.data;
        res = Math.max(res, sum);
    }
     
    return Math.max(res, maxSum(root.right));
}
  
// Driver code
var root = new Node(15);
root.left = new Node(16);
root.left.right = new Node(67);
root.left.right.left = new Node(44);
root.left.left = new Node(8);
root.left.left.left = new Node(55);
root.right = new Node(17);
root.right.right = new Node(41);
root.right.left = new Node(7);
root.right.left.right = new Node(11);
document.write(maxSum(root));
 
// This code is contributed by rutvik_56
 
</script>

Producción: 

91