La técnica de descomposición Sqrt (o raíz cuadrada) es una de las técnicas de optimización de consultas más comunes que utilizan los programadores de la competencia . Esta técnica nos ayuda a reducir la complejidad del tiempo en un factor de sqrt(n) .
El concepto clave de esta técnica es descomponer una array dada en pequeños fragmentos específicamente de tamaño sqrt(n).
Digamos que tenemos una array de n elementos y la descomponemos en pequeños fragmentos de tamaño sqrt(n). Tendremos exactamente sqrt(n) tales trozos siempre que n sea un cuadrado perfecto. Por lo tanto, ahora nuestra array en n elementos se descompone en bloques sqrt (n), donde cada bloque contiene elementos sqrt (n) (suponiendo que el tamaño de la array es un cuadrado perfecto).
Consideremos estos fragmentos o bloques como una array individual, cada uno de los cuales contiene elementos sqrt (n) y ha calculado la respuesta deseada (de acuerdo con su problema) individualmente para todos los fragmentos. Ahora, debe responder ciertas consultas que le piden la respuesta de los elementos en el rango l a r (l y r son índices iniciales y finales de la array) en la array original de tamaño n.
El enfoque ingenuo es simplemente iterar sobre cada elemento en el rango de l a r y calcular su respuesta correspondiente. Por lo tanto, la Complejidad de Tiempo por consulta será O(n).
Truco de descomposición Sqrt:Como ya hemos calculado previamente la respuesta para todos los fragmentos individuales y ahora necesitamos responder las consultas en el rango l a r. Ahora podemos simplemente combinar las respuestas de los fragmentos que se encuentran entre el rango de l a r en la array original. Entonces, si observamos cuidadosamente aquí, estamos saltando sqrt (n) pasos a la vez en lugar de saltar 1 paso a la vez como se hace en un enfoque ingenuo. Analicemos su Complejidad de tiempo e implementación considerando el siguiente problema: –
Problem : Given an array of n elements. We need to answer q queries telling the sum of elements in range l to r in the array. Also the array is not static i.e the values are changed via some point update query. Range Sum Queries are of form : Q l r , where l is the starting index r is the ending index Point update Query is of form : U idx val, where idx is the index to update val is the updated value
Consideremos que tenemos un arreglo de 9 elementos.
A[] = {1, 5, 2, 4, 6, 1, 3, 5, 7}
Descompongamos esta array en bloques sqrt(9), donde cada bloque contendrá la suma de los elementos que se encuentran en él. Por lo tanto, ahora nuestra array descompuesta se vería así:
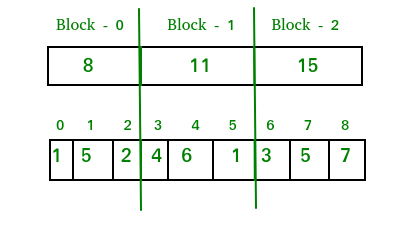
Hasta ahora hemos construido la array descompuesta de bloques sqrt(9) y ahora necesitamos imprimir la suma de elementos en un rango dado. Entonces, primero veamos dos tipos básicos de superposición que una consulta de rango puede tener en nuestra array:
Consulta de rango de tipo 1 (el rango dado está en los límites del bloque):

En este tipo de consulta, el rango puede cubrir totalmente los bloques sqrt continuos. Entonces podemos responder fácilmente a la suma de valores en este rango como la suma de bloques completamente superpuestos.
Entonces, la respuesta a la consulta anterior en la imagen descrita será: ans = 11 + 15 = 26
Complejidad de tiempo: en el peor de los casos, nuestro rango puede ser de 0 a n-1 (donde n es el tamaño de la array y suponiendo que n sea un perfecto cuadrado). En este caso, todos los bloques están completamente superpuestos por nuestro rango de consulta. Por lo tanto, para responder a esta consulta necesitamos iterar sobre todos los bloques descompuestos de la array y sabemos que el número de bloques = sqrt(n). Por lo tanto, la complejidad para este tipo de consulta será O(sqrt(n)) en el peor de los casos.
Consulta de rango de tipo 2 (el rango dado NO está en los límites)
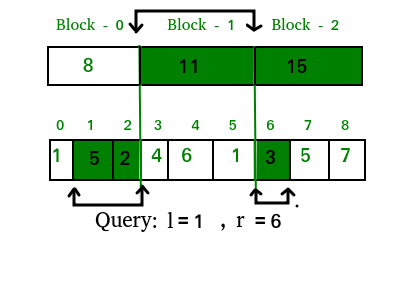
Podemos tratar este tipo de consultas sumando los datos de los bloques descompuestos completamente superpuestos que se encuentran en el rango de consulta y luego sumando los elementos uno por uno de la array original cuyo bloque correspondiente no está completamente superpuesto por el rango de consulta.
Entonces, la respuesta a la consulta anterior en la imagen descrita será: ans = 5 + 2 + 11 + 3 = 21
Complejidad de tiempo:Consideremos una consulta [l = 1 y r = n-2] (n es el tamaño de la array y tiene una indexación basada en 0). Por lo tanto, para esta consulta exactamente ( sqrt(n) – 2 ) los bloques se superpondrán por completo, mientras que el primer y el último bloque se superpondrán parcialmente y solo quedará un elemento fuera del rango de superposición. Por lo tanto, los bloques completamente superpuestos se pueden resumir en ( sqrt(n) – 2 ) ~ sqrt(n) iteraciones, mientras que el primer y el último bloque deben atravesarse uno por uno por separado. Pero como sabemos que la cantidad de elementos en cada bloque está en max sqrt (n), para resumir el último bloque individualmente, debemos hacer,
(sqrt (n) -1) ~ sqrt (n) iteraciones y lo mismo para el último bloquear.
Entonces, la Complejidad total = O(sqrt(n)) + O(sqrt(n)) + O(sqrt(n)) = O(3*sqrt(N)) = O(sqrt(n))
Consultas de actualización (actualización de puntos):
En esta consulta, simplemente encontramos el bloque en el que se encuentra el índice dado, luego restamos su valor anterior y agregamos el nuevo valor actualizado según la consulta de actualización de puntos.
Complejidad de tiempo : O(1)
Implementación:
La implementación del truco anterior se da a continuación.
C++
// C++ program to demonstrate working of Square Root
// Decomposition.
#include "iostream"
#include "math.h"
using namespace std;
#define MAXN 10000
#define SQRSIZE 100
int arr[MAXN]; // original array
int block[SQRSIZE]; // decomposed array
int blk_sz; // block size
// Time Complexity : O(1)
void update(int idx, int val)
{
int blockNumber = idx / blk_sz;
block[blockNumber] += val - arr[idx];
arr[idx] = val;
}
// Time Complexity : O(sqrt(n))
int query(int l, int r)
{
int sum = 0;
while (l<r and l%blk_sz!=0 and l!=0)
{
// traversing first block in range
sum += arr[l];
l++;
}
while (l+blk_sz-1 <= r)
{
// traversing completely overlapped blocks in range
sum += block[l/blk_sz];
l += blk_sz;
}
while (l<=r)
{
// traversing last block in range
sum += arr[l];
l++;
}
return sum;
}
// Fills values in input[]
void preprocess(int input[], int n)
{
// initiating block pointer
int blk_idx = -1;
// calculating size of block
blk_sz = sqrt(n);
// building the decomposed array
for (int i=0; i<n; i++)
{
arr[i] = input[i];
if (i%blk_sz == 0)
{
// entering next block
// incrementing block pointer
blk_idx++;
}
block[blk_idx] += arr[i];
}
}
// Driver code
int main()
{
// We have used separate array for input because
// the purpose of this code is to explain SQRT
// decomposition in competitive programming where
// we have multiple inputs.
int input[] = {1, 5, 2, 4, 6, 1, 3, 5, 7, 10};
int n = sizeof(input)/sizeof(input[0]);
preprocess(input, n);
cout << "query(3,8) : " << query(3, 8) << endl;
cout << "query(1,6) : " << query(1, 6) << endl;
update(8, 0);
cout << "query(8,8) : " << query(8, 8) << endl;
return 0;
}
Java
// Java program to demonstrate working of
// Square Root Decomposition.
import java.util.*;
class GFG
{
static int MAXN = 10000;
static int SQRSIZE = 100;
static int []arr = new int[MAXN]; // original array
static int []block = new int[SQRSIZE]; // decomposed array
static int blk_sz; // block size
// Time Complexity : O(1)
static void update(int idx, int val)
{
int blockNumber = idx / blk_sz;
block[blockNumber] += val - arr[idx];
arr[idx] = val;
}
// Time Complexity : O(sqrt(n))
static int query(int l, int r)
{
int sum = 0;
while (l < r && l % blk_sz != 0 && l != 0)
{
// traversing first block in range
sum += arr[l];
l++;
}
while (l+blk_sz-1 <= r)
{
// traversing completely
// overlapped blocks in range
sum += block[l / blk_sz];
l += blk_sz;
}
while (l <= r)
{
// traversing last block in range
sum += arr[l];
l++;
}
return sum;
}
// Fills values in input[]
static void preprocess(int input[], int n)
{
// initiating block pointer
int blk_idx = -1;
// calculating size of block
blk_sz = (int) Math.sqrt(n);
// building the decomposed array
for (int i = 0; i < n; i++)
{
arr[i] = input[i];
if (i % blk_sz == 0)
{
// entering next block
// incrementing block pointer
blk_idx++;
}
block[blk_idx] += arr[i];
}
}
// Driver code
public static void main(String[] args)
{
// We have used separate array for input because
// the purpose of this code is to explain SQRT
// decomposition in competitive programming where
// we have multiple inputs.
int input[] = {1, 5, 2, 4, 6, 1, 3, 5, 7, 10};
int n = input.length;
preprocess(input, n);
System.out.println("query(3, 8) : " +
query(3, 8));
System.out.println("query(1, 6) : " +
query(1, 6));
update(8, 0);
System.out.println("query(8, 8) : " +
query(8, 8));
}
}
// This code is contributed by PrinciRaj1992
Python 3
# Python 3 program to demonstrate working of Square Root
# Decomposition.
from math import sqrt
MAXN = 10000
SQRSIZE = 100
arr = [0]*(MAXN) # original array
block = [0]*(SQRSIZE) # decomposed array
blk_sz = 0 # block size
# Time Complexity : O(1)
def update(idx, val):
blockNumber = idx // blk_sz
block[blockNumber] += val - arr[idx]
arr[idx] = val
# Time Complexity : O(sqrt(n))
def query(l, r):
sum = 0
while (l < r and l % blk_sz != 0 and l != 0):
# traversing first block in range
sum += arr[l]
l += 1
while (l + blk_sz - 1 <= r):
# traversing completely overlapped blocks in range
sum += block[l//blk_sz]
l += blk_sz
while (l <= r):
# traversing last block in range
sum += arr[l]
l += 1
return sum
# Fills values in input[]
def preprocess(input, n):
# initiating block pointer
blk_idx = -1
# calculating size of block
global blk_sz
blk_sz = int(sqrt(n))
# building the decomposed array
for i in range(n):
arr[i] = input[i];
if (i % blk_sz == 0):
# entering next block
# incrementing block pointer
blk_idx += 1;
block[blk_idx] += arr[i]
# Driver code
# We have used separate array for input because
# the purpose of this code is to explain SQRT
# decomposition in competitive programming where
# we have multiple inputs.
input= [1, 5, 2, 4, 6, 1, 3, 5, 7, 10]
n = len(input)
preprocess(input, n)
print("query(3,8) : ",query(3, 8))
print("query(1,6) : ",query(1, 6))
update(8, 0)
print("query(8,8) : ",query(8, 8))
# This code is contributed by Sanjit_Prasad
C#
// C# program to demonstrate working of
// Square Root Decomposition.
using System;
class GFG
{
static int MAXN = 10000;
static int SQRSIZE = 100;
static int []arr = new int[MAXN]; // original array
static int []block = new int[SQRSIZE]; // decomposed array
static int blk_sz; // block size
// Time Complexity : O(1)
static void update(int idx, int val)
{
int blockNumber = idx / blk_sz;
block[blockNumber] += val - arr[idx];
arr[idx] = val;
}
// Time Complexity : O(sqrt(n))
static int query(int l, int r)
{
int sum = 0;
while (l < r && l % blk_sz != 0 && l != 0)
{
// traversing first block in range
sum += arr[l];
l++;
}
while (l + blk_sz - 1 <= r)
{
// traversing completely
// overlapped blocks in range
sum += block[l / blk_sz];
l += blk_sz;
}
while (l <= r)
{
// traversing last block in range
sum += arr[l];
l++;
}
return sum;
}
// Fills values in input[]
static void preprocess(int []input, int n)
{
// initiating block pointer
int blk_idx = -1;
// calculating size of block
blk_sz = (int) Math.Sqrt(n);
// building the decomposed array
for (int i = 0; i < n; i++)
{
arr[i] = input[i];
if (i % blk_sz == 0)
{
// entering next block
// incrementing block pointer
blk_idx++;
}
block[blk_idx] += arr[i];
}
}
// Driver code
public static void Main(String[] args)
{
// We have used separate array for input because
// the purpose of this code is to explain SQRT
// decomposition in competitive programming where
// we have multiple inputs.
int []input = {1, 5, 2, 4, 6, 1, 3, 5, 7, 10};
int n = input.Length;
preprocess(input, n);
Console.WriteLine("query(3, 8) : " +
query(3, 8));
Console.WriteLine("query(1, 6) : " +
query(1, 6));
update(8, 0);
Console.WriteLine("query(8, 8) : " +
query(8, 8));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to demonstrate working of
// Square Root Decomposition.
let MAXN = 10000;
let SQRSIZE = 100;
let arr = new Array(MAXN);
for(let i = 0; i < MAXN; i++)
{
arr[i] = 0;
}
let block = new Array(SQRSIZE);
for(let i = 0; i < SQRSIZE; i++)
{
block[i] = 0;
}
let blk_sz;
// Time Complexity : O(1)
function update(idx,val)
{
let blockNumber = idx / blk_sz;
block[blockNumber] += val - arr[idx];
arr[idx] = val;
}
// Time Complexity : O(sqrt(n))
function query(l, r)
{
let sum = 0;
while (l < r && l % blk_sz != 0 && l != 0)
{
// traversing first block in range
sum += arr[l];
l++;
}
while (l+blk_sz-1 <= r)
{
// traversing completely
// overlapped blocks in range
sum += block[l / blk_sz];
l += blk_sz;
}
while (l <= r)
{
// traversing last block in range
sum += arr[l];
l++;
}
return sum;
}
// Fills values in input[]
function preprocess(input, n)
{
// initiating block pointer
let blk_idx = -1;
// calculating size of block
blk_sz = Math.floor( Math.sqrt(n));
// building the decomposed array
for (let i = 0; i < n; i++)
{
arr[i] = input[i];
if (i % blk_sz == 0)
{
// entering next block
// incrementing block pointer
blk_idx++;
}
block[blk_idx] += arr[i];
}
}
// Driver code
// We have used separate array for input because
// the purpose of this code is to explain SQRT
// decomposition in competitive programming where
// we have multiple inputs.
let input = [1, 5, 2, 4, 6, 1, 3, 5, 7, 10];
let n = input.length;
preprocess(input, n);
document.write("query(3, 8) : " +
query(3, 8)+"<br>");
document.write("query(1, 6) : " +
query(1, 6)+"<br>");
update(8, 0);
document.write("query(8, 8) : " +
query(8, 8)+"<br>");
// This code is contributed by rag2127
</script>
query(3,8) : 26 query(1,6) : 21 query(8,8) : 0
Complejidad de tiempo: O(n)
Espacio auxiliar : O (MAXN)
Nota: el código anterior funciona incluso si n no es un cuadrado perfecto. En el caso, el último bloque contendrá aún menos cantidad de elementos que sqrt(n), reduciendo así la cantidad de iteraciones.
Digamos n = 10. En este caso, tendremos 4 bloques, los primeros tres bloques de tamaño 3 y el último bloque de tamaño 1.
Este artículo es una contribución de Nitish Kumar . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA