Teorema de Arden en Teoría de la Computación

El teorema de Arden establece que:
«Si P y Q son dos expresiones regulares sobre , y si P no contiene , entonces la siguiente ecuación en R dada por R = Q + RP tiene una solución única, es decir, R = QP*».
Eso significa que, siempre que obtengamos una ecuación en la forma de R = Q + RP, podemos reemplazarla directamente por R = QP*. Entonces, aquí primero probaremos que R = QP* es la solución de esta ecuación y luego también probaremos que es la única solución de esta ecuación.

Comencemos tomando esta ecuación como ecuación (i)

R = Q + RP  ......(i)

Ahora, reemplazando R por R = QP*, obtenemos,

R = Q + QP*P 

Tomando Q como común,

R = Q( + P*P)
R = QP*  

(Como sabemos que + R*R = R*). Por lo tanto probado.

Así, R = QP* es la solución de la ecuación R = Q + RP.

Ahora, tenemos que demostrar que esta es la única solución de esta ecuación. Déjame tomar esta ecuación de nuevo:

R = Q + RP

Ahora, reemplaza R por R = Q + RP,

R = Q + (Q + RP)P
  = Q + QP + R 

Nuevamente, reemplace R por R = Q + RP: –

R = Q + QP + (Q + RP) 
  = Q + QP + Q + R
  = ...
  = ...
  =  Q + QP + Q + .. + Q + R 

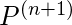
Ahora, reemplazando R por R = QP*, obtenemos,

R = Q + QP + Q + .. + Q + QP* 

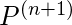
Tomando Q como común,

R = Q( + P +  + .. +  + P*)
  = QP*    [As  + P +  + .. +  + P* represent 
          the closure of P] 

Por lo tanto probado.

Así, R = QP* es la única solución de la ecuación R = Q + RP.

Para entender este teorema, resolveremos un ejemplo:

Ejemplo –

q1 = q1.0  + 
q2 = q1.1 + q2.0
q3 = q2.1 + q3.0 + q3.1 

Ahora,

q1 =  + q1.0
q1 = .0*    [By Arden's theorem]
q1 = 0*      [R = R]

.'. q2 = 0*1 +q2.0
    q2 = 0*10*    

[Aplicando el teorema de Arden]. Por lo tanto, el valor de q2 es 0*10*.