Recomendamos encarecidamente consultar la publicación a continuación como requisito previo para esto.
Fórmula de Bayes
A continuación se muestra la fórmula de Bayes.![]()
La fórmula proporciona la relación entre P(A|B) y P(B|A). Se deriva principalmente de la fórmula de probabilidad condicional discutida en la publicación anterior .
Considere las siguientes fórmulas para las probabilidades condicionales P(A|B) y P(B|A) ![]() —-(1)
—-(1)
![]() —-(2)
—-(2)
Como P(B ∩ A) = P(A ∩ B), podemos reemplazar P(A ∩ B) en la primera fórmula con P(B|A)P(A)
Después de reemplazar, obtenemos la fórmula dada.
Regla del producto
La regla del producto establece que
![]()
Entonces, la probabilidad conjunta de que ocurran tanto X como Y es igual al producto de dos términos:
De la regla del producto: ![]() implica P(X|Y) = P(X)/P(Y)
implica P(X|Y) = P(X)/P(Y)![]() implica P(X|Y) = 1
implica P(X|Y) = 1
String de reglas
Cuando la regla del producto anterior se generaliza, llevamos a la regla de la string. Sean ![]() n eventos. Entonces, la probabilidad conjunta viene dada por
n eventos. Entonces, la probabilidad conjunta viene dada por
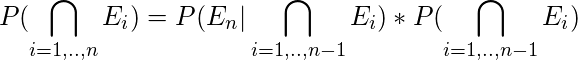
Teorema de Bayes
De la regla del producto, ![]() y
y ![]() . Como
. Como ![]() y
y ![]() son iguales.
son iguales.
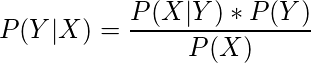
donde ![]() _
_
Ejemplo: la caja P tiene 2 bolas rojas y 3 bolas azules y la caja Q tiene 3 bolas rojas y 1 bola azul. Una pelota se selecciona de la siguiente manera:
(i) Select a box
(ii) Choose a ball from the selected box such that each ball in
the box is equally likely to be chosen. The probabilities of
selecting boxes P and Q are (1/3) and (2/3), respectively.
Dado que una bola seleccionada en el proceso anterior es una bola roja, la probabilidad de que provenga de la caja P es (GATE CS 2005)
(A) 4/19
(B) 5/19
(C) 2/9
(D) 19/30
Solución:
R --> Event that red ball is selected B --> Event that blue ball is selected P --> Event that box P is selected Q --> Event that box Q is selected We need to calculate P(P|R)?P(R|P) = A red ball selected from box P = 2/5 P(P) = 1/3 P(R) = P(P)*P(R|P) + P(Q)*P(R|Q) = (1/3)*(2/5) + (2/3)*(3/4) = 2/15 + 1/2 = 19/30 Putting above values in the Bayes's Formula P(P|R) = (2/5)*(1/3) / (19/30) = 4/19
Ejercicio Una empresa compra el 70% de sus computadoras a la empresa X y el 30% a la empresa Y. La empresa X produce 1 computadora defectuosa por cada 5 computadoras y la empresa Y produce 1 computadora defectuosa por cada 20 computadoras. Una computadora se encuentra defectuosa ¿cuál es la probabilidad de que haya sido comprada a la empresa X?
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA