Teorema de Kleene en TOC | Parte 1

Se dice que un lenguaje es regular si se puede representar usando un autómata finito o si se puede generar una expresión regular para él. Esta definición nos lleva a la definición general que; Por cada Expresión Regular correspondiente al lenguaje, se puede generar un Autómata Finito.

Para ciertas expresiones como :- (a+b), ab, (a+b)* ; Es bastante más fácil hacer Finite Automata solo con la intuición, como se muestra a continuación. El problema surge cuando se nos proporciona una Expresión Regular más larga. Esto trae consigo la necesidad de un enfoque sistemático hacia la generación de FA, que ha sido presentado por Kleene en el Teorema de Kleene – I

Teorema de Kleene-I:

Para cualquier expresión regular r que represente el idioma L(r), existe un autómata finito que acepta el mismo idioma.

Para entender el Teorema-I de Kleene, tomemos en cuenta la definición básica de Expresión Regular donde observamos que , y un solo símbolo de entrada “a” se pueden incluir en un Lenguaje Regular y las operaciones correspondientes que se pueden realizar mediante la combinación de estos son:

Decir y ser dos expresiones regulares. Después,

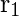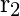1. + es también una expresión regular, cuyo lenguaje correspondiente es L( 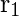) UL( )
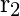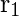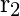2. . es también una expresión regular, cuyo lenguaje correspondiente es L( 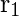).L( )
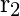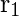3. * es también una expresión regular, cuyo lenguaje correspondiente es L( )*

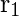Además, podemos usar esta definición en asociación con transiciones nulas para dar lugar a un FA mediante la combinación de dos o más autómatas finitos más pequeños (cada uno correspondiente a una expresión regular).

Si S acepta L = {a} y T acepta L = {b}, entonces R puede representarse como una combinación de S y T usando las operaciones proporcionadas como:

R = S + T

Observamos que,

1. En caso de operación de unión, podemos tener un nuevo estado de inicio, desde el cual, la transición nula procede al estado de inicio de ambas máquinas de estados finitos.
2. Los estados finales de ambos autómatas finitos se convierten en estados intermedios. El estado final se unifica en uno que puede ser atravesado por transiciones nulas.

R = S.T 

Observamos que,

1. En caso de operación de concatenación podemos tener el mismo estado inicial que el de S, el único cambio ocurre en el estado final de S, el cual se convierte a un estado intermedio seguido de una Transición Nula.
2. La transición nula es seguida por el estado inicial de T, el estado final de T se usa como el estado final de R.

 R = S*

Observamos que,

1. Se agrega un nuevo estado de inicio, y S se ha puesto como un estado intermedio para que se pueda incorporar la condición de bucle automático.
2. Los estados inicial y final se han definido por separado para que no se altere la condición de bucle automático.

Ahora que somos conscientes de las operaciones generales. Veamos cómo se puede usar el Teorema-I de Kleene para generar un FA para la expresión regular dada.

Example:
Make a Finite Automata for the expression (ab+a)* 

Vemos que usar el Teorema de Kleene – I da un enfoque sistemático hacia la generación de Autómatas Finitos para la Expresión Regular provista.