Teorema de la energía del trabajo

El concepto “obra” es de uso común en el habla ordinaria, y entendemos que se refiere al acto de realizar algo. Por ejemplo, ¡actualmente estás mejorando tu comprensión de la física al leer este artículo! Sin embargo, la Física puede estar en desacuerdo en este punto. ¡El teorema del trabajo y la energía explica por qué existe esta física del no trabajo!

Cuando una fuerza operativa desplaza una partícula, se dice que se ha realizado trabajo. No hay trabajo hecho si no hay reubicación. Puede fatigarse si permanece de pie durante un período prolongado de tiempo, pero según la física, no ha realizado ningún trabajo.

¿Qué es trabajo?

El trabajo realizado sobre un sistema por una fuerza constante es el producto de la componente de la fuerza en la dirección del movimiento por la distancia a través de la cual actúa la fuerza.

El trabajo realizado en un movimiento unidimensional se puede expresar en forma de ecuación como

W = Fdcosθ

donde W es trabajo, F es la magnitud de la fuerza del sistema, d la magnitud del desplazamiento del sistema y θ es el ángulo entre el vector de fuerza F y el vector de desplazamiento d.

El trabajo realizado puede ser positivo, negativo o incluso cero.

Trabajo positivo : cuando una fuerza mueve un objeto en su dirección, el trabajo realizado se considera positivo. Ejemplo: El movimiento de una pelota que cae hacia la tierra, donde se mide el desplazamiento de la pelota, es un ejemplo de este tipo de trabajo. La pelota se mueve en la dirección de la gravedad.
Trabajo negativo : cuando la fuerza y el desplazamiento tienen direcciones opuestas, se supone que el trabajo es negativo. Ejemplo: Cuando se lanza una pelota hacia arriba, por ejemplo, el desplazamiento será hacia arriba; sin embargo, la fuerza debida al rozamiento será hacia abajo. La gravedad de la tierra estará en una dirección hacia abajo.
Trabajo cero: el trabajo total realizado por la fuerza sobre el objeto es cero si la dirección de la fuerza y el desplazamiento son perpendiculares entre sí. Ejemplo: Cuando empujamos con fuerza contra una pared, por ejemplo, la fuerza que estamos ejerciendo sobre la pared es ineficaz ya que el desplazamiento de la pared es igual a d = 0.

¿Qué es energía?

La capacidad de trabajo se define como energía. Algunos tipos de energía incluyen energía potencial, energía cinética, energía térmica, energía eléctrica, energía química y energía nuclear. El movimiento está vinculado a todas las fuentes de energía. Cuando un cuerpo está en movimiento, por ejemplo, tiene energía cinética. Cuando un objeto tenso, como un arco o un resorte, está en reposo, tiene la capacidad de crear movimiento; su configuración contiene energía potencial. La energía nuclear también es energía potencial porque surge de la disposición de las partículas subatómicas en el núcleo de un átomo.

Hay muchas formas de energía como se mencionó anteriormente. Aquí nos enfocamos principalmente en la energía cinética.

Energía cinética:

La energía cinética es el tipo de energía que tiene un objeto o partícula como resultado de su movimiento.
Cuando se realiza trabajo sobre un objeto ejerciendo una fuerza neta, el objeto se acelera y, como resultado, gana energía cinética.
La energía cinética es una propiedad de un objeto o partícula en movimiento que está determinada tanto por su masa como por su movimiento.
Si el movimiento a lo largo de un camino de un lugar a otro, el tipo de energía cinética que posee el objeto es energía cinética de traslación, si la rotación alrededor de un eje, entonces el objeto posee energía cinética de rotación.

Energía cinética traslacional:
- La energía cinética de traslación de un cuerpo es igual a la mitad del producto de su masa, m, y su velocidad, v, o $\frac{1}{2}mv^2$
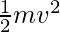
- Esta fórmula solo es válida para partículas que se mueven a velocidades bajas o moderadas; para partículas realmente de alta velocidad, produce valores que son demasiado pequeños. Cuando un objeto se acerca a la velocidad de la luz (3 × 10 ⁸ metros por segundo, o 186 000 millas por segundo), su masa aumenta, lo que requiere la aplicación de las reglas de la relatividad.
- El aumento de masa de una partícula sobre su masa en reposo multiplicado por el cuadrado de la velocidad de la luz es igual a la energía cinética relativista.

Un Cuerpo de Masa M y moviéndose con Velocidad V

Energía cinética rotacional: el momento de inercia I, para un cuerpo giratorio, se relaciona con la masa, mientras que la velocidad angular (omega) se relaciona con la velocidad lineal o de traslación. Como resultado, la energía cinética de rotación es igual a la mitad del producto del momento de inercia y el cuadrado de la velocidad angular o $\frac{1}{2}Iω^2$

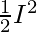
Un disco de masa M y radio r que gira a lo largo de su eje con velocidad angular ω

Teorema del trabajo y la energía

El enunciado del teorema de la energía del trabajo es,

El teorema del trabajo y la energía establece que el trabajo realizado por la suma de todas las fuerzas que actúan sobre una partícula es igual al cambio en la energía cinética de la partícula (o) El trabajo neto realizado en un sistema es igual al cambio en la energía cinética.

Teorema del trabajo y la energía

El trabajo W realizado por la fuerza neta sobre una partícula es igual al cambio en la energía cinética KE de la partícula.

$W=\triangle KE$

$W= \frac{1}{2}mv_f-\frac{1}{2}mv_i$

donde vi _y vf _son las velocidades de la partícula antes y después de la aplicación de la fuerza, y m es la masa de la partícula.

Derivación del trabajo realizado por fuerza constante

Consideremos el caso en el que la fuerza resultante F es constante tanto en magnitud como en dirección y es paralela a la velocidad de la partícula. La partícula se mueve con aceleración constante a, a lo largo de una línea recta.

Trabajo realizado por una fuerza constante

La relación entre la fuerza neta y la aceleración viene dada por la ecuación F = ma (segunda ley de Newton), y el desplazamiento d de la partícula se puede determinar a partir de la ecuación,

$v_f^2=v_i^2+2ad$ (de la ecuación $v^2=u^2+2as$ donde v=velocidad final, u=velocidad inicial y s=desplazamiento)

Obtenemos,

$d = \frac{v_f^2-v_i^2}{2a}$

El trabajo de la fuerza neta se calcula como el producto de su magnitud y el desplazamiento de la partícula (W=Fd).

Sustituyendo las ecuaciones anteriores se obtiene:

$W=F(\frac{v_f^2-v_i^2}{2a})$

$W=(ma)(\frac{v_f^2-v_i^2}{2a})$

$W=m(\frac{v_f^2-v_i^2}{2})$

$W=\frac{mv_f^2}{2}-\frac{mv_i^2}{2}$

W= $KE_f-KE_i$

$\triangle KE$

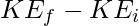
Por lo tanto, el trabajo neto realizado = cambio en energía cinética

Derivación del trabajo realizado por fuerza variable

Las fuerzas variables son las fuerzas más comunes que encontramos a diario. La fórmula trabajo-energía para la fuerza variable es un poco complicada de entender. Considere un gráfico con desplazamiento en un eje y fuerza variable en el otro. El eje x representa el desplazamiento, mientras que el eje y representa una fuerza en este gráfico. A lo largo del eje x, divida el área del gráfico en rectángulos de ancho arbitrariamente pequeños.

Trabajo realizado por una fuerza variable

Podemos suponer que la fuerza aplicada es constante para un desplazamiento $\triangle$ x arbitrariamente pequeño. Como resultado, tenemos;

⇒ $\triangle W=F(x) \triangle x$

Como integral definida de la fuerza sobre el desplazamiento neto, ahora podemos definir el trabajo como:

⇒ $W=\int_{x_i}^{x_f} F(x)dx$

Como la energía cinética es igual a $K=\frac{1}{2}mv^2$ ,

El cambio en la energía cinética con el tiempo se puede describir de la siguiente manera:

⇒ $\frac{d}{dt}(K)=\frac{d}{dt}(\frac{1}{2}mv^2)$

⇒ $\frac{dK}{dt}=m\frac{dv}{dt}$

La aceleración, según la segunda ley del movimiento de Newton, es el cambio de velocidad de un objeto con respecto al tiempo. Como resultado, la ecuación anterior se puede reescribir como,

⇒ $\frac{dK}{dt}=mav$

Podemos expresar la ecuación anterior como, porque F= ma y la velocidad es la tasa de cambio del desplazamiento en el tiempo.

⇒ $\frac{dK}{dt}=F \frac{dx}{dt}$

Cuando se eliminan ambos lados de las derivadas temporales de la ecuación, obtenemos

⇒ dK=Fdx

Al integrar la ecuación anterior a lo largo del eje x, obtenemos,

⇒ $\int_{x_i}^{x_f}dK=\int_{x_i}^{x_f}Fxdx$

⇒ $K_f-K_i=\int_{x_i}^{x_f}Fxdx$

o podemos escribir, $\triangle K=\int_{x_i}^{x_f}Fxdx$

Por lo tanto obtenemos, $\triangle K=W$

La ecuación anterior es la prueba del teorema del trabajo y la energía para la fuerza variable.

Problema de muestra

Problema 1: Se deja caer una pelota de 2 kg desde una altura de 10 m. Calcular el trabajo realizado sobre la pelota entre el momento en que se suelta y el momento en que toca el suelo. Suponga que se puede despreciar la resistencia del aire.

Solución:

Dado,

Masa de la pelota, m=2 kg.

Altura inicial de la pelota, h _i =10 m.

Altura final de la pelota, h _f =0 m.

Debemos calcular la cantidad de trabajo realizado sobre la pelota cuando golpea el suelo.

La pelota cae libremente aquí, conservando energía. Sabemos que la diferencia de energía cinética es igual al trabajo realizado.

Debido a que la pelota está inmóvil cuando se deja caer, al principio no tiene energía cinética.

Toda la energía potencial de la pelota se transforma en energía cinética cuando la pelota toca el suelo.

Entonces, la energía potencial de la pelota a la altura h _i es,

E _p = mgh

$E_p=2\times 9.8 \times 10=196 J$

Ahora, la pelota tenía 196 J de energía potencial cuando se soltó y 0 J de energía cinética.

Cuando la pelota golpeó el suelo, tenía 0 J de energía potencial y 196 J de energía cinética.

Por lo tanto, Energía Cinética Inicial KE _i =0 J y KE _f =196 J.

Por el teorema del trabajo-energía:

W _neto = ΔKE

KE _f − KE _i = 196−0

= 196J

Por lo tanto, el trabajo neto realizado sobre la pelota es 196 J.

Problema 2: Un automóvil de 500 kg de masa que viaja a una velocidad de 16 m/s aplica los frenos del automóvil en algún punto. Los frenos del automóvil proporcionan una fuerza de fricción de 4000 N. Determine la distancia de frenado del automóvil.

Solución:

Dado,

Masa del coche, m = 500 kg

Velocidad del carro, v = 16 m/s

Fuerza de fricción de los frenos, $\vec{F}$ = 4000 N

Aplicando el teorema del trabajo-energía como:

El cambio en la energía cinética es igual al trabajo realizado por la fuerza de fricción de los frenos del automóvil.

Por lo tanto, la energía cinética inicial del automóvil en el momento en que se aplicaron los frenos es,

$KE_i = \frac{1}{2}mv^2$

$KE_i = \frac{1}{2}\times500\times (16)^2$ ⇒ 64 kJ.

Como el carro está en reposo, Energía Cinética Final =0, por lo tanto $\triangle KE$ = 64 kJ. ……(1)

Considere que el desplazamiento del automóvil es ΔX. Dado que la dirección de la fuerza aplicada y el desplazamiento son direcciones opuestas, θ=180°.

Entonces el trabajo realizado viene dado por:

$W=F\triangle x cos\theta$

$W = (4000)(\triangle x)(\cos{180\degree})$

$W = -4000\triangle x$ ……(2)

Por el teorema del trabajo y la energía, el cambio en la energía cinética es igual al trabajo realizado.

$64000 = -4000 \triangle x$

$\triangle x = 16m$

Por lo tanto, la distancia de frenado del automóvil es de 16 m .

Problema 3: En un día lluvioso, el conductor de un automóvil frenó al ver una luz roja. Se mide que el automóvil se detuvo con una marca de derrape de 100 m detrás de él desde el punto de aplicación de los frenos, el coeficiente de fricción se estimó en 0,45. ¿Cuál era la velocidad del automóvil cuando el conductor frenó?

Solución:

Dado,

Desplazamiento del carro, d = 100m

Coeficiente de fricción, μ = 0,45

Sabemos que la fuerza de fricción es la causa del trabajo realizado en el automóvil para detenerlo. También sabemos que el trabajo es igual al cambio en la energía cinética.

−W=ΔKE (símbolo -ve porque la fuerza de fricción y el desplazamiento están en dirección opuesta, cos(180°)=-1)

$-W=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2$

El trabajo es igual a la fuerza por el desplazamiento sobre el que actuó la fuerza.

−W=Fd

Por lo tanto, $Fd=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2$

La fuerza en este caso es la fuerza de fricción. entonces, F _fricción = μF _N

Dado que el automóvil está en un camino nivelado, la fuerza normal es igual y opuesta a la fuerza de gravedad.

F _N = F _G

La fuerza de la gravedad es igual a la masa por la aceleración de la gravedad, F _G =mg

Por lo tanto, F _fricción = μmg

Por, ecuación trabajo-energía cinética,

$-μmgd=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2$

Como la velocidad final es 0 obtenemos,

$-μmgd=-\frac{1}{2}mv_i^2$

$μgd=\frac{1}{2}v_i^2$

$(0.45)(9.8\frac{m}{s^2})(100m)=\frac{1}{2}v_i^2$

$v_i^2=882 \frac{m}{s}$

$v_i=29.69m/s$

Por lo tanto, la velocidad inicial del automóvil es 29,69 m/s .

Problema 4: La fuerza de propulsión neta de un cohete de 2000 kg es de 600 N. El cohete acelera uniformemente desde una velocidad inicial de 50 m/s hasta una velocidad final de 80 m/s en un corto período de tiempo. Suponga que la masa del cohete permanece constante mientras quema combustible y que la fuerza neta está dirigida en la dirección del movimiento. ¿Cuánto trabajo neto se ha realizado en el cohete (en KJ)?

Solución:

Dado,

Masa del cohete, m = 2000 kg.

Fuerza de propulsión neta, F = 600 N.

Velocidad inicial del cohete, v _i = 50 m/s.

Velocidad final del cohete, v _f = 80 m/s.

Aplicando el teorema de la energía del trabajo,

W = ΔKE

La energía cinética inicial del cohete KE _i viene dada por:

$KE_i=\frac{1}{2}mv_i^2$

$KE_i= 0.5(2000kg)(50)^2=2500000J$

De manera similar, la energía cinética final del cohete KE _f está dada por,

$KE_f=\frac{1}{2}mv_f^2$

$KE_f= 0.5(2000kg)(80)^2=6400000J$

Trabajo neto realizado = El cambio en la energía cinética a las dos velocidades:

W = ΔKE

6400000−2500000 =3 900000J

Por lo tanto, el trabajo neto realizado sobre el cohete es de 3900 kJ.

Problema 5: Una flecha de 100 g se dispara con un arco cuya cuerda ejerce una fuerza promedio de 150 N sobre la flecha en una distancia de 50 cm. ¿Cuál es la velocidad de la flecha cuando sale del arco?

Solución:

Dado,

Masa de flecha, m = 100g

Fuerza ejercida sobre la flecha, F = 150N

Desplazamiento de la cuerda, d = 50 cm

Aplicando el teorema del trabajo y la energía,

W = ΔKE

$W=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2$

El trabajo es igual a la fuerza por el desplazamiento sobre el que actuó la fuerza.

W = Fd

Por lo tanto, $Fd=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2$

Sustituyendo los valores, obtenemos

$(150N)(0.5m)=\frac{1}{2}(0.01kg)(v_f)2−\frac{1}{2}(0.01kg)(0m/s)^2$

$v_f^2=15000m/s$

$v_f=122.47m/s$

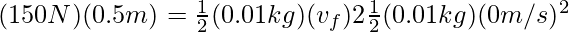
Por lo tanto, la velocidad de la flecha cuando sale del arco es de 122,47 m/s .

Problema 6: Ronaldo pateó una pelota de fútbol y viajó 50 m con una velocidad constante, ¿cuánto trabajo hace Ronaldo?

Solución:

El trabajo es el producto de una fuerza neta sobre una distancia dada.

W = F _red d

Debe haber una fuerza neta ejercida y un desplazamiento distinto de cero del objeto para que realice un trabajo.

Se proporciona el desplazamiento, pero debemos resolver para la fuerza.

De acuerdo con la Segunda Ley del Movimiento de Newton, el balón se mueve a una velocidad constante, lo que significa que su aceleración es cero.

$a=\frac{v_f−v_i}{t}$

Ya que, v _f =v _i , a=0 m/s ²

F = mamá

= metro(0)

= 0N

Si la fuerza es cero, entonces el trabajo también es cero. Por lo tanto, Trabajo realizado, W es 0 J.

Problema 7: Una caja de 20 kg se mueve a 4 m/s. Una fuerza neta de 100 N se aplica constantemente sobre la caja en la dirección de su movimiento hasta que se ha movido 25 m. ¿Cuál es la velocidad final aproximada de la caja?

Solución:

Dado,

Masa de la caja, m = 20 kg

Velocidad inicial de la caja, v _i = 4 m/s

Fuerza que actúa sobre la caja, F = 100N.

Desplazamiento de la caja, d = 25m.

Aplicando el teorema del trabajo y la energía,

W = ΔKE

$W=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2$

Trabajo realizado por el bloque, W = Fd

Ancho = 100 × 25 J

= 2500J

Energía cinética inicial, $KE_i=\frac{1}{2}mv_i^2$

$KE_i=\frac{1}{2}(20)(4 m/s)^2$

$KE_i=160 J$

Sustituyendo el valor, obtenemos,

$2500 J=\frac{1}{2}(20)v_f^2-160 J$

$v_f^2=532m/s$

$v_f=23.05m/s$

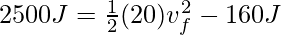
Por lo tanto, la velocidad final apropiada es 23,05 m/s.