Tiempo total requerido para recorrer un camino denotado por una string dada

Dada una ruta de string que consiste en los caracteres ‘N’, ‘S’, ‘E’ y ‘W’ que denotan 1 unidad de movimiento en las direcciones Norte, Sur, Este y Oeste respectivamente, la tarea es encontrar el tiempo necesario para recorrer la ruta completa. camino que comienza desde el origen, si toma 2 y 1 minutos para viajar en un segmento no visitado y visitado respectivamente.

Ejemplos:

Entrada: ruta = «NNES»
Salida: 8

Explicación: Dado que cada segmento se visita solo una vez, costo = 2 * 4 = 8.

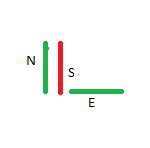
Entrada: ruta = “NSE”
Salida: 5

Explicación: 
Paso 1: Viaje al norte. Tiempo empleado = 2 minutos. 
Paso 2: viaje hacia el sur en ese mismo segmento visitado. Tiempo empleado = 1 minuto. 
Paso 3: viaje hacia el este. Tiempo empleado = 2 minutos. Por lo tanto, el tiempo total empleado = 2 + 1 + 2 = 5.

Planteamiento: La idea es usar un Set para almacenar todos los segmentos visitados y antes de visitar cada segmento, verificar si está presente en el Set o no. Siga los pasos a continuación para resolver el problema.

• Inicialice un conjunto s para almacenar un par de enteros. El conjunto almacenará todos los segmentos visitados.
• Inicialice dos enteros x = 0 e y = 0 que denotan la posición actual. Además, inicialice una variable time = 0 para almacenar el tiempo total necesario para recorrer la ruta completa.
• Atraviesa la cuerda y sigue los pasos a continuación.
  • Inicialice dos enteros p y q en x e y respectivamente.
  • Si path[i] es igual a ‘N’ incrementa y , de lo contrario si path[i] es igual a ‘S’ decrementa y, de lo contrario si path[i] es igual a ‘E’ incrementa x , de lo contrario decrementa x .
  • Compruebe si el segmento { p + x , q + y } existe en el conjunto o no . si suma 1 al valor del tiempo , de lo contrario, suma 2 al valor del tiempo.
  • Inserta el segmento { p + x , q + y } en el conjunto.
• Después de completar los pasos anteriores, imprima el valor del tiempo.

A continuación se muestra la implementación del enfoque anterior.

// C++ code for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate time
// taken to travel the path
void calcTotalTime(string path)
{
    // Stores total time
    int time = 0;
 
    // Initial position
    int x = 0, y = 0;
 
    // Stores visited segments
    set<pair<int, int> > s;
 
    for (int i = 0; i < path.size(); i++) {
 
        int p = x;
        int q = y;
 
        if (path[i] == 'N')
            y++;
 
        else if (path[i] == 'S')
            y--;
 
        else if (path[i] == 'E')
            x++;
 
        else if (path[i] == 'W')
            x--;
 
        // Check whether segment
        // is present in the set
        if (s.find({ p + x, q + y })
            == s.end()) {
            // Increment the value
            // of time by 2
            time += 2;
 
            // Insert segment into the set
            s.insert({ p + x, q + y });
        }
        else
            time += 1;
    }
 
    // Print the value
    // of time
    cout << time << endl;
}
 
// Driver Code
int main()
{
    string path = "NSE";
 
    calcTotalTime(path);
 
    return 0;
}

// Java program for above approach
import java.util.*;
 
class GFG{
 
// Function to calculate time
// taken to travel the path
static void calcTotalTime(String path)
{
     
    // Stores total time
    int time = 0;
 
    // Initial position
    int x = 0, y = 0;
 
    // Stores visited segments
    Set<String> s = new HashSet<>();
    for(int i = 0; i < path.length(); i++)
    {
        int p = x;
        int q = y;
 
        if (path.charAt(i) == 'N')
            y++;
 
        else if (path.charAt(i) == 'S')
            y--;
 
        else if (path.charAt(i) == 'E')
            x++;
 
        else if (path.charAt(i) == 'W')
            x--;
 
        // Check whether segment
        // is present in the set
        String o = (p + x) + " " + (q + y);
        if (!s.contains(o))
        {
             
            // Increment the value
            // of time by 2
            time += 2;
 
            // Insert segment into the set
            s.add(o);
        }
        else
            time += 1;
    }
 
    // Print the value
    // of time
    System.out.println(time);
}
 
// Driver Code
public static void main(String[] args)
{
    String path = "NSE";
 
    calcTotalTime(path);
}
}
 
// This code is contributed by Hritik

# Python 3 code for the above approach
 
# Function to calculate time
# taken to travel the path
def calcTotalTime(path):
 
    # Stores total time
    time = 0
 
    # Initial position
    x = 0
    y = 0
 
    # Stores visited segments
    s = set([])
 
    for i in range(len(path)):
 
        p = x
        q = y
 
        if (path[i] == 'N'):
            y += 1
 
        elif (path[i] == 'S'):
            y -= 1
 
        elif (path[i] == 'E'):
            x += 1
 
        elif (path[i] == 'W'):
            x -= 1
 
        # Check whether segment
        # is present in the set
        if (p + x, q + y) not in s:
            # Increment the value
            # of time by 2
            time += 2
 
            # Insert segment into the set
            s.add((p + x, q + y))
 
        else:
            time += 1
 
    # Print the value
    # of time
    print(time)
 
 
# Driver Code
if __name__ == "__main__":
 
    path = "NSE"
 
    calcTotalTime(path)
 
    # This code is contributed by ukasp.

// C# program for the above approach
using System;
using System.Collections.Generic;
 
class GFG{
 
// Function to calculate time
// taken to travel the path
static void calcTotalTime(string path)
{
     
    // Stores total time
    int time = 0;
 
    // Initial position
    int x = 0, y = 0;
 
    // Stores visited segments
    HashSet<string> s = new HashSet<string>();
    for(int i = 0; i < path.Length; i++)
    {
        int p = x;
        int q = y;
 
        if (path[i] == 'N')
            y++;
 
        else if (path[i] == 'S')
            y--;
 
        else if (path[i] == 'E')
            x++;
 
        else if (path[i] == 'W')
            x--;
 
        // Check whether segment
        // is present in the set
        string o = (p + x) + " " + (q + y);
        if (s.Contains(o) == false)
        {
             
            // Increment the value
            // of time by 2
            time += 2;
 
            // Insert segment into the set
            s.Add(o);
        }
        else
            time += 1;
    }
 
    // Print the value
    // of time
    Console.Write(time);
}
 
// Driver Code
public static void Main()
{
    string path = "NSE";
 
    calcTotalTime(path);
}
}
 
// This code is contributed by bgangwar59

<script>
 
// Javascript code for the above approach
 
// Function to calculate time
// taken to travel the path
function calcTotalTime(path)
{
     
    // Stores total time
    var time = 0;
 
    // Initial position
    var x = 0, y = 0;
 
    // Stores visited segments
    var s = new Set();
 
    for(var i = 0; i < path.length; i++)
    {
        var p = x;
        var q = y;
 
        if (path[i] == 'N')
            y++;
 
        else if (path[i] == 'S')
            y--;
 
        else if (path[i] == 'E')
            x++;
 
        else if (path[i] == 'W')
            x--;
 
        // Check whether segment
        // is present in the set
        if (!s.has([p + x, q + y].toString()))
        {
             
            // Increment the value
            // of time by 2
            time += 2;
 
            // Insert segment into the set
            s.add([p + x, q + y].toString());
        }
        else
            time += 1;
    }
 
    // Print the value
    // of time
    document.write(time)
}
 
// Driver Code
var path = "NSE";
 
calcTotalTime(path);
 
</script>

5

Complejidad temporal: O(NlogN)
Espacio auxiliar: O(N)