Clasificación de cuentas | Un algoritmo de clasificación natural

También conocido como Gravity sort, este algoritmo se inspiró en fenómenos naturales y se diseñó teniendo en cuenta los objetos (o cuentas) que caen bajo la influencia de la gravedad.

La idea: los números positivos están representados por un conjunto de cuentas como las de un ábaco.

Clasificación de {7, 2, 1, 4, 2} usando Bead Sort. Las cuentas caen una por una si hay espacio debajo.

1. Como en la imagen de arriba, las cuentas representan los siguientes números de arriba a abajo: 7, 2, 1, 4, 2. Ahora, imagina que esta es la posición de las cuentas en el tiempo t = 0 y con cada segundo que pasa, las cuentas caer un nivel siempre que no haya una cuenta debajo de ellos. En tal caso, simplemente descansan sobre la cuenta debajo de ellos. (Las varillas están numeradas de izquierda a derecha y los niveles están numerados desde abajo como 1, 2, ………. n.)
2. Ahora, en el tiempo t = 1 , las 2 cuentas inferiores de las dos primeras barras de la izquierda permanecen en sus posiciones mientras que la segunda cuenta de la parte superior de la segunda barra desciende un nivel para descansar sobre la cuenta de abajo. Las cuentas de la 3.ª y 4.ª barra del nivel 2 bajan al nivel 1. Al mismo tiempo, las cuentas de las barras 3 a 7 bajan un nivel. Ahora, los números de arriba a abajo se convierten en: 2, 6, 2, 2, 4.
3. Esto continúa hasta el momento t = 4 , donde obtenemos la secuencia ordenada de números de arriba a abajo, que es: 1, 2, 2, 4, 7.

¿Por qué se llama así?

Cuando uno intenta visualizar este algoritmo, parece como si las cuentas cayeran bajo la influencia de la gravedad hasta el nivel más bajo que pueden alcanzar, lo que da como resultado que el conjunto de cuentas se organice en orden descendente desde el suelo hacia arriba. Si tiene problemas para visualizar esto, visite este enlace

Digamos que tenemos que ordenar los números 3, 4, 1, 2. El algoritmo anterior funcionaría así.

Trabajo de clasificación de cuentas

A continuación se muestra el código, intente implementarlo usted mismo antes de mirar el código.

El código:

// C++ program to implement gravity/bead sort
#include <bits/stdc++.h>
using namespace std;
  
#define BEAD(i, j) beads[i * max + j]
  
// function to perform the above algorithm
void beadSort(int *a, int len)
{
    // Find the maximum element
    int max = a[0];
    for (int i = 1; i < len; i++)
        if (a[i] > max)
           max = a[i];
  
    // allocating memory
    unsigned char beads[max*len];
    memset(beads, 0, sizeof(beads));
  
    // mark the beads
    for (int i = 0; i < len; i++)
        for (int j = 0; j < a[i]; j++)
            BEAD(i, j) = 1;
  
    for (int j = 0; j < max; j++)
    {
        // count how many beads are on each post
        int sum = 0;
        for (int i=0; i < len; i++)
        {
            sum += BEAD(i, j);
            BEAD(i, j) = 0;
        }
  
        // Move beads down
        for (int i = len - sum; i < len; i++)
            BEAD(i, j) = 1;
    }
  
    // Put sorted values in array using beads
    for (int i = 0; i < len; i++)
    {
        int j;
        for (j = 0; j < max && BEAD(i, j); j++);
  
        a[i] = j;
    }
}
  
// driver function to test the algorithm
int main()
{
    int a[] = {5, 3, 1, 7, 4, 1, 1, 20};
    int len = sizeof(a)/sizeof(a[0]);
  
    beadSort(a, len);
  
    for (int i = 0; i < len; i++)
        printf("%d ", a[i]);
  
    return 0;
}

Producción:

1 1 1 3 4 5 7 20

Complejidad del tiempo:
la complejidad del tiempo de ejecución del algoritmo varía de O(1) a O(S) (S es la suma de los números enteros de entrada) según la perspectiva del usuario. Finalmente, se sugieren tres posibles implementaciones.

1. O(1)  : Dejar caer todas las perl juntas como una sola operación (simultánea). Esta complejidad no se puede implementar en la práctica.
2. O( 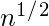): En un modelo físico realista que utiliza la gravedad, el tiempo que tardan en dejar caer las cuentas es proporcional a la raíz cuadrada de la altura máxima, que es proporcional a n.
3. O(n)  : Dejar caer la fila de cuentas en el marco (que representa un número) como una operación distinta ya que el número de filas es igual a n.
4. O(S)  : Dejar caer todas y cada una de las cuentas como una operación separada ya que S es la suma de todas las cuentas.

Al igual que la ordenación de Pigeonhole, la ordenación de cuentas es inusual porque, en el peor de los casos, puede funcionar más rápido que O( ), el rendimiento más rápido posible para una ordenación de comparación en el peor de los casos. Esto es posible porque la clave para una ordenación de cuentas es siempre un número entero positivo y la ordenación de cuentas explota su estructura.

Complejidad espacial: la clasificación de perl es el poseedor del récord en cuanto a residuos. Los costos de la memoria adicional superan los costos de almacenamiento de la propia array. Su complejidad de memoria es O( )

Referencias:

• https://www.wikiwand.com/en/Bead_sort
• https://kukuruku.co/post/bead-sort/
• https://rosettacode.org/wiki/Sorting_algorithms/Bead_sort
• https://www.cs.auckland.ac.nz/~mjd/misc/BeadSort5.pdf

Este artículo es una contribución de Palash Nigam . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.