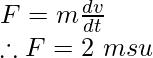Un cuerpo en reposo sigue estando en reposo sin que se aplique ninguna fuerza externa. Sin embargo, cuando se aplica una fuerza a un objeto, tiende a moverse en la dirección de la fuerza aplicada, y entonces se dice que la fuerza realiza trabajo. El trabajo realizado por la fuerza sobre cualquier objeto es matemáticamente equivalente al producto de la fuerza y el desplazamiento del objeto que se produce en la dirección de la fuerza.
El trabajo realizado por la fuerza depende solo de las posiciones inicial y final del cuerpo, es decir, del desplazamiento, y no del camino real seguido entre las posiciones inicial y final. Por lo tanto, cuando un objeto se desplaza una pequeña distancia, digamos s, bajo la influencia de una fuerza constante F, el trabajo realizado por la fuerza es equivalente a,
W = F × s = F s porque θ
donde θ es el ángulo más pequeño entre F y s.
La unidad SI de trabajo realizado es Joule (J) . Es una cantidad escalar , que solo tiene magnitud y no dirección. Su fórmula dimensional es [ML 2 T -2 ] .
El trabajo realizado por una fuerza sobre cualquier objeto es equivalente a cero, si
- El cuerpo no se desplaza realmente, es decir, s = 0.
- El cuerpo se desplaza perpendicularmente a la dirección de la fuerza, es decir, el ángulo entre la fuerza y el desplazamiento es θ = 90°
La energía es la forma de vida fundamental para todos los seres vivos. El Sol en este universo es considerado como la forma elemental de energía en el planeta Tierra. La energía se refiere a la capacidad de cualquier objeto para realizar un trabajo. Se requiere energía para realizar el trabajo. Es una propiedad cualitativa de un cuerpo. La ley de conservación de la energía establece que la energía no se crea ni se destruye. Simplemente se puede transferir de un medio a otro.
La unidad SI de energía es Joule (J) . Es una cantidad escalar , que solo tiene magnitud y no dirección. Su fórmula dimensional es [ML 2 T -2 ] .
La potencia se refiere a la tasa de tiempo del trabajo realizado por un objeto. Matemáticamente,
Potencia = Tasa de trabajo realizado = Trabajo realizado / Tiempo empleado
Por lo tanto, cuando un objeto se desplaza una pequeña distancia, digamos s, bajo la influencia de una fuerza constante F, el trabajo realizado por la potencia es equivalente a,
PAGS = W / T = F × s / T
Pero, s/t = v, velocidad del cuerpo.
Por lo tanto,
PAGS = F × v = F v cos θ
donde θ es el ángulo más pequeño entre F y v.
La unidad SI de energía es Watt (W). Es una cantidad escalar, que solo tiene magnitud y no dirección, ya que es solo una relación de dos cantidades escalares. Su fórmula dimensional es [ML 2 T -3 ].
¿Qué es Colisión?
Una colisión es un evento donde una fuerza fuerte actúa por un lapso de tiempo muy corto entre dos o más cuerpos. Una colisión es un evento aislado. La energía y el momento de las partículas que interactúan sufren un cambio como resultado de la colisión. La colisión puede ocurrir por contacto físico real de los cuerpos involucrados, por ejemplo, la colisión entre dos bolas de billar o una bola y un bate. Puede haber colisiones donde no hay contacto físico real, por ejemplo, la colisión de las partículas alfa por un núcleo.
Cualquier colisión está guiada por tres etapas identificables distintas, es decir, antes, durante y después. Antes de la colisión, las fuerzas de interacción entre las partículas son cero, ya que las partículas son independientes. Además, después de la colisión, la fuerza vuelve a ser cero. Durante la colisión, las partículas entran en contacto entre sí, por lo tanto, la fuerza de interacción se vuelve muy grande. El movimiento de los cuerpos está guiado por las fuerzas dominantes. Dado que, en la mayoría de los casos prácticos, se desconoce la magnitud de la fuerza que interactúa, la segunda ley del movimiento de Newton no se puede utilizar en tales casos. Las velocidades inicial y final se pueden calcular usando la ley de conservación del momento.
Por ejemplo, considere dos cuerpos con masas m 1 y m 2 , moviéndose con velocidades u 1 y u 2 . Sufren una colisión debido a la aplicación de una fuerza externa F ext durante un pequeño intervalo de tiempo y luego las velocidades finales se vuelven v 1 y v 2 .

Conservación de la cantidad de movimiento y la conservación de la energía durante una colisión
De acuerdo con las leyes fundamentales de la física, ciertos atributos son aplicables para cualquier tipo de colisión:
- Conservación de la cantidad de movimiento: la colisión tiene lugar durante un intervalo de tiempo muy pequeño, y durante este período la fuerza impulsiva promedio que causa la colisión es significativamente mayor que la fuerza externa que actúa sobre el sistema. Por lo tanto, durante una colisión, la aplicación de fuerzas externas, como las fuerzas de fricción o gravitatorias, no se tienen en cuenta. Esta fuerza impulsiva es de naturaleza interna, por lo tanto, la cantidad de movimiento total del sistema permanece constante para todos los efectos prácticos. Por lo tanto, permanece conservado en todo el sistema.
- Conservación de la energía: De acuerdo con la ley de conservación de la energía, la energía no se puede destruir ni crear. Sólo se puede transferir de un medio a otro. Por lo tanto, la energía total durante una colisión siempre se conserva. La energía total incluye todas las formas plausibles de energía creadas y destruidas durante una colisión, como la energía mecánica, la energía interna, la energía de excitación y la energía de masa.
Tipos de colisión
Durante la colisión, los cuerpos que interactúan entran en contacto inmediato entre sí debido a que ejercen fuerzas. Esta actividad se lleva a cabo durante un período de tiempo muy corto. Hay dos tipos de colisiones, a saber:
- Sobre la base de la conservación de la energía cinética.
- Colisión perfectamente elástica
- Colisión inelástica
- Colisión perfectamente inelástica
|
Parámetro |
Colisión perfectamente elástica |
Colisión inelástica |
Colisión perfectamente inelástica |
| Definición |
La energía cinética después del choque es igual a la energía cinética antes del choque. |
La energía cinética después del choque no es igual a la energía cinética antes del choque. |
En esta colisión, dos cuerpos quedan pegados o se mueven con la misma velocidad después de la colisión. |
| Coeficiente de restitución |
mi = 1 |
0 < mi < 1 |
mi = 0 |
| Energías cinéticas |
(KE) final = (KE) inicial |
|
Hay una gran pérdida de energía cinética. |
| Ejemplo |
La colisión entre partículas atómicas. |
La colisión entre dos vehículos en una carretera. |
Disparo de una bala que queda incrustada en un bloque de madera. |
- Sobre la base de la dirección de los cuerpos que chocan
- Colisión frontal o unidimensional
- colisión oblicua
| Parámetro |
Colisión frontal o unidimensional |
colisión oblicua |
| Definición | El movimiento de las partículas que chocan o interactúan antes y después de la colisión actúa a lo largo de la misma línea que la colisión. |
El movimiento de las partículas que chocan o interactúan antes y después de la colisión no actúa a lo largo de la misma línea que la colisión. Si las partículas que interactúan antes y después de la colisión permanecen en el mismo plano, entonces la colisión oblicua se denomina bidimensional; de lo contrario, se denomina colisión tridimensional. |
| Parámetro de impacto |
El parámetro de impacto b es cero para este tipo de colisión
|
El parámetro de impacto b se encuentra entre 0 y (r 1 + r 2 ), es decir, 0 < b < (r 1 + r 2 ) donde r 1 y r 2 son radios de cuerpos en colisión.
|
| Ejemplo | Colisión de dos planeadores en una pista de aire. | Colisión de las bolas de billar. |
Colisión frontal perfectamente elástica
Supongamos que dos cuerpos de masas m 1 y m 2 se mueven con velocidades iniciales u 1 y u 2 en la misma dirección y chocan de tal manera que después de la colisión sus velocidades finales son v 1 y v 2 respectivamente.
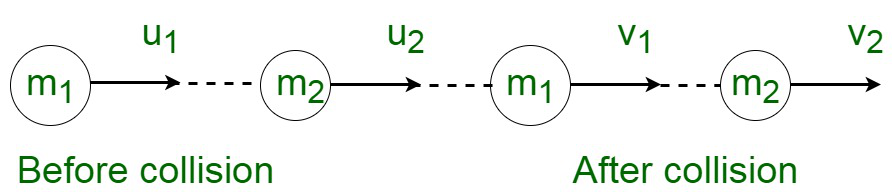
Según la ley de conservación de la cantidad de movimiento
metro 1 tu 1 + metro 2 tu 2 = metro 1 v 1 + metro 2 v 2 …………(1)
⇒ metro 1 (u 1 – v 1 ) = metro 2 (v 2 – tu 2 ) ………..(2)
De acuerdo con la ley de conservación de la energía cinética, tenemos,
……..(3)
⇒
………(4)
Dividiendo la ecuación (4) por la ecuación (2)
v 1 + tu 1 = v 2 + tu 2 ……….(5)
⇒ tu 1 – tu 2 = v 2 – v 1 ………..(6)
Sabemos,
Velocidad relativa de aproximación = Velocidad relativa de separación
Derivando de la ecuación (5) obtenemos
v 2 = v 1 + tu 1 – tu 2
Sustituyendo este valor de v 2 en la ecuación (i) y reorganizando obtenemos
…….(7)
Similarmente,
……….(8)
Colisión oblicua perfectamente elástica
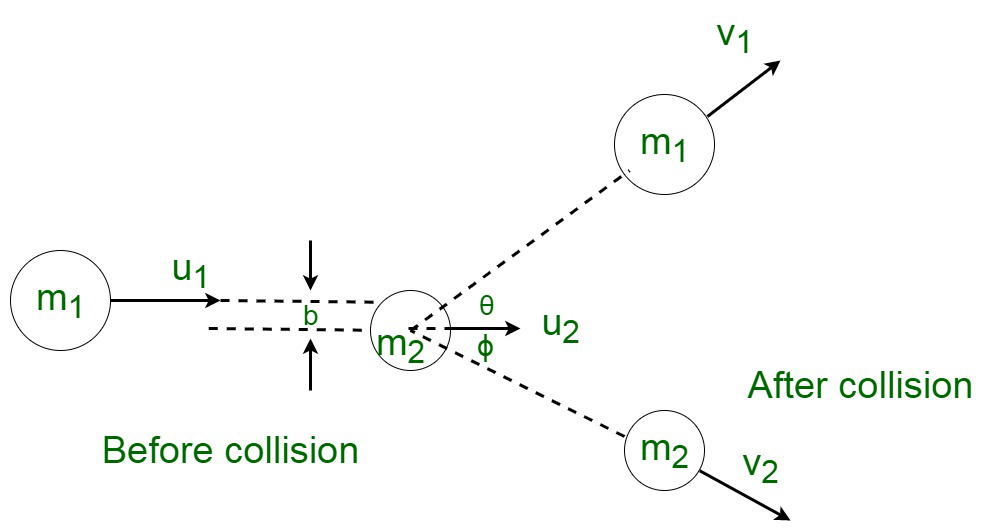
Supongamos dos cuerpos en movimiento,
Por la ley de conservación de la cantidad de movimiento,
Tenemos,
A lo largo del eje x,
metro 1 tu 2 + metro 2 tu 2 = metro 1 v 1 cosθ + metro 2 v 2 cosϕ ……..(1)
A lo largo del eje y,
0 = metro 1 v 1 senθ – metro 2 v 2 senϕ ………(2)
Sabemos,
Por la ley de conservación de la energía cinética:
……..(3)
Problemas Resueltos
Problema 1: Supongamos que, s pequeñas bolas, cada una de masa m golpean una superficie elásticamente cada segundo con una velocidad um/s. Calcular la fuerza atestiguada por la superficie.
Solución:
Dado que hay un rebote de la pelota con velocidad no modificada, por lo tanto,
El cambio de velocidad = 2u
Masa que choca con la superficie = sm
La fuerza experimentada por la superficie está dada por,
Problema 2: Inicialmente, un automóvil de 400 kg de masa que viaja con una velocidad de 72 kmph choca accidentalmente contra un automóvil de 4000 kg de masa. Antes de la colisión, el camión viajaba a una velocidad de 9 km/h, en la misma dirección que el automóvil. Como resultado de la colisión, el automóvil retrocede con una velocidad de 18 km/h. Calcule la velocidad con la que se mueve el camión después de la colisión.
Solución:
Por la ley de conservación del momento lineal, tenemos,
La suma del momento inicial es equivalente a la suma del momento final.
metro 1 tu 1 + metro 1 tu 2 = metro 1 v 1 + metro 2 v 2
⇒ 400 × 72 + 4000 × 9 = 400 × (-18) + 4000 × v 2
⇒ v2 = 18 km/h
Por lo tanto, la velocidad final del automóvil es de 18 km/h.
Problema 3: Una caja se mantiene en el origen de masa equivalente a 5 kg. Se le aplica una fuerza de 10 N para simular su movimiento en un ángulo de 60° con el eje x. Como resultado de este desplazamiento, la caja se mueve 4 m. ¿Cuál es el trabajo realizado por la aplicación de la fuerza?
Solución:
El trabajo realizado viene dado por el producto escalar de la fuerza y el desplazamiento, es decir,
Fs = Fs cos θ
=10 × 4 × cos 60°
= 20J
Problema 4: Una caja se mantiene sobre una mesa de masa equivalente a 1 kg. Se arrastra a lo largo de la mesa horizontal a lo largo de 1 m por una fuerza externa de 8 N. Luego se somete a una altura vertical de 2 m. Calcule el trabajo neto realizado.
Solución:
Trabajo realizado para desplazar la caja horizontalmente, W H
= F × s
= 8 × 1 = 8J
Trabajo realizado para elevar la caja verticalmente, W v = F × s
= mxgxh
= 1 × 10 × 2 = 20J
Por lo tanto,
El trabajo neto realizado sobre la caja es W H + W v
= 8 +20 = 28J
Problema 5: Se requiere una fuerza horizontal de 5 N para mantener una velocidad de 2 m/s para un bloque de 10 kg de masa que se desliza sobre una superficie rugosa. ¿El trabajo realizado por esta fuerza en un minuto es?
Solución:
Matemáticamente,
Trabajo realizado por un objeto = Fuerza × desplazamiento
⇒ W = F × s
Ya que, sabemos,
s = vxt
= F × v × t
= 5 × 2 × 60
= 600J
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA