La Torre de Hanoi es un rompecabezas matemático. Consta de tres postes y una serie de discos de diferentes tamaños que pueden deslizarse sobre cualquier poste. El rompecabezas comienza con el disco en una pila ordenada en orden ascendente de tamaño en un polo, el más pequeño en la parte superior, formando así una forma cónica. El objetivo del rompecabezas es mover todos los discos de un polo (digamos ‘polo de origen’) a otro polo (digamos ‘polo de destino’) con la ayuda del tercer polo (digamos polo auxiliar).
El rompecabezas tiene las siguientes dos reglas:
1. No puedes colocar un disco más grande en un disco más pequeño
2. Solo se puede mover un disco a la vez
Ya hemos discutido una solución recursiva para la Torre de Hanoi . También hemos visto que para n discos, se requieren un total de 2 n – 1 movimientos.
Algoritmo iterativo:
1. Calculate the total number of moves required i.e. "pow(2, n)
- 1" here n is number of disks.
2. If number of disks (i.e. n) is even then interchange destination
pole and auxiliary pole.
3. for i = 1 to total number of moves:
if i%3 == 1:
legal movement of top disk between source pole and
destination pole
if i%3 == 2:
legal movement top disk between source pole and
auxiliary pole
if i%3 == 0:
legal movement top disk between auxiliary pole
and destination pole
Ejemplo:
Let us understand with a simple example with 3 disks: So, total number of moves required = 7

S A D When i= 1, (i % 3 == 1) legal movement between‘S’ and ‘D’

When i = 2, (i % 3 == 2) legal movement between ‘S’ and ‘A’

When i = 3, (i % 3 == 0) legal movement between ‘A’ and ‘D’ ’
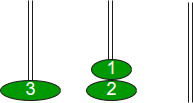
When i = 4, (i % 3 == 1) legal movement between ‘S’ and ‘D’

When i = 5, (i % 3 == 2) legal movement between ‘S’ and ‘A’

When i = 6, (i % 3 == 0) legal movement between ‘A’ and ‘D’

When i = 7, (i % 3 == 1) legal movement between ‘S’ and ‘D’

Entonces, después de que todos estos polos de destino contengan todos los en orden de tamaño.
Después de observar las iteraciones anteriores, podemos pensar que después de mover un disco que no sea el disco más pequeño, el próximo disco que se mueva debe ser el disco más pequeño porque es el disco superior que descansa sobre el polo de repuesto y no hay otras opciones para mover. un disco
C++
// C++ Program for Iterative Tower of Hanoi
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// A structure to represent a stack
struct Stack
{
unsigned capacity;
int top;
int *array;
};
// function to create a stack of given capacity.
struct Stack* createStack(unsigned capacity)
{
struct Stack* stack =
(struct Stack*) malloc(sizeof(struct Stack));
stack -> capacity = capacity;
stack -> top = -1;
stack -> array =
(int*) malloc(stack -> capacity * sizeof(int));
return stack;
}
// Stack is full when top is equal to the last index
int isFull(struct Stack* stack)
{
return (stack->top == stack->capacity - 1);
}
// Stack is empty when top is equal to -1
int isEmpty(struct Stack* stack)
{
return (stack->top == -1);
}
// Function to add an item to stack. It increases
// top by 1
void push(struct Stack *stack, int item)
{
if (isFull(stack))
return;
stack -> array[++stack -> top] = item;
}
// Function to remove an item from stack. It
// decreases top by 1
int pop(struct Stack* stack)
{
if (isEmpty(stack))
return INT_MIN;
return stack -> array[stack -> top--];
}
//Function to show the movement of disks
void moveDisk(char fromPeg, char toPeg, int disk)
{
cout <<"Move the disk " << disk <<" from " << fromPeg << " to "<< toPeg << endl;
}
// Function to implement legal movement between
// two poles
void moveDisksBetweenTwoPoles(struct Stack *src,
struct Stack *dest, char s, char d)
{
int pole1TopDisk = pop(src);
int pole2TopDisk = pop(dest);
// When pole 1 is empty
if (pole1TopDisk == INT_MIN)
{
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When pole2 pole is empty
else if (pole2TopDisk == INT_MIN)
{
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
// When top disk of pole1 > top disk of pole2
else if (pole1TopDisk > pole2TopDisk)
{
push(src, pole1TopDisk);
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When top disk of pole1 < top disk of pole2
else
{
push(dest, pole2TopDisk);
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
}
//Function to implement TOH puzzle
void tohIterative(int num_of_disks, struct Stack
*src, struct Stack *aux,
struct Stack *dest)
{
int i, total_num_of_moves;
char s = 'S', d = 'D', a = 'A';
//If number of disks is even, then interchange
//destination pole and auxiliary pole
if (num_of_disks % 2 == 0)
{
char temp = d;
d = a;
a = temp;
}
total_num_of_moves = pow(2, num_of_disks) - 1;
//Larger disks will be pushed first
for (i = num_of_disks; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_num_of_moves; i++)
{
if (i % 3 == 1)
moveDisksBetweenTwoPoles(src, dest, s, d);
else if (i % 3 == 2)
moveDisksBetweenTwoPoles(src, aux, s, a);
else if (i % 3 == 0)
moveDisksBetweenTwoPoles(aux, dest, a, d);
}
}
// Driver Program
int main()
{
// Input: number of disks
unsigned num_of_disks = 3;
struct Stack *src, *dest, *aux;
// Create three stacks of size 'num_of_disks'
// to hold the disks
src = createStack(num_of_disks);
aux = createStack(num_of_disks);
dest = createStack(num_of_disks);
tohIterative(num_of_disks, src, aux, dest);
return 0;
}
// This code is contributed by shivanisinghss2110
C
// C Program for Iterative Tower of Hanoi
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <limits.h>
// A structure to represent a stack
struct Stack
{
unsigned capacity;
int top;
int *array;
};
// function to create a stack of given capacity.
struct Stack* createStack(unsigned capacity)
{
struct Stack* stack =
(struct Stack*) malloc(sizeof(struct Stack));
stack -> capacity = capacity;
stack -> top = -1;
stack -> array =
(int*) malloc(stack -> capacity * sizeof(int));
return stack;
}
// Stack is full when top is equal to the last index
int isFull(struct Stack* stack)
{
return (stack->top == stack->capacity - 1);
}
// Stack is empty when top is equal to -1
int isEmpty(struct Stack* stack)
{
return (stack->top == -1);
}
// Function to add an item to stack. It increases
// top by 1
void push(struct Stack *stack, int item)
{
if (isFull(stack))
return;
stack -> array[++stack -> top] = item;
}
// Function to remove an item from stack. It
// decreases top by 1
int pop(struct Stack* stack)
{
if (isEmpty(stack))
return INT_MIN;
return stack -> array[stack -> top--];
}
//Function to show the movement of disks
void moveDisk(char fromPeg, char toPeg, int disk)
{
printf("Move the disk %d from \'%c\' to \'%c\'\n",
disk, fromPeg, toPeg);
}
// Function to implement legal movement between
// two poles
void moveDisksBetweenTwoPoles(struct Stack *src,
struct Stack *dest, char s, char d)
{
int pole1TopDisk = pop(src);
int pole2TopDisk = pop(dest);
// When pole 1 is empty
if (pole1TopDisk == INT_MIN)
{
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When pole2 pole is empty
else if (pole2TopDisk == INT_MIN)
{
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
// When top disk of pole1 > top disk of pole2
else if (pole1TopDisk > pole2TopDisk)
{
push(src, pole1TopDisk);
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When top disk of pole1 < top disk of pole2
else
{
push(dest, pole2TopDisk);
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
}
//Function to implement TOH puzzle
void tohIterative(int num_of_disks, struct Stack
*src, struct Stack *aux,
struct Stack *dest)
{
int i, total_num_of_moves;
char s = 'S', d = 'D', a = 'A';
//If number of disks is even, then interchange
//destination pole and auxiliary pole
if (num_of_disks % 2 == 0)
{
char temp = d;
d = a;
a = temp;
}
total_num_of_moves = pow(2, num_of_disks) - 1;
//Larger disks will be pushed first
for (i = num_of_disks; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_num_of_moves; i++)
{
if (i % 3 == 1)
moveDisksBetweenTwoPoles(src, dest, s, d);
else if (i % 3 == 2)
moveDisksBetweenTwoPoles(src, aux, s, a);
else if (i % 3 == 0)
moveDisksBetweenTwoPoles(aux, dest, a, d);
}
}
// Driver Program
int main()
{
// Input: number of disks
unsigned num_of_disks = 3;
struct Stack *src, *dest, *aux;
// Create three stacks of size 'num_of_disks'
// to hold the disks
src = createStack(num_of_disks);
aux = createStack(num_of_disks);
dest = createStack(num_of_disks);
tohIterative(num_of_disks, src, aux, dest);
return 0;
}
Java
// Java program for iterative
// Tower of Hanoi
class TOH{
// A structure to represent a stack
class Stack
{
int capacity;
int top;
int array[];
}
// Function to create a stack of given capacity.
Stack createStack(int capacity)
{
Stack stack = new Stack();
stack.capacity = capacity;
stack.top = -1;
stack.array = new int[capacity];
return stack;
}
// Stack is full when the top is equal
// to the last index
boolean isFull(Stack stack)
{
return (stack.top == stack.capacity - 1);
}
// Stack is empty when top is equal to -1
boolean isEmpty(Stack stack)
{
return (stack.top == -1);
}
// Function to add an item to stack.It
// increases top by 1
void push(Stack stack, int item)
{
if (isFull(stack))
return;
stack.array[++stack.top] = item;
}
// Function to remove an item from stack.It
// decreases top by 1
int pop(Stack stack)
{
if (isEmpty(stack))
return Integer.MIN_VALUE;
return stack.array[stack.top--];
}
// Function to implement legal movement between
// two poles
void moveDisksBetweenTwoPoles(Stack src, Stack dest,
char s, char d)
{
int pole1TopDisk = pop(src);
int pole2TopDisk = pop(dest);
// When pole 1 is empty
if (pole1TopDisk == Integer.MIN_VALUE)
{
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When pole2 pole is empty
else if (pole2TopDisk == Integer.MIN_VALUE)
{
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
// When top disk of pole1 > top disk of pole2
else if (pole1TopDisk > pole2TopDisk)
{
push(src, pole1TopDisk);
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When top disk of pole1 < top disk of pole2
else
{
push(dest, pole2TopDisk);
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
}
// Function to show the movement of disks
void moveDisk(char fromPeg, char toPeg, int disk)
{
System.out.println("Move the disk " + disk +
" from " + fromPeg +
" to " + toPeg);
}
// Function to implement TOH puzzle
void tohIterative(int num_of_disks, Stack
src, Stack aux, Stack dest)
{
int i, total_num_of_moves;
char s = 'S', d = 'D', a = 'A';
// If number of disks is even, then
// interchange destination pole and
// auxiliary pole
if (num_of_disks % 2 == 0)
{
char temp = d;
d = a;
a = temp;
}
total_num_of_moves = (int)(Math.pow(
2, num_of_disks) - 1);
// Larger disks will be pushed first
for(i = num_of_disks; i >= 1; i--)
push(src, i);
for(i = 1; i <= total_num_of_moves; i++)
{
if (i % 3 == 1)
moveDisksBetweenTwoPoles(src, dest, s, d);
else if (i % 3 == 2)
moveDisksBetweenTwoPoles(src, aux, s, a);
else if (i % 3 == 0)
moveDisksBetweenTwoPoles(aux, dest, a, d);
}
}
// Driver code
public static void main(String[] args)
{
// Input: number of disks
int num_of_disks = 3;
TOH ob = new TOH();
Stack src, dest, aux;
// Create three stacks of size 'num_of_disks'
// to hold the disks
src = ob.createStack(num_of_disks);
dest = ob.createStack(num_of_disks);
aux = ob.createStack(num_of_disks);
ob.tohIterative(num_of_disks, src, aux, dest);
}
}
// This code is contributed by Sumit Ghosh
Python3
# Python3 program for iterative Tower of Hanoi
import sys
# A structure to represent a stack
class Stack:
# Constructor to set the data of
# the newly created tree node
def __init__(self, capacity):
self.capacity = capacity
self.top = -1
self.array = [0]*capacity
# function to create a stack of given capacity.
def createStack(capacity):
stack = Stack(capacity)
return stack
# Stack is full when top is equal to the last index
def isFull(stack):
return (stack.top == (stack.capacity - 1))
# Stack is empty when top is equal to -1
def isEmpty(stack):
return (stack.top == -1)
# Function to add an item to stack.
# It increases top by 1
def push(stack, item):
if(isFull(stack)):
return
stack.top+=1
stack.array[stack.top] = item
# Function to remove an item from stack.
# It decreases top by 1
def Pop(stack):
if(isEmpty(stack)):
return -sys.maxsize
Top = stack.top
stack.top-=1
return stack.array[Top]
# Function to implement legal
# movement between two poles
def moveDisksBetweenTwoPoles(src, dest, s, d):
pole1TopDisk = Pop(src)
pole2TopDisk = Pop(dest)
# When pole 1 is empty
if (pole1TopDisk == -sys.maxsize):
push(src, pole2TopDisk)
moveDisk(d, s, pole2TopDisk)
# When pole2 pole is empty
else if (pole2TopDisk == -sys.maxsize):
push(dest, pole1TopDisk)
moveDisk(s, d, pole1TopDisk)
# When top disk of pole1 > top disk of pole2
else if (pole1TopDisk > pole2TopDisk):
push(src, pole1TopDisk)
push(src, pole2TopDisk)
moveDisk(d, s, pole2TopDisk)
# When top disk of pole1 < top disk of pole2
else:
push(dest, pole2TopDisk)
push(dest, pole1TopDisk)
moveDisk(s, d, pole1TopDisk)
# Function to show the movement of disks
def moveDisk(fromPeg, toPeg, disk):
print("Move the disk", disk, "from '", fromPeg, "' to '", toPeg, "'")
# Function to implement TOH puzzle
def tohIterative(num_of_disks, src, aux, dest):
s, d, a = 'S', 'D', 'A'
# If number of disks is even, then interchange
# destination pole and auxiliary pole
if (num_of_disks % 2 == 0):
temp = d
d = a
a = temp
total_num_of_moves = int(pow(2, num_of_disks) - 1)
# Larger disks will be pushed first
for i in range(num_of_disks, 0, -1):
push(src, i)
for i in range(1, total_num_of_moves + 1):
if (i % 3 == 1):
moveDisksBetweenTwoPoles(src, dest, s, d)
else if (i % 3 == 2):
moveDisksBetweenTwoPoles(src, aux, s, a)
else if (i % 3 == 0):
moveDisksBetweenTwoPoles(aux, dest, a, d)
# Input: number of disks
num_of_disks = 3
# Create three stacks of size 'num_of_disks'
# to hold the disks
src = createStack(num_of_disks)
dest = createStack(num_of_disks)
aux = createStack(num_of_disks)
tohIterative(num_of_disks, src, aux, dest)
# This code is contributed by divyeshrabadiya07.
C#
// C# program for iterative
// Tower of Hanoi
using System;
class GFG
{
// A structure to represent a stack
public class Stack
{
public int capacity;
public int top;
public int []array;
}
// function to create a stack of given capacity.
Stack createStack(int capacity)
{
Stack stack = new Stack();
stack.capacity = capacity;
stack.top = -1;
stack.array = new int[capacity];
return stack;
}
// Stack is full when top is equal to the last index
Boolean isFull(Stack stack)
{
return (stack.top == stack.capacity - 1);
}
// Stack is empty when top is equal to -1
Boolean isEmpty(Stack stack)
{
return (stack.top == -1);
}
// Function to add an item to stack.
// It increases top by 1
void push(Stack stack,int item)
{
if(isFull(stack))
return;
stack.array[++stack.top] = item;
}
// Function to remove an item from stack.
// It decreases top by 1
int pop(Stack stack)
{
if(isEmpty(stack))
return int.MinValue;
return stack.array[stack.top--];
}
// Function to implement legal
// movement between two poles
void moveDisksBetweenTwoPoles(Stack src, Stack dest,
char s, char d)
{
int pole1TopDisk = pop(src);
int pole2TopDisk = pop(dest);
// When pole 1 is empty
if (pole1TopDisk == int.MinValue)
{
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When pole2 pole is empty
else if (pole2TopDisk == int.MinValue)
{
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
// When top disk of pole1 > top disk of pole2
else if (pole1TopDisk > pole2TopDisk)
{
push(src, pole1TopDisk);
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When top disk of pole1 < top disk of pole2
else
{
push(dest, pole2TopDisk);
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
}
// Function to show the movement of disks
void moveDisk(char fromPeg, char toPeg, int disk)
{
Console.WriteLine("Move the disk "+disk +
" from "+fromPeg+" to "+toPeg);
}
// Function to implement TOH puzzle
void tohIterative(int num_of_disks, Stack
src, Stack aux, Stack dest)
{
int i, total_num_of_moves;
char s = 'S', d = 'D', a = 'A';
// If number of disks is even, then interchange
// destination pole and auxiliary pole
if (num_of_disks % 2 == 0)
{
char temp = d;
d = a;
a = temp;
}
total_num_of_moves = (int) (Math.Pow(2, num_of_disks) - 1);
// Larger disks will be pushed first
for (i = num_of_disks; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_num_of_moves; i++)
{
if (i % 3 == 1)
moveDisksBetweenTwoPoles(src, dest, s, d);
else if (i % 3 == 2)
moveDisksBetweenTwoPoles(src, aux, s, a);
else if (i % 3 == 0)
moveDisksBetweenTwoPoles(aux, dest, a, d);
}
}
// Driver code
public static void Main(String []args)
{
// Input: number of disks
int num_of_disks = 3;
GFG ob = new GFG();
Stack src, dest, aux;
// Create three stacks of size 'num_of_disks'
// to hold the disks
src = ob.createStack(num_of_disks);
dest = ob.createStack(num_of_disks);
aux = ob.createStack(num_of_disks);
ob.tohIterative(num_of_disks, src, aux, dest);
}
}
// This code is Contributed by Arnab Kundu
Javascript
<script>
// Javascript program for iterative Tower of Hanoi
// A structure to represent a stack
class Stack
{
constructor(capacity) {
this.capacity = capacity;
this.top = -1;
this.array = new Array(capacity);
}
}
// function to create a stack of given capacity.
function createStack(capacity)
{
let stack = new Stack(capacity);
return stack;
}
// Stack is full when top is equal to the last index
function isFull(stack)
{
return (stack.top == (stack.capacity - 1));
}
// Stack is empty when top is equal to -1
function isEmpty(stack)
{
return (stack.top == -1);
}
// Function to add an item to stack.
// It increases top by 1
function push(stack, item)
{
if(isFull(stack))
return;
stack.array[++stack.top] = item;
}
// Function to remove an item from stack.
// It decreases top by 1
function pop(stack)
{
if(isEmpty(stack))
return Number.MIN_VALUE;
return stack.array[stack.top--];
}
// Function to implement legal
// movement between two poles
function moveDisksBetweenTwoPoles(src, dest, s, d)
{
let pole1TopDisk = pop(src);
let pole2TopDisk = pop(dest);
// When pole 1 is empty
if (pole1TopDisk == Number.MIN_VALUE)
{
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When pole2 pole is empty
else if (pole2TopDisk == Number.MIN_VALUE)
{
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
// When top disk of pole1 > top disk of pole2
else if (pole1TopDisk > pole2TopDisk)
{
push(src, pole1TopDisk);
push(src, pole2TopDisk);
moveDisk(d, s, pole2TopDisk);
}
// When top disk of pole1 < top disk of pole2
else
{
push(dest, pole2TopDisk);
push(dest, pole1TopDisk);
moveDisk(s, d, pole1TopDisk);
}
}
// Function to show the movement of disks
function moveDisk(fromPeg, toPeg, disk)
{
document.write("Move the disk "+disk +
" from '"+fromPeg+"' to '"+toPeg + "'</br>");
}
// Function to implement TOH puzzle
function tohIterative(num_of_disks, src, aux, dest)
{
let i, total_num_of_moves;
let s = 'S', d = 'D', a = 'A';
// If number of disks is even, then interchange
// destination pole and auxiliary pole
if (num_of_disks % 2 == 0)
{
let temp = d;
d = a;
a = temp;
}
total_num_of_moves = parseInt(Math.pow(2, num_of_disks) - 1, 10);
// Larger disks will be pushed first
for (i = num_of_disks; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_num_of_moves; i++)
{
if (i % 3 == 1)
moveDisksBetweenTwoPoles(src, dest, s, d);
else if (i % 3 == 2)
moveDisksBetweenTwoPoles(src, aux, s, a);
else if (i % 3 == 0)
moveDisksBetweenTwoPoles(aux, dest, a, d);
}
}
// Input: number of disks
let num_of_disks = 3;
let src, dest, aux;
// Create three stacks of size 'num_of_disks'
// to hold the disks
src = createStack(num_of_disks);
dest = createStack(num_of_disks);
aux = createStack(num_of_disks);
tohIterative(num_of_disks, src, aux, dest);
// This code is contributed by decode2207
</script>
Producción:
Move the disk 1 from 'S' to 'D' Move the disk 2 from 'S' to 'A' Move the disk 1 from 'D' to 'A' Move the disk 3 from 'S' to 'D' Move the disk 1 from 'A' to 'S' Move the disk 2 from 'A' to 'D' Move the disk 1 from 'S' to 'D'
Complejidad de tiempo: O(n)
Espacio Auxiliar: O(n)
Artículos relacionados
Referencias:
http://en.wikipedia.org/wiki/Tower_of_Hanoi#Iterative_solution
Este artículo es una contribución de Anand Barnwal . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA