Trabajo realizado por una fuerza variable

Por lo general, se considera que una persona que baila tiene más energía que una persona sentada. Un guardia de seguridad que ha estado parado en su lugar todo el día ha estado trabajando durante horas. En la vida real, esto parece obvio, pero estos términos y definiciones funcionan de manera diferente cuando se trata de física. En física, el trabajo se ha definido como el producto de la fuerza por el desplazamiento. Esto significa que si no hay desplazamiento, el trabajo realizado es cero, sin importar cuánta fuerza o tiempo se empleó. Esta definición construye conceptos como el teorema trabajo-energía. Veamos esto en detalle.

Trabajar

Considere un bloque de masa M sentado sobre una superficie. Ahora, llega Aman y comienza a aplicar una fuerza F sobre el bloque. Solo aplicando la fuerza durante un tiempo, puede mover el bloque 4 metros en la superficie. El bloque y la fuerza se muestran en la siguiente figura. Ahora, ya que el desplazamiento está ahí. Según la terminología de la física, el trabajo está hecho.

Para una fuerza constante $\vec{F}$ y el desplazamiento $\vec{r}$ . El trabajo realizado se define por,

$W = \vec{F}.\vec{r}$

Este es el producto punto entre dos vectores, por lo que si la Fuerza forma un ángulo $\theta$ con el desplazamiento. Entonces el trabajo realizado estará dado por,

W = |F||r|cos( $\theta$ )

Trabajo realizado por una fuerza variable

Las ecuaciones anteriores son casos de cálculo del trabajo realizado con la suposición de que la fuerza que se aplica al cuerpo es constante. A menudo, este no es el caso. Las fuerzas varían en dirección y magnitud con el tiempo y, a veces, también con la distancia. Entonces, calcular el trabajo realizado con esta suposición no es correcto y no es perfectamente generalizable.

Consideremos una fuerza que cambia su magnitud. Considere el caso de un resorte y la ley de Hooke. Según la ley de Hooke, la fuerza restauradora de un resorte perfectamente elástico es proporcional a su extensión. La dirección de esta fuerza es opuesta a la extensión. Allí la fuerza que actúa está dada por,

F = -kx

Aquí, k es la constante de resorte.

Este es un ejemplo de una Fuerza variable. Para calcular el trabajo realizado por una fuerza variable, debemos sumar todo el trabajo infinitamente pequeño realizado en todos los intervalos infinitesimalmente pequeños. Denotemos el intervalo infinitesimalmente pequeño con “dt”. Entonces, para agregar al trabajo realizado en tal escenario, se debe usar una integral.

El intervalo «dt» se puede usar para calcular el cambio en la extensión del resorte.

dx = vdt

$W = \sum_i F_i\Delta x \\ = \sum_i F_idx \\ = \sum_i F_ivdt$

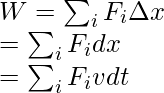
Utilizando las relaciones de fuerza de la ley de Hooke.

$W = \sum_i -kx vdt \\ = \int^{t}_{0} -kxvdt \\ = \int^{x}_{x_0}-kxdx \\ = -\frac{1}{2}k \Delta^2 x$

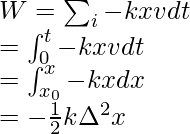
Este trabajo lo realiza una fuerza aplicada sobre el resorte durante una extensión de $\Delta x$

Para una fuerza que es variable y viene dada por $\vec{F}$ y produce un desplazamiento dado por el vector $\vec{dr}$ . El trabajo realizado está dado por,

$W = \int \vec{F}.\vec{dr}$

Gráfica de fuerza-desplazamiento

El concepto anterior se puede entender más claramente usando el gráfico fuerza-desplazamiento. La siguiente gráfica muestra una fuerza variable con el desplazamiento que está produciendo. Se sabe que las integrales representan el área bajo la curva. Entonces, en este caso, el área bajo la curva da el trabajo realizado por la fuerza sobre el cuerpo. El área bajo la curva se divide en muchos rectángulos que representan el $\Delta x$ desplazamiento.

El área de un solo rectángulo es $F.\Delta x$ . Esto representa el trabajo realizado por la fuerza para un desplazamiento infinitesimalmente pequeño. La suma total del área de todos los rectángulos da el trabajo total realizado.

W = $\sum F.\Delta x \\$

⇒ W = ∫Fdx

Problemas de muestra

Pregunta 1: Encuentre el trabajo realizado cuando una fuerza de 20 N que actúa en la dirección del desplazamiento produce un desplazamiento de 5 m.

Solución:

El trabajo realizado por una fuerza constante viene dado por,

W = |F||r|cos( $\theta$ )

Aquí, $\theta = 0$

W = |F||r|cos( $\theta$ )

⇒ W = (20)(5)(cos(0))

⇒ W= 100

Pregunta 2: Encuentra el trabajo realizado cuando una fuerza de F = 30i + 5j produce un desplazamiento r = 5i + 2j.

Solución:

El trabajo realizado por una fuerza constante viene dado por,

W = $\vec{F}.\vec{r}$

$\vec{F} = 30i + 5j$ y $\vec{r} = 5i + 2j$

Cálculo del producto escalar.

W = $\vec{F}.\vec{r}$

⇒ W = (30i + 5j). (5i + 2j)

⇒ W= (30)(5) + (5)(2)

⇒W = 150 + 10

⇒W = 160J

Pregunta 3: Encuentra el trabajo realizado cuando una fuerza de F = x produce un desplazamiento de 4m.

Solución:

El trabajo realizado por una fuerza variable viene dado por,

W = ∫Fdx

F(x) = x

Cálculo del trabajo realizado.

W = $\int^{x}_{0}Fdx \\ = \int^{x}_{0}xdx \\ = [\frac{x^2}{2}]^{x}_{0} \\ = \frac{x^2}{2}$

Aquí, el desplazamiento es x = 4

W = $\frac{x^2}{2}$

⇒ W = $\frac{4^2}{2}$

⇒ W = 8J

Pregunta 4: Encuentra el trabajo realizado cuando una fuerza de F = x ² produce un desplazamiento de 3 m.

Solución:

El trabajo realizado por una fuerza variable viene dado por,

W = ∫Fdx

F(x) = ^x2

Cálculo del trabajo realizado.

W = $\int^{x}_{0}Fdx \\ = \int^{x}_{0}x^2dx \\ = [\frac{x^3}{3}]^{x}_{0} \\ = \frac{x^3}{3}$

Aquí, el desplazamiento es x = 3

W = $\frac{x^3}{3}$

⇒ W = $\frac{3^2}{2}$

⇒ W = 4,5 J

Pregunta 5: Encuentra el trabajo realizado cuando una fuerza de F = x + 4 produce un desplazamiento de 2 m.

Solución:

El trabajo realizado por una fuerza variable viene dado por,

W = ∫Fdx

F(x) = x + 4

Cálculo del trabajo realizado.

W = $\int^{x}_{0}Fdx \\ = \int^{x}_{0}(x + 4)dx \\ = [\frac{x^2}{2} + 4x]^{x}_{0} \\ = \frac{x^2}{2} + 4x$

Aquí, el desplazamiento es x = 2

W = $\frac{x^2}{2} + 4x$

⇒ W = $\frac{2^2}{2} + 4(2)$

⇒ W = 10J

Pregunta 6: Encuentra el trabajo realizado cuando una fuerza de F = sin(x) produce un desplazamiento de -1 a 1.

Solución:

El trabajo realizado por una fuerza variable viene dado por,

W = ∫Fdx

F(x) = sen(x)

Cálculo del trabajo realizado.

W = $\int^{1}_{-1}Fdx \\ = \int^{1}_{-1}sin(x)dx \\ = [-cos(x)]^{1}_{-1} \\ = cos(-1) - cos(1) \\ = 0$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Trabajar

Trabajo realizado por una fuerza variable

Gráfica de fuerza-desplazamiento

Problemas de muestra

Deja una respuesta Cancelar la respuesta