Transformada de Fourier directa e inversa de una imagen en MATLAB

En este artículo, aplicaremos la Transformada de Fourier en imágenes.

Propiedades de la transformada de Fourier:

• Linealidad: La suma de dos funciones correspondientes a la suma de los dos espectros de frecuencia se llama linealidad. Si multiplicamos una función por una constante, la transformada de Fourier de la función resultante se multiplica por la misma constante. La transformada de Fourier de la suma de dos o más funciones es la suma de las transformadas de Fourier de las funciones.
• Escalada:
• Diferenciación:
• Circunvolución:
• Cambio de frecuencia y cambio de tiempo: las coordenadas afectan el cambio de tiempo

La imagen elegida para el experimento de este artículo es la imagen de un camarógrafo famoso.

Figura: Imagen de entrada

Ecuación para DFT: 

Ecuación para IDFT: 

Pasos:

• Lee la imagen.
• Aplicar la transformación de Fourier directa.
• Mostrar imágenes de registro y cambio de FT.

Función utilizada:

• La función incorporada imread() se usa para generar imágenes.
• La función incorporada fft2() se utiliza para aplicar la transformada de Fourier directa en la señal 2D.
• La función incorporada ifft2() se usa para aplicar la transformada inversa de Fourier en la señal 2D.
• La función incorporada fftshift() se usa para cambiar las esquinas al centro en la imagen FT.
• La función incorporada log() se utiliza para evaluar el logaritmo de la señal compleja FT.
• La función incorporada imtool() se usa para mostrar la imagen.

Ejemplo:

% MATLAB code for Forward and 
% Inverse Fourier Transform
  
% FORWARD FOURIER TRANSFORM
k=imread("cameraman.jpg");
  
% Apply fourier transformation.
f=fft2(k);
  
% Take magnitude of FT.
f1=abs(f);
  
% Take log of magnitude of FT.
f2=log(abs(f));
  
% Shift FT from corners to central part.
f3=log(abs(fftshift(f)));
  
% Display all three FT images.
imtool(f1,[]); 
imtool(f2,[]);
imtool(f3,[]);
  
% Remove some frequency from FT.
f(1:20, 20:40)=0;
imtool(log(abs(f)),[]);

Producción:

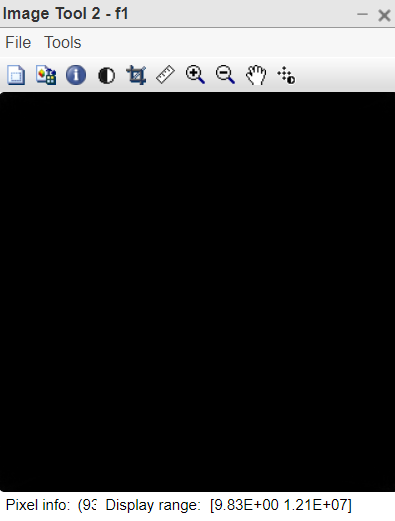
Figura 1: Absoluto de la imagen transformada de Fourier

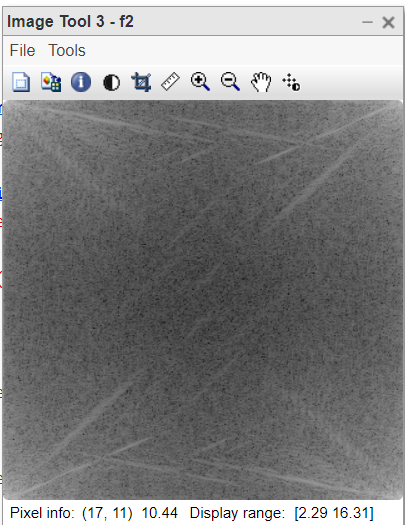
Figura 2: Log del absoluto de FT de imagen

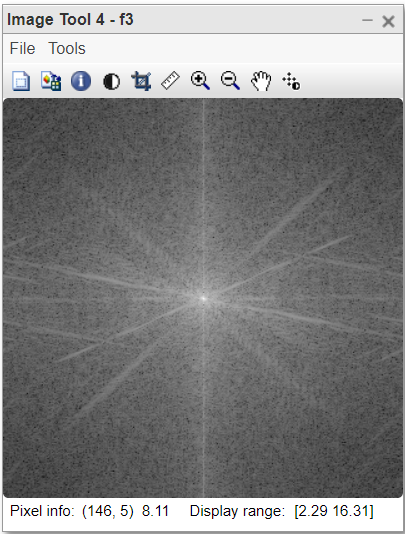
 Figura 3:Espectro centrado de la imagen FT

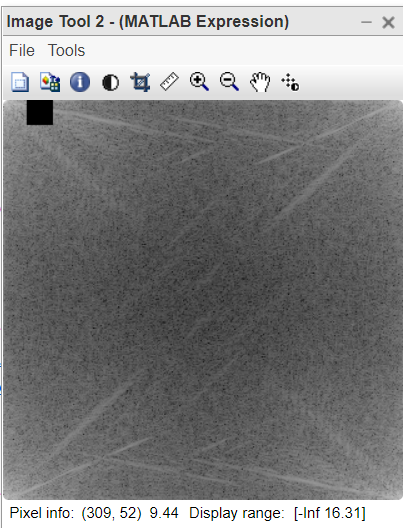
Figura 4: Algunas frecuencias bloqueadas en la imagen FT

Explicación del código:

• k=imread(“camarógrafo.jpg”); Esta línea lee la imagen.
• f=fft2(k); Esta línea calcula la transformación de Fourier.
• f1=abs(f); Esto toma la magnitud de FT.
• f2=log(abs(f)); Esta línea toma el logaritmo de la magnitud de FT.
• f3=log(abs(fftshift(f))); Esta línea desplaza FT de las esquinas a la parte central.
• f(1:20, 20:40)=0; Esta línea elimina frecuencias de FT.

Ejemplo:

% MATLAB code for INVERSE FOURIER TRANSFORM
% apply inverse FT on FTransformed image.
% we get original image in this step.
j=ifft2(f);
  
% Take log of original image.
j1=log(abs(j));
  
% Shift corners to center.
j2=fftshift(j);
  
% Again shift to get original image.
j3=fftshift(j2);
  
% Remove some frequency from FT image.
f(1:20, 20:40)=0;
  
% Apply inverse FT.
j4=ifft2(f);
  
% Display all 4 images.
imtool(j,[]);
imtool(j1,[]); 
imtool(j2,[]);
imtool(j3,[]);%j and j3 are same.
imtool(abs(j4),[]);

Producción:

Figura 1: La imagen de entrada original se obtuvo tomando el FT inverso de la imagen FT

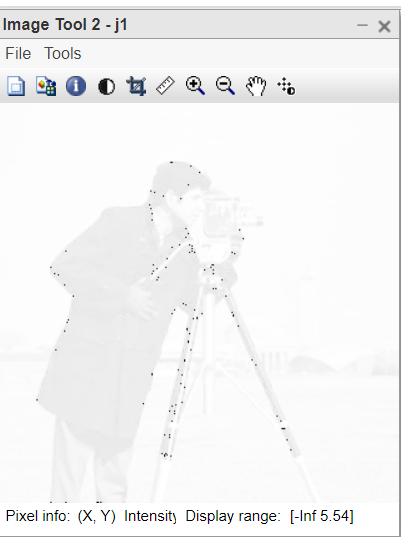
Figura 2: logaritmo de la imagen transformada de Fourier inversa absoluta

Figura 3: Esquinas desplazadas al centro

Figura 4: FT inversa después de eliminar algunas frecuencias del dominio Freq

Explicación del código: 

• j=ifft2(f); Esta línea calcula el FT inverso de la imagen FT.
• f(1:20, 20:40)=0; Esta línea elimina parte de la frecuencia de la imagen FT.
• j4=ifft2(f); Esta línea calcula el FT inverso después de eliminar algunas frecuencias.
• imtool(abs(j4),[]); Esta línea muestra una imagen modificada que contiene algunos artefactos de timbre.

Propiedades:

• No existe una correspondencia biunívoca entre la imagen del camarógrafo y la imagen transformada de Fourier.
• La imagen del camarógrafo representa las intensidades en el dominio espacial.
• La imagen transformada de Fourier representa la frecuencia en el dominio de la frecuencia.
• La frecuencia más baja representa la parte suave de la imagen, mientras que la frecuencia más alta representa los componentes de la forma, como los bordes de una imagen.
• Si la parte de baja frecuencia se elimina de la imagen del dominio de la frecuencia, la imagen del dominio espacial se volverá borrosa.
• Si el valor de frecuencia cualquiera se elimina (se hace 0) en la imagen de dominio de frecuencia, esa frecuencia en particular se eliminará (sustraerá) de cada valor de intensidad en la imagen de dominio espacial.