Durante décadas ha habido una provocación por no poder encontrar la forma más perfecta de calcular la Transformada de Fourier . Allá por el 1800, Gauss ya había formulado sus ideas y, un siglo después, algunos investigadores también, pero la solución estaba en tener que conformarse con las Transformadas Discretas de Fourier . Es una aproximación bastante buena por la cual uno puede estar realmente cerca de representar señales de tiempo continuo y funciona bien (las computadoras y toda la economía lo han estado usando) a pesar de que es finito y no está limitado en el tiempo o en la banda en al mismo tiempo. Además, no tiene en cuenta todas las muestras de la señal. Sin embargo, funciona y es un éxito bastante reconocido.
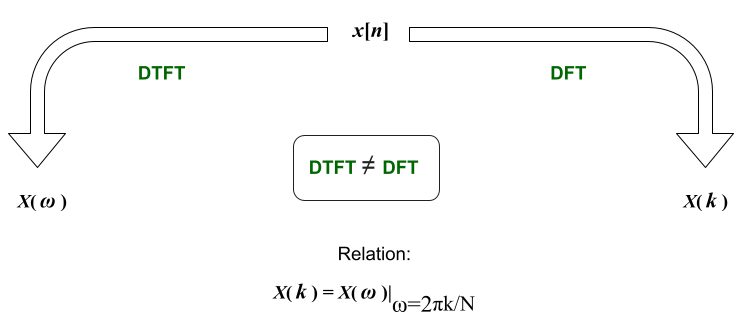
Transformación discreta de Fourier (DFT): comprender las transformadas discretas de Fourier es el objetivo esencial aquí. El Inverso es simplemente un reordenamiento matemático del otro y es bastante simple. La Transformada de Fourier está convirtiendo una función del dominio del tiempo a la frecuencia. Se puede afirmar que las transformadas discretas de Fourier hacen lo mismo, excepto para las señales discretizadas. Sin embargo, no confunda esto con las transformadas de Fourier de tiempo discreto. La diferencia se ha explicado a continuación:
- Las DFT se calculan para secuencias de longitud finita, mientras que las DTFT son para longitudes infinitas. Esta es la razón por la que la suma en DTFT varía de -∞ a +∞.
- Los DTFT se caracterizan por frecuencias de salida que son de naturaleza continua, es decir, ω . Los DFT, por otro lado, dan una salida que tiene frecuencias discretizadas.
- Los DTFT son iguales a los DFT solo para valores muestreados de ω . Esa es la única forma en que derivamos una de la otra.
Las expresiones generales para DFT e IDFT son las siguientes. Tenga en cuenta que los valores integrales de k se toman a partir de 0 y contando hasta N-1. k es simplemente una variable utilizada para referirse al valor muestreado de la función. Sin embargo, dado que IDFT es el inverso de DFT, no se usa k. En su lugar, se utiliza ‘n’. A muchos les resulta confuso cuál es cuál. Tómelo como una actividad libre de estrés para asociar las DFT con una ‘X’ mayúscula y las IDFT con la ‘x’ minúscula.
Ecuación para DFT:
Ecuación para IDFT:
Lo primero que viene a la mente para codificar la expresión anterior es comenzar con una suma. En la práctica, esto se logra ejecutando un bucle e iterando sobre diferentes valores de n (en DFT) yk (en IDFT). Tome nota de cómo uno también debe encontrar diferentes valores de la salida. Cuando k=1, uno puede calcular X[k=1] bastante fácilmente. Sin embargo, en otras aplicaciones, como trazar el espectro de magnitud, también se debe calcular lo mismo para diferentes valores de k. Por lo tanto, se deben introducir dos bucles o un par de bucles anidados.
Otra preocupación más es cómo traducir la segunda mitad de la expresión, que es la constante de Euler elevada a un exponente complejo. Los lectores deben recordar la fórmula que ayuda a describir la constante de Euler elevada a un número complejo en términos de senos y cosenos. Esto es lo siguiente-
Esto nos deja interpretar la segunda mitad del término de suma de la siguiente manera:
Es posible importar bibliotecas (en el caso de C) donde uno podría tener problemas para garantizar la legibilidad del código cuando se trata de escribir esta expresión. Sin embargo, un poco de conocimiento matemático y una conversión simple es el requisito perfecto aquí. Muchos estarían de acuerdo. Tenga en cuenta que esto da lugar a partes imaginarias y reales de la expresión: los términos del coseno son reales y los términos del seno son todos imaginarios. También se puede implementar una perspectiva bastante intuitiva: exprese las secuencias como arrays y use la forma vectorial de DFT e IDFT para los cálculos. Esto se resuelve mejor en MATLAB.
Algoritmo (DFT):
- Inicialice todas las bibliotecas requeridas.
- Pida al usuario que ingrese el número de puntos en la DFT.
- Ahora puede inicializar las arrays y, en consecuencia, solicitar la secuencia de entrada. Esto se debe únicamente a la incapacidad de declarar una array vacía en C. La asignación de memoria dinámica es una de las soluciones. Sin embargo, simplemente reordenar el indicador es una solución justa en sí misma.
- Implemente 2 bucles que calculen el valor de X(k) para un valor específico de k y n. Tenga en cuenta que se usará la fórmula de Euler para sustituir e -j2kπn/N . Esto requiere una división donde calculamos los bits reales e imaginarios de la expresión por separado.
- Muestre el resultado a medida que ejecuta el cálculo.
A continuación se muestra el programa C para implementar el enfoque anterior:
C
// C program for the above approach
#include <math.h>
#include <stdio.h>
// Function to calculate the DFT
void calculateDFT(int len)
{
int xn[len];
float Xr[len];
float Xi[len];
int i, k, n, N = 0;
for (i = 0; i < len; i++) {
printf("Enter the value "
"of x[%d]: ",
i);
scanf("%d", &xn[i]);
}
printf("Enter the number of "
"points in the DFT: ");
scanf("%d", &N);
for (k = 0; k < N; k++) {
Xr[k] = 0;
Xi[k] = 0;
for (n = 0; n < len; n++) {
Xr[k]
= (Xr[k]
+ xn[n] * cos(2 * 3.141592 * k * n / N));
Xi[k]
= (Xi[k]
- xn[n] * sin(2 * 3.141592 * k * n / N));
}
printf("(%f) + j(%f)\n", Xr[k], Xi[k]);
}
}
// Driver Code
int main()
{
int len = 0;
printf("Enter the length of "
"the sequence: ");
scanf("%d4", &len);
calculateDFT(len);
return 0;
}
Aporte:
>> Enter the length of the sequence: 4 >> Enter the value of x[0]: 1 >> Enter the value of x[1]: 4 >> Enter the value of x[2]: 9 >> Enter the value of x[3]: 16 >> Enter the number of points in the DFT: 4
Producción:

Algoritmo (IDFT):
- Inicialice todas las bibliotecas requeridas.
- Pida al usuario que introduzca la duración de la secuencia. Esto se sustituirá como el valor de N. Inicialice los arreglos responsables de almacenar las partes real e imaginaria de la entrada.
- Ahora obtenga las partes real e imaginaria de la secuencia una por una usando un bucle ‘for’ . Recuerde que literalmente estamos invirtiendo el proceso definido para los cálculos de DFT.
- Definir theta. Theta es el exponente al que se eleva e en la conversión de Euler de e iθ , es decir, theta = 2kπn/N.
- Calcula x[n] usando cosenos y senos. Tenga cuidado al usar los signos involucrados en las expresiones.
- Divida la salida obtenida por la longitud o multiplíquela por 1/N e imprima el resultado.
A continuación se muestra el programa C para implementar el enfoque anterior:
C
// C program for the above approach
#include <math.h>
#include <stdio.h>
// Function to calculate the inverse
// discrete fourier transformation
void calculate_IDFT(int len)
{
int x[len];
float Xr[len];
float Xi[len];
int i, k, n, N = 0;
for (i = 0; i < len; i++) {
printf(
"Enter the real and "
"imaginary bits of X(%d): ",
i);
scanf("%f %f", &Xr[i], &Xi[i]);
}
printf("Enter the number of "
"points in the IDFT: ");
scanf("%d", &N);
for (n = 0; n < N; n++) {
x[n] = 0;
for (k = 0; k < N; k++) {
int theta = (2 * 3.141592 * k * n) / N;
x[n] = x[n] + Xr[k] * cos(theta)
+ Xi[k] * sin(theta);
}
x[n] = x[n] / N;
printf("\n x[%d] = %d\n", n,
x[n]);
}
printf("\n-----------x[n]------------\n\n");
}
// Driver Code
int main()
{
int len = 0;
printf("Enter the length of "
"the sequence: ");
scanf("%d", &len);
calculate_IDFT(len);
return 0;
}
Aporte:
>> Enter the length of the sequence: 4 >> Enter the real and imaginary bits of X(0): 30 0 >> Enter the real and imaginary bits of X(1): -8 -11 >> Enter the real and imaginary bits of X(2): -10 0 >> Enter the real and imaginary bits of X(3): -8 12 >> Enter the number of points in the IDFT: 4
La salida de la DFT obtenida anteriormente (no exactamente; espere alguna desviación) se utiliza como entrada para la IDFT.
Producción:

Publicación traducida automáticamente
Artículo escrito por siddhant_baroth y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA