Dado un BST, transfórmelo en un árbol de suma mayor donde cada Node contiene la suma de todos los Nodes mayores que ese Node.
C++
// C++ program to transform a BST to sum tree
#include<iostream>
using namespace std;
// A BST node
struct Node
{
int data;
struct Node *left, *right;
};
// A utility function to create a new Binary Tree Node
struct Node *newNode(int item)
{
struct Node *temp = new Node;
temp->data = item;
temp->left = temp->right = NULL;
return temp;
}
// Recursive function to transform a BST to sum tree.
// This function traverses the tree in reverse inorder so
// that we have visited all greater key nodes of the currently
// visited node
void transformTreeUtil(struct Node *root, int *sum)
{
// Base case
if (root == NULL) return;
// Recur for right subtree
transformTreeUtil(root->right, sum);
// Update sum
*sum = *sum + root->data;
// Store old sum in current node
root->data = *sum - root->data;
// Recur for left subtree
transformTreeUtil(root->left, sum);
}
// A wrapper over transformTreeUtil()
void transformTree(struct Node *root)
{
int sum = 0; // Initialize sum
transformTreeUtil(root, &sum);
}
// A utility function to print indorder traversal of a
// binary tree
void printInorder(struct Node *root)
{
if (root == NULL) return;
printInorder(root->left);
cout << root->data << " ";
printInorder(root->right);
}
// Driver Program to test above functions
int main()
{
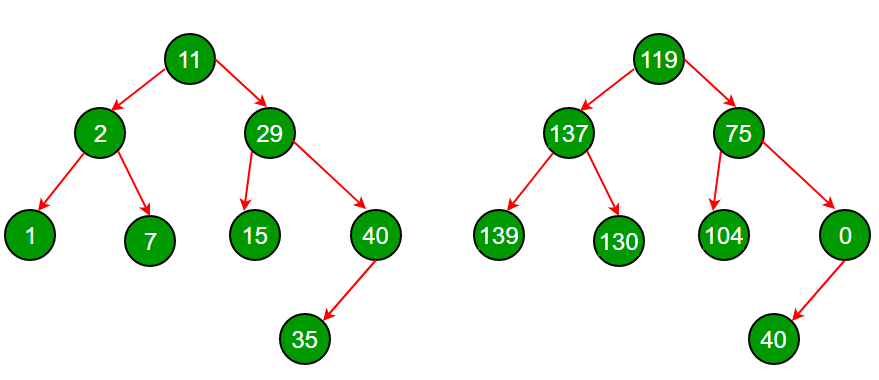
struct Node *root = newNode(11);
root->left = newNode(2);
root->right = newNode(29);
root->left->left = newNode(1);
root->left->right = newNode(7);
root->right->left = newNode(15);
root->right->right = newNode(40);
root->right->right->left = newNode(35);
cout << "Inorder Traversal of given tree\n";
printInorder(root);
transformTree(root);
cout << "\n\nInorder Traversal of transformed tree\n";
printInorder(root);
return 0;
}
Java
// Java program to transform a BST to sum tree
import java.io.*;
class Node
{
int data;
Node left, right;
// A utility function to create a new Binary Tree Node
Node(int item)
{
data = item;
left = right = null;
}
}
class GFG
{
static int sum = 0;
static Node Root;
// Recursive function to transform a BST to sum tree.
// This function traverses the tree in reverse inorder so
// that we have visited all greater key nodes of the currently
// visited node
static void transformTreeUtil(Node root)
{
// Base case
if (root == null)
return;
// Recur for right subtree
transformTreeUtil(root.right);
// Update sum
sum = sum + root.data;
// Store old sum in current node
root.data = sum - root.data;
// Recur for left subtree
transformTreeUtil(root.left);
}
// A wrapper over transformTreeUtil()
static void transformTree(Node root)
{
transformTreeUtil(root);
}
// A utility function to print indorder traversal of a
// binary tree
static void printInorder(Node root)
{
if (root == null)
return;
printInorder(root.left);
System.out.print(root.data + " ");
printInorder(root.right);
}
// Driver Program to test above functions
public static void main (String[] args) {
GFG.Root = new Node(11);
GFG.Root.left = new Node(2);
GFG.Root.right = new Node(29);
GFG.Root.left.left = new Node(1);
GFG.Root.left.right = new Node(7);
GFG.Root.right.left = new Node(15);
GFG.Root.right.right = new Node(40);
GFG.Root.right.right.left = new Node(35);
System.out.println("Inorder Traversal of given tree");
printInorder(Root);
transformTree(Root);
System.out.println("\n\nInorder Traversal of transformed tree");
printInorder(Root);
}
}
// This code is contributed by avanitrachhadiya2155
Python3
# Python3 program to transform a BST to sum tree
class Node:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
# Recursive function to transform a BST to sum tree.
# This function traverses the tree in reverse inorder so
# that we have visited all greater key nodes of the currently
# visited node
def transformTreeUtil(root):
# Base case
if (root == None):
return
# Recur for right subtree
transformTreeUtil(root.right)
# Update sum
global sum
sum = sum + root.data
# Store old sum in current node
root.data = sum - root.data
# Recur for left subtree
transformTreeUtil(root.left)
# A wrapper over transformTreeUtil()
def transformTree(root):
# sum = 0 #Initialize sum
transformTreeUtil(root)
# A utility function to prindorder traversal of a
# binary tree
def printInorder(root):
if (root == None):
return
printInorder(root.left)
print(root.data, end = " ")
printInorder(root.right)
# Driver Program to test above functions
if __name__ == '__main__':
sum=0
root = Node(11)
root.left = Node(2)
root.right = Node(29)
root.left.left = Node(1)
root.left.right = Node(7)
root.right.left = Node(15)
root.right.right = Node(40)
root.right.right.left = Node(35)
print("Inorder Traversal of given tree")
printInorder(root)
transformTree(root)
print("\nInorder Traversal of transformed tree")
printInorder(root)
# This code is contributed by mohit kumar 29
C#
// C# program to transform a BST to sum tree
using System;
public class Node
{
public int data;
public Node left, right;
// A utility function to create a new Binary Tree Node
public Node(int item)
{
data = item;
left = right = null;
}
}
public class GFG{
static int sum = 0;
static Node Root;
// Recursive function to transform a BST to sum tree.
// This function traverses the tree in reverse inorder so
// that we have visited all greater key nodes of the currently
// visited node
static void transformTreeUtil(Node root)
{
// Base case
if (root == null)
return;
// Recur for right subtree
transformTreeUtil(root.right);
// Update sum
sum = sum + root.data;
// Store old sum in current node
root.data = sum - root.data;
// Recur for left subtree
transformTreeUtil(root.left);
}
// A wrapper over transformTreeUtil()
static void transformTree(Node root)
{
transformTreeUtil(root);
}
// A utility function to print indorder traversal of a
// binary tree
static void printInorder(Node root)
{
if (root == null)
return;
printInorder(root.left);
Console.Write(root.data + " ");
printInorder(root.right);
}
// Driver Program to test above functions
static public void Main (){
GFG.Root = new Node(11);
GFG.Root.left = new Node(2);
GFG.Root.right = new Node(29);
GFG.Root.left.left = new Node(1);
GFG.Root.left.right = new Node(7);
GFG.Root.right.left = new Node(15);
GFG.Root.right.right = new Node(40);
GFG.Root.right.right.left = new Node(35);
Console.WriteLine("Inorder Traversal of given tree");
printInorder(Root);
transformTree(Root);
Console.WriteLine("\n\nInorder Traversal of transformed tree");
printInorder(Root);
}
}
// This code is contributed by ab2127
Javascript
<script>
// Javascript program to transform
// a BST to sum tree
// A utility function to create a
// new Binary Tree Node
class Node
{
constructor(item)
{
this.data = item;
this.left=null;
this.right=null;
}
}
let sum = 0;
let Root;
// Recursive function to transform a BST
// to sum tree. This function traverses
// the tree in reverse inorder so that
// we have visited all greater key nodes
// of the currently visited node
function transformTreeUtil(root)
{
// Base case
if (root == null)
return;
// Recur for right subtree
transformTreeUtil(root.right);
// Update sum
sum = sum + root.data;
// Store old sum in current node
root.data = sum - root.data;
// Recur for left subtree
transformTreeUtil(root.left);
}
// A wrapper over transformTreeUtil()
function transformTree(root)
{
transformTreeUtil(root);
}
// A utility function to print indorder
// traversal of a binary tree
function printInorder(root)
{
if (root == null)
return;
printInorder(root.left);
document.write(root.data + " ");
printInorder(root.right);
}
// Driver code
Root = new Node(11);
Root.left = new Node(2);
Root.right = new Node(29);
Root.left.left = new Node(1);
Root.left.right = new Node(7);
Root.right.left = new Node(15);
Root.right.right = new Node(40);
Root.right.right.left = new Node(35);
document.write("Inorder Traversal of given tree<br>");
printInorder(Root);
transformTree(Root);
document.write("<br><br>Inorder Traversal of " +
"transformed tree<br>");
printInorder(Root);
// This code is contributed by unknown2108
</script>
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA