Matplotlib se introdujo teniendo en cuenta, solo el trazado bidimensional. Pero en el momento en que se produjo el lanzamiento de 1.0, las utilidades 3D se desarrollaron sobre la 2D y, por lo tanto, ¡tenemos una implementación de datos 3D disponible hoy! Los gráficos en 3D se habilitan al importar el kit de herramientas mplot3d . Veamos un diagrama de contorno 3d de una función coseno 3d. El código se adjunta como referencia.
| Argumentos de función | Descripción |
|---|---|
| rejilla de malla | Función de numpy utilizada para crear una cuadrícula rectangular a partir de dos arrays unidimensionales dadas que representan la indexación cartesiana o la indexación de Matrix |
| plt.ejes() | Crear objeto del eje |
| hacha.contour3D | Para formar el contorno |
| hacha.set_xlabel | Para etiquetar el eje X |
| hacha.set_title | Para dar un título a la trama |
Ejemplo 1:
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
import math
x = [i for i in range(0, 200, 100)]
y = [i for i in range(0, 200, 100)]
X, Y = np.meshgrid(x, y)
Z = []
for i in x:
t = []
for j in y:
t.append(math.cos(math.sqrt(i*2+j*2)))
Z.append(t)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap=cm.cool)
ax.set_xlabel('a')
ax.set_ylabel('b')
ax.set_zlabel('c')
ax.set_title('3D contour for cosine')
plt.show()
Producción: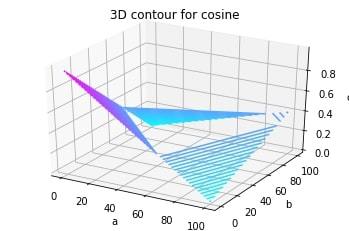
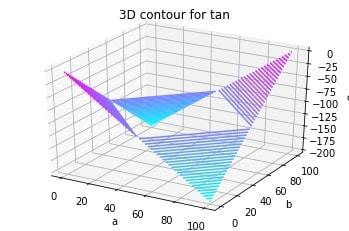
Ejemplo 2: Veamos otro diagrama 3D para una mejor comprensión del concepto. Esta vez, de una función de bronceado 3d.
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
import math
x = [i for i in range(0, 200, 100)]
y = [i for i in range(0, 200, 100)]
X, Y = np.meshgrid(x, y)
Z = []
for i in x:
t = []
for j in y:
t.append(math.tan(math.sqrt(i*2+j*2)))
Z.append(t)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap=cm.cool)
ax.set_xlabel('a')
ax.set_ylabel('b')
ax.set_zlabel('c')
ax.set_title('3D contour for tan')
plt.show()
Producción: