Matplotlib se introdujo teniendo en cuenta, solo el trazado bidimensional. Pero en el momento en que se produjo el lanzamiento de 1.0, las utilidades 3D se desarrollaron sobre la 2D y, por lo tanto, ¡tenemos una implementación de datos 3D disponible hoy! Los gráficos en 3D se habilitan al importar el kit de herramientas mplot3d. En este artículo, nos ocuparemos de los gráficos 3D usando matplotlib.
Ejemplo:
Python3
import numpy as np import matplotlib.pyplot as plt fig = plt.figure() ax = plt.axes(projection ='3d')
Producción:
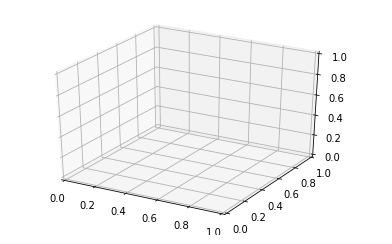
Con la sintaxis anterior, los ejes tridimensionales están habilitados y los datos se pueden trazar en 3 dimensiones. El gráfico de 3 dimensiones brinda un enfoque dinámico y hace que los datos sean más interactivos. Al igual que los gráficos en 2D, podemos usar diferentes formas de representar gráficos en 3D. Podemos hacer un gráfico de dispersión, un gráfico de contorno, un gráfico de superficie, etc. Echemos un vistazo a diferentes gráficos en 3D.
Trazado de líneas y puntos en 3D
Los gráficos con líneas y puntos son los gráficos tridimensionales más simples. ax.plot3d y ax.scatter son la función para trazar gráficos de líneas y puntos respectivamente.
Ejemplo 1: gráfico lineal tridimensional
Python3
# importing mplot3d toolkits, numpy and matplotlib
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
# syntax for 3-D projection
ax = plt.axes(projection ='3d')
# defining all 3 axes
z = np.linspace(0, 1, 100)
x = z * np.sin(25 * z)
y = z * np.cos(25 * z)
# plotting
ax.plot3D(x, y, z, 'green')
ax.set_title('3D line plot geeks for geeks')
plt.show()
Producción:
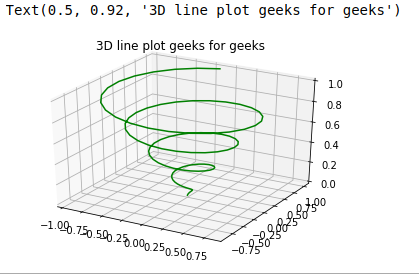
Ejemplo 2: gráfico disperso tridimensional
Python3
# importing mplot3d toolkits
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
# syntax for 3-D projection
ax = plt.axes(projection ='3d')
# defining axes
z = np.linspace(0, 1, 100)
x = z * np.sin(25 * z)
y = z * np.cos(25 * z)
c = x + y
ax.scatter(x, y, z, c = c)
# syntax for plotting
ax.set_title('3d Scatter plot geeks for geeks')
plt.show()
Producción:
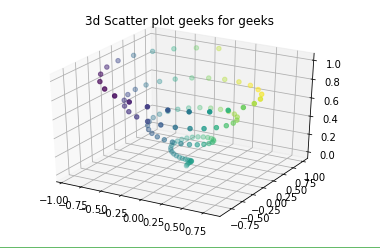
Trazado de gráficos de superficie y estructuras alámbricas
El gráfico de superficie y el gráfico Wireframes funcionan con datos cuadriculados. Toman el valor de la cuadrícula y lo trazan en una superficie tridimensional.
Ejemplo 1: gráfico de superficie
Python3
# importing libraries
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
# defining surface and axes
x = np.outer(np.linspace(-2, 2, 10), np.ones(10))
y = x.copy().T
z = np.cos(x ** 2 + y ** 3)
fig = plt.figure()
# syntax for 3-D plotting
ax = plt.axes(projection ='3d')
# syntax for plotting
ax.plot_surface(x, y, z, cmap ='viridis', edgecolor ='green')
ax.set_title('Surface plot geeks for geeks')
plt.show()
Producción:
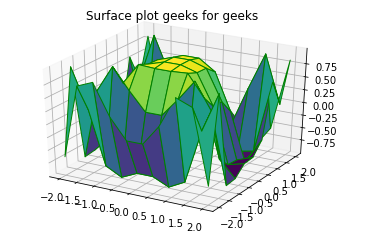
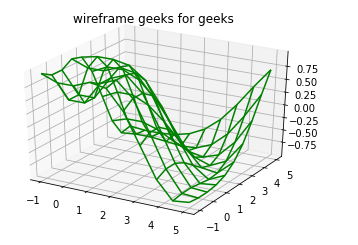
Ejemplo 2: Estructuras alámbricas
Python3
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
# function for z axea
def f(x, y):
return np.sin(np.sqrt(x ** 2 + y ** 2))
# x and y axis
x = np.linspace(-1, 5, 10)
y = np.linspace(-1, 5, 10)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
fig = plt.figure()
ax = plt.axes(projection ='3d')
ax.plot_wireframe(X, Y, Z, color ='green')
ax.set_title('wireframe geeks for geeks');
Producción:
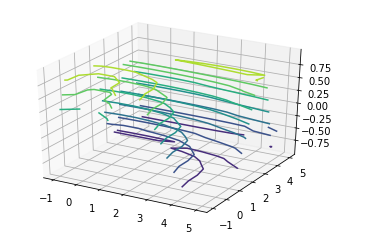
Trazado de gráficos de contorno
El gráfico de contorno toma todos los datos de entrada en cuadrículas regulares bidimensionales y los datos Z se evalúan en cada punto. Usamos la función ax.contour3D para trazar un gráfico de contorno.
Ejemplo:
Python3
from mpl_toolkits import mplot3d import numpy as np import matplotlib.pyplot as plt # function for z axis def f(x, y): return np.sin(np.sqrt(x ** 2 + y ** 3)) # x and y axis x = np.linspace(-1, 5, 10) y = np.linspace(-1, 5, 10) X, Y = np.meshgrid(x, y) Z = f(X, Y) fig = plt.figure() ax = plt.axes(projection ='3d') # ax.contour3D is used plot a contour graph ax.contour3D(X, Y, Z)
Producción:
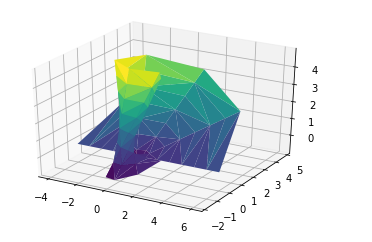
Trazado de triangulaciones de superficie
El gráfico anterior a veces es demasiado restringido e inconveniente. Entonces, con este método, usamos un conjunto de sorteos aleatorios. La función ax.plot_trisurf se usa para dibujar este gráfico. No es tan claro pero más flexible.
Ejemplo:
Python3
from mpl_toolkits import mplot3d import numpy as np import matplotlib.pyplot as plt # angle and radius theta = 2 * np.pi * np.random.random(100) r = 6 * np.random.random(100) # all three axes x = np.ravel(r * np.sin(theta)) y = np.ravel(r * np.cos(theta)) z = f(x, y) ax = plt.axes(projection ='3d') ax.scatter(x, y, z, c = z, cmap ='viridis', linewidth = 0.25); ax = plt.axes(projection ='3d') ax.plot_trisurf(x, y, z, cmap ='viridis', edgecolor ='green');
Producción:
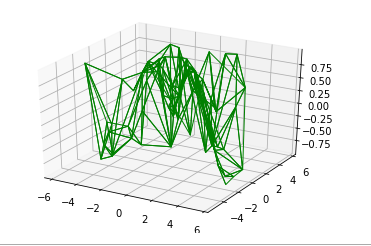
Trazado de la tira de Möbius
La tira de Möbius, también llamada cilindro torcido, es una superficie de un solo lado sin límites. Para crear la tira de Möbius piensa en su parametrización, es una tira bidimensional y necesitamos dos dimensiones intrínsecas. Su ángulo varía de 0 a 2 circular alrededor del bucle y el ancho varía de -1 a 1.
Ejemplo:
Python3
from mpl_toolkits import mplot3d import numpy as np import matplotlib.pyplot as plt from matplotlib.tri import Triangulation theta = np.linspace(0, 2 * np.pi, 10) w = np.linspace(-1, 5, 8) w, theta = np.meshgrid(w, theta) phi = 0.5 * theta # radius in x-y plane r = 1 + w * np.cos(phi) # all three axes x = np.ravel(r * np.cos(theta)) y = np.ravel(r * np.sin(theta)) z = np.ravel(w * np.sin(phi)) # triangulate in the underlying # parameterization tri = Triangulation(np.ravel(w), np.ravel(theta)) ax = plt.axes(projection ='3d') ax.plot_trisurf(x, y, z, triangles = tri.triangles, cmap ='viridis', linewidths = 0.2);
Producción:
Publicación traducida automáticamente
Artículo escrito por _tanya_sri_ y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA