El triángulo trinomio es una variación del triángulo de Pascal . La diferencia entre los dos es que una entrada en el triángulo trinomio es la suma de las tres (en lugar de las dos en el triángulo de Pascal) entradas arriba:

La k -ésima entrada de la n -ésima fila se denota por: ![]()
Las filas se cuentan a partir de 0. Las entradas de la n -ésima fila se indexan comenzando con -n desde la izquierda, y la entrada del medio tiene índice 0. La simetría de las entradas de una fila sobre la entrada del medio se expresa mediante la relación ![]()
Propiedades:
- La n -ésima fila corresponde a los coeficientes en la expansión polinomial de la expansión del trinomio (1 + x + x 2 ) elevado a la n -ésima potencia.
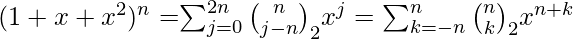
o Simétricamente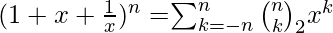
, de ahí el nombre alternativo de coeficientes trinomiales debido a su relación con los coeficientes multinomiales:
- Las diagonales tienen propiedades de intersección, como su relación con los números triangulares .
- La suma de los elementos de la n -ésima fila es 3 n .
Fórmula de recursión
Los coeficientes del trinomio se pueden generar utilizando la siguiente fórmula de recursión: ![]()
![]()
donde, ![]() , para kn
, para kn
Aplicaciones:
- El triángulo corresponde al número de caminos posibles que puede tomar el rey en una partida de ajedrez. La entrada en una celda representa el número de caminos diferentes (utilizando un número mínimo de movimientos) que el rey puede tomar para llegar a la celda.

- El coeficiente de x k en el polinomio (1 + x + x 2 ) n especifica el número de formas diferentes de sacar k cartas al azar de dos juegos de n cartas idénticas. Por ejemplo, en un juego de cartas de este tipo con dos conjuntos de las tres cartas A, B, C, las opciones se ven así:

- Dado un número positivo n . La tarea es imprimir Trinomio Triángulo de altura n.
Ejemplos:
Input : n = 4 Output : 1 1 1 1 1 2 3 2 1 1 3 6 7 6 3 1 Input : n = 5 Output : 1 1 1 1 1 2 3 2 1 1 3 6 7 6 3 1 1 4 10 16 19 16 10 4 1
- A continuación se muestra la implementación de la impresión del triángulo trinomio de altura n:
C++
// CPP Program to print trinomial triangle.
#include<bits/stdc++.h>
using namespace std;
// Function to find the trinomial triangle value.
int TrinomialValue(int n, int k)
{
// base case
if (n == 0 && k == 0)
return 1;
// base case
if(k < -n || k > n)
return 0;
// recursive step.
return TrinomialValue (n - 1, k - 1)
+ TrinomialValue (n - 1, k)
+ TrinomialValue (n - 1, k + 1);
}
// Function to print Trinomial Triangle of height n.
void printTrinomial(int n)
{
// printing n rows.
for (int i = 0; i < n; i++)
{
// printing first half of triangle
for (int j = -i; j <= 0; j++)
cout << TrinomialValue(i, j) << " ";
// printing second half of triangle.
for (int j = 1; j <= i; j++)
cout << TrinomialValue(i, j) << " ";
cout << endl;
}
}
// Driven Program
int main()
{
int n = 4;
printTrinomial(n);
return 0;
}
Java
// Java Program to print trinomial triangle.
import java.util.*;
import java.lang.*;
public class GfG {
// Function to find the trinomial
// triangle value.
public static int TrinomialValue(int n,
int k)
{
// base case
if (n == 0 && k == 0)
return 1;
// base case
if (k < -n || k > n)
return 0;
// recursive step.
return TrinomialValue(n - 1, k - 1)
+ TrinomialValue(n - 1, k)
+ TrinomialValue(n - 1, k + 1);
}
// Function to print Trinomial
// Triangle of height n.
public static void printTrinomial(int n)
{
// printing n rows.
for (int i = 0; i < n; i++)
{
// printing first half of triangle
for (int j = -i; j <= 0; j++)
System.out.print(TrinomialValue(i, j)
+ " ");
// printing second half of triangle.
for (int j = 1; j <= i; j++)
System.out.print(TrinomialValue(i, j)
+ " ");
System.out.println();
}
}
// driver function
public static void main(String argc[])
{
int n = 4;
printTrinomial(n);
}
}
/* This code is contributed by Sagar Shukla */
Python3
# Python3 code to print trinomial triangle.
# Function to find the trinomial triangle value.
def TrinomialValue(n, k):
# base case
if n == 0 and k == 0:
return 1
# base case
if k < -n or k > n:
return 0
# recursive step.
return (TrinomialValue (n - 1, k - 1)+
TrinomialValue (n - 1, k)+
TrinomialValue (n - 1, k + 1))
# Function to print Trinomial Triangle of height n.
def printTrinomial( n ):
# printing n rows.
for i in range(n):
# printing first half of triangle
for j in range(-i, 1):
print(TrinomialValue(i, j),end=" ")
# printing second half of triangle.
for j in range(1, i+1):
print( TrinomialValue(i, j),end=" ")
print("\n",end='')
# Driven Code
n = 4
printTrinomial(n)
# This code is contributed by "Sharad_Bhardwaj".
C#
// C# Program to print trinomial triangle.
using System;
public class GfG {
// Function to find the trinomial
// triangle value.
public static int TrinomialValue(int n,
int k)
{
// base case
if (n == 0 && k == 0)
return 1;
// base case
if (k < -n || k > n)
return 0;
// recursive step.
return TrinomialValue(n - 1, k - 1)
+ TrinomialValue(n - 1, k)
+ TrinomialValue(n - 1, k + 1);
}
// Function to print Trinomial
// Triangle of height n.
public static void printTrinomial(int n)
{
// printing n rows.
for (int i = 0; i < n; i++)
{
// printing first half of triangle
for (int j = -i; j <= 0; j++)
Console.Write(TrinomialValue(i, j)
+ " ");
// printing second half of triangle.
for (int j = 1; j <= i; j++)
Console.Write(TrinomialValue(i, j)
+ " ");
Console.WriteLine();
}
}
// Driver function
public static void Main()
{
int n = 4;
printTrinomial(n);
}
}
/* This code is contributed by Vt_m */
PHP
<?php
// PHP Program to print
// trinomial triangle.
// Function to find the
// trinomial triangle value.
function TrinomialValue($n, $k)
{
// base case
if ($n == 0 && $k == 0)
return 1;
// base case
if($k < -$n || $k > $n)
return 0;
// recursive step.
return TrinomialValue ($n - 1, $k - 1) +
TrinomialValue ($n - 1, $k) +
TrinomialValue ($n - 1, $k + 1);
}
// Function to print Trinomial
// Triangle of height n.
function printTrinomial($n)
{
// printing n rows.
for ($i = 0; $i < $n; $i++)
{
// printing first
// half of triangle
for ($j = -$i; $j <= 0; $j++)
echo TrinomialValue($i, $j), " ";
// printing second
// half of triangle.
for ($j = 1; $j <= $i; $j++)
echo TrinomialValue($i, $j) , " ";
echo "\n";
}
}
// Driver Code
$n = 4;
printTrinomial($n);
// This code is contributed
// by ajit
?>
Javascript
<script>
// JavaScript Program to print trinomial triangle.
// Function to find the trinomial
// triangle value.
function TrinomialValue(n, k)
{
// base case
if (n == 0 && k == 0)
return 1;
// base case
if (k < -n || k > n)
return 0;
// recursive step.
return TrinomialValue(n - 1, k - 1)
+ TrinomialValue(n - 1, k)
+ TrinomialValue(n - 1, k + 1);
}
// Function to print Trinomial
// Triangle of height n.
function printTrinomial(n)
{
// printing n rows.
for (let i = 0; i < n; i++)
{
// printing first half of triangle
for (let j = -i; j <= 0; j++)
document.write(TrinomialValue(i, j)
+ " ");
// printing second half of triangle.
for (let j = 1; j <= i; j++)
document.write(TrinomialValue(i, j)
+ " ");
document.write("<br/>");
}
}
// Driver code
let n = 4;
printTrinomial(n);
// This code is contributed by code_hunt.
</script>
Producción:
1 1 1 1 1 2 3 2 1 1 3 6 7 6 3 1
- A continuación se muestra la implementación de la impresión Trinomial Triangle usando Programación Dinámica y la propiedad del triángulo trinomio, es decir

C++
// C++ Program to print trinomial triangle.
#include <bits/stdc++.h>
#define MAX 10
using namespace std;
// Function to find the trinomial triangle value.
int TrinomialValue(int dp[MAX][MAX], int n, int k)
{
// Using property of trinomial triangle.
if (k < 0)
k = -k;
// If value already calculated, return that.
if (dp[n][k] != 0)
return dp[n][k];
// base case
if (n == 0 && k == 0)
return 1;
// base case
if (k < -n || k > n)
return 0;
// recursive step and storing the value.
return (dp[n][k] = TrinomialValue(dp, n - 1, k - 1)
+ TrinomialValue(dp, n - 1, k)
+ TrinomialValue(dp, n - 1, k + 1));
}
// Function to print Trinomial Triangle of height n.
void printTrinomial(int n)
{
int dp[MAX][MAX] = { 0 };
// printing n rows.
for (int i = 0; i < n; i++) {
// printing first half of triangle
for (int j = -i; j <= 0; j++)
cout << TrinomialValue(dp, i, j) << " ";
// printing second half of triangle.
for (int j = 1; j <= i; j++)
cout << TrinomialValue(dp, i, j) << " ";
cout << endl;
}
}
// Driven Program
int main()
{
int n = 4;
printTrinomial(n);
return 0;
}
// The code is contributed by Gautam goel (gautamgoel962)
C
// CPP Program to print trinomial triangle.
#include<bits/stdc++.h>
#define MAX 10
using namespace std;
// Function to find the trinomial triangle value.
int TrinomialValue(int dp[MAX][MAX], int n, int k)
{
// Using property of trinomial triangle.
if (k < 0)
k = -k;
// If value already calculated, return that.
if (dp[n][k] != 0)
return dp[n][k];
// base case
if (n == 0 && k == 0)
return 1;
// base case
if(k < -n || k > n)
return 0;
// recursive step and storing the value.
return (dp[n][k] = TrinomialValue(dp, n - 1, k - 1)
+ TrinomialValue(dp, n - 1, k)
+ TrinomialValue(dp, n - 1, k + 1));
}
// Function to print Trinomial Triangle of height n.
void printTrinomial(int n)
{
int dp[MAX][MAX] = { 0 };
// printing n rows.
for (int i = 0; i < n; i++)
{
// printing first half of triangle
for (int j = -i; j <= 0; j++)
cout << TrinomialValue(dp, i, j) << " ";
// printing second half of triangle.
for (int j = 1; j <= i; j++)
cout << TrinomialValue(dp, i, j) << " ";
cout << endl;
}
}
// Driven Program
int main()
{
int n = 4;
printTrinomial(n);
return 0;
}
Java
// Java Program to print trinomial triangle.
import java.util.*;
import java.lang.*;
public class GfG {
private static final int MAX = 10;
// Function to find the trinomial triangle value.
public static int TrinomialValue(int dp[][], int n, int k)
{
// Using property of trinomial triangle.
if (k < 0)
k = -k;
// If value already calculated, return that.
if (dp[n][k] != 0)
return dp[n][k];
// base case
if (n == 0 && k == 0)
return 1;
// base case
if (k < -n || k > n)
return 0;
// recursive step and storing the value.
return (dp[n][k] = TrinomialValue(dp, n - 1, k - 1)
+ TrinomialValue(dp, n - 1, k)
+ TrinomialValue(dp, n - 1, k + 1));
}
// Function to print Trinomial Triangle of height n.
public static void printTrinomial(int n)
{
int[][] dp = new int[MAX][MAX];
// printing n rows.
for (int i = 0; i < n; i++) {
// printing first half of triangle
for (int j = -i; j <= 0; j++)
System.out.print(TrinomialValue(dp, i, j) + " ");
// printing second half of triangle.
for (int j = 1; j <= i; j++)
System.out.print(TrinomialValue(dp, i, j) + " ");
System.out.println();
}
}
// driver function
public static void main(String argc[])
{
int n = 4;
printTrinomial(n);
}
}
/* This code is contributed by Sagar Shukla */
Python3
# Python3 code to print trinomial triangle.
# Function to find the trinomial triangle value.
def TrinomialValue(dp , n , k):
# Using property of trinomial triangle.
if k < 0:
k = -k
# If value already calculated, return that.
if dp[n][k] != 0:
return dp[n][k]
# base case
if n == 0 and k == 0:
return 1
# base case
if k < -n or k > n:
return 0
# recursive step and storing the value.
return (TrinomialValue(dp, n - 1, k - 1) +
TrinomialValue(dp, n - 1, k)+
TrinomialValue(dp, n - 1, k + 1))
# Function to print Trinomial Triangle of height n.
def printTrinomial(n):
dp = [[0]*10]*10
# printing n rows.
for i in range(n):
# printing first half of triangle
for j in range(-i,1):
print(TrinomialValue(dp, i, j),end=" ")
# printing second half of triangle.
for j in range(1,i+1):
print(TrinomialValue(dp, i, j),end=" ")
print("\n",end='')
# Driven Program
n = 4
printTrinomial(n)
# This code is contributed by "Sharad_Bhardwaj".
C#
// C# Program to print
// trinomial triangle.
using System;
class GFG
{
private static int MAX = 10;
// Function to find the
// trinomial triangle value.
public static int TrinomialValue(int [,]dp,
int n, int k)
{
// Using property of
// trinomial triangle.
if (k < 0)
k = -k;
// If value already
// calculated, return that.
if (dp[n, k] != 0)
return dp[n, k];
// base case
if (n == 0 && k == 0)
return 1;
// base case
if (k < -n || k > n)
return 0;
// recursive step and storing the value.
return (dp[n, k] = TrinomialValue(dp, n - 1,
k - 1) +
TrinomialValue(dp, n - 1,
k) +
TrinomialValue(dp, n - 1,
k + 1));
}
// Function to print Trinomial
// Triangle of height n.
public static void printTrinomial(int n)
{
int[,] dp = new int[MAX, MAX];
// printing n rows.
for (int i = 0; i < n; i++)
{
// printing first
// half of triangle
for (int j = -i; j <= 0; j++)
Console.Write(TrinomialValue(dp, i,
j) + " ");
// printing second half
// of triangle.
for (int j = 1; j <= i; j++)
Console.Write(TrinomialValue(dp, i,
j) + " ");
Console.WriteLine();
}
}
// Driver Code
static public void Main ()
{
int n = 4;
printTrinomial(n);
}
}
// This code is contributed by ajit
PHP
<?php
// PHP Program to print
// trinomial triangle.
$MAX = 10;
// Function to find the
// trinomial triangle value.
function TrinomialValue($dp, $n, $k)
{
// Using property of
// trinomial triangle.
if ($k < 0)
$k = -$k;
// If value already
// calculated, return that.
if ($dp[$n][$k] != 0)
return $dp[$n][$k];
// base case
if ($n == 0 && $k == 0)
return 1;
// base case
if($k < -$n || $k > $n)
return 0;
// recursive step and
// storing the value.
return ($dp[$n][$k] = TrinomialValue($dp, $n - 1, $k - 1) +
TrinomialValue($dp, $n - 1, $k) +
TrinomialValue($dp, $n - 1, $k + 1));
}
// Function to print Trinomial
// Triangle of height n.
function printTrinomial($n)
{
global $MAX;
$dp;
for ($i = 0; $i < $MAX; $i++)
for ($j = 0; $j < $MAX; $j++)
$dp[$i][$j] = 0;
// printing n rows.
for ($i = 0; $i < $n; $i++)
{
// printing first
// half of triangle
for ($j = -$i; $j <= 0; $j++)
echo TrinomialValue($dp, $i, $j)." ";
// printing second
// half of triangle.
for ($j = 1; $j <= $i; $j++)
echo TrinomialValue($dp, $i, $j)." ";
echo "\n";
}
}
// Driven Code
$n = 4;
printTrinomial($n);
// This code is contributed by mits
?>
Javascript
<script>
// Javascript Program to print trinomial triangle.
var MAX = 10
// Function to find the trinomial triangle value.
function TrinomialValue(dp, n, k)
{
// Using property of trinomial triangle.
if (k < 0)
k = -k;
// If value already calculated, return that.
if (dp[n][k] != 0)
return dp[n][k];
// base case
if (n == 0 && k == 0)
return 1;
// base case
if(k < -n || k > n)
return 0;
// recursive step and storing the value.
return (dp[n][k] = TrinomialValue(dp, n - 1, k - 1)
+ TrinomialValue(dp, n - 1, k)
+ TrinomialValue(dp, n - 1, k + 1));
}
// Function to print Trinomial Triangle of height n.
function printTrinomial(n)
{
var dp = Array.from(Array(MAX), ()=> Array(MAX).fill(0));
// printing n rows.
for (var i = 0; i < n; i++)
{
// printing first half of triangle
for (var j = -i; j <= 0; j++)
document.write( TrinomialValue(dp, i, j) + " ");
// printing second half of triangle.
for (var j = 1; j <= i; j++)
document.write( TrinomialValue(dp, i, j) + " ");
document.write("<br>");
}
}
// Driven Program
var n = 4;
printTrinomial(n);
</script>
Producción:
1 1 1 1 1 2 3 2 1 1 3 6 7 6 3 1