A partir de este tema, por lo general, se hacen preguntas desde alturas y distancias. En ocasiones, se ha observado que, además de alturas y distancias, también se han formulado preguntas directas a partir de razones trigonométricas, como preguntas basadas en cuadrantes, pequeñas preguntas de simplificación, etc. Los conceptos de trigonometría son aplicables si y solo si el triángulo es un triángulo rectángulo.
- π radianes = 180 grados
- sin θ = Perpendicular / Hipotenusa
cos θ = Base / Hipotenusa
tan θ = Perpendicular / Base - En el primer cuadrante, todas las razones trigonométricas (sen, cos, tan, cosec, sec, cot) son positivas.
En el segundo cuadrante, solo sen y cosec son positivos.
En el tercer cuadrante, solo tan y cot son positivos.
En el cuarto cuadrante, solo cos y sec son positivos. - sin 2 θ + cos 2 θ = 1
1 + tan 2 θ = sec 2 θ
1 + cot 2 θ = cosec 2 θ - sin(- θ) = – sin θ
cos(- θ) = cos θ
tan(- θ) = – tan θ
cosec(- θ) = – cosec θ
sec(- θ) = sec θ
cot(- θ) = – cuna - Aquí, θ1 se llama ángulo de elevación y θ2 se llama ángulo de depresión.

- Para un tipo específico de problema de altura y distancias, tenemos una fórmula generalizada. Altura = Distancia recorrida / [cot(ángulo original) – cot(ángulo final)] => h = d / (cot θ1 – cot θ2) Ejemplo: Un hombre estaba parado en un punto a 100 m del edificio. Desde ese punto, el ángulo de elevación de la parte superior del edificio era de 30 grados. Al avanzar 30 m hacia el edificio, el ángulo de elevación cambió a 45 grados. Encuentra la altura del edificio. Solución : Altura = 30 / (cuna 30 – cuna 45) = 30 / ( – 1) = 15 + 15 m

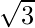
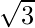
Alturas y Distancias
Los problemas de altura y distancias son simplemente problemas verbales que usan trigonometría.
Problemas de muestra
Pregunta 1 : Simplificar : [ (cos 80) / (sen 10) ] + cos 59 cosec 31
Solución : [ (cos 80) / (sen 10) ] + cos 59 cosec 31 = [ (cos (90 – 10)) / (sen 10) ] + cos 59 cosec (90 – 59)
=> [ (cos 80) / (sen 10) ] + cos 59 cosec 31 = (sen 10 / sen 10) + cos 59 seg 59
=> [ (cos 80) / (sen 10) ] + cos 59 cosec 31 = (sen 10 / sen 10) + cos 59 (1 / cos 59)
=> (sen 10 / sen 10) + cos 59 seg 59 = 1 + 1 = 2
Pregunta 2: Desde lo alto de un faro, los ángulos de depresión de dos barcos son de 30 y 45 grados. Los dos barcos, como se observaba desde lo alto del faro, estaban separados por 100 m. Halla la altura del faro.
Solución: aquí podemos aplicar la fórmula Altura = Distancia / [cot(ángulo original) – cot(ángulo final)]
=> Altura del faro = 100 / (cat 30 – cat 45) = 100 / ( ![]() – 1) = 50
– 1) = 50 ![]() + 50 m
+ 50 m
Pregunta 3 : Una escalera de 80 m de largo está apoyada en una pared. Si la escalera forma un ángulo de 45 grados con el suelo, encuentre la distancia de la escalera a la pared.
Solución: Aquí, cos θ = Base / Hipotenusa => cos 45 = Base / 80 => Base = 80 cos 45 = 80 / = 40 => Distancia de la escalera a la pared = 40 m Pregunta 4: Hay dos postes, uno a cada lado de la carretera. El poste más alto tiene 54 m de altura. Desde la parte superior de este poste, el ángulo de depresión de la parte superior e inferior del poste más corto es de 30 y 60 grados respectivamente. Encuentra la altura del poste más corto. Solución :
![]()
![]()
![]()

Sean AB y CD los dos polos.
Sean AC = xm y CD = hm
Ahora, en el triángulo ABC,
tan 60 = AB / AC
=> ![]() = 54 / AC
= 54 / AC
=> AC = 18 ![]() m
m
Claramente, AC = DE = 18 ![]() m
m
En el triángulo BED,
tan 30 = BE / DE
=> BE = DE tan 30
=> BE = 18 ![]() /
/ ![]() m
m
=> BE = 18 m
=> CD = AE = AB – BE
=> CD = 54 – 18 = 36 m
Por lo tanto, altura del poste más corto = 36 m
Problemas de Trigonometría y Altura y Distancias | Conjunto-2
Este artículo ha sido contribuido por Nishant Arora
Por favor, escriba comentarios si tiene alguna duda relacionada con el tema discutido anteriormente, o si tiene dificultades con alguna pregunta o si le gustaría discutir una pregunta diferente a las mencionadas anteriormente.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA