Trigonometría & Altura y Distancias | Conjunto-2

Pregunta 1: encuentre el valor máximo de (2sinθ + 3 cosθ) 
Solución: valor máximo de (asinθ + bcosθ) = √(a ² + b ² )) 
Entonces, valor máximo = √(2 ² + 3 ² ) 
= √( 4 + 9) 
= √13 

Pregunta 2: Encuentra el valor mínimo de 4tan ² θ + 9cot ² θ 
Solución: Valor mínimo = √ab 
Aquí a = 4 y b = 9 
Valor mínimo = √(4×9) 
= √36 
= 6 

Pregunta 3: Si θ es un ángulo agudo y 7sen ² θ + 3cos ² θ = 4, entonces el valor de tanθ es 
Solución : 7sen ² θ + 3cos ² θ = 4 
7sen ² θ + 3(1-sen ² θ) = 4 
7sen ² θ + 3 – 3sen ² θ = 4 
4sen ² θ = 1 
sen ² θ = 1/4 
senθ = 1/2 
Entonces, θ = 30 ^o 
entonces tanθ = 1/√3 

Pregunta 4:  es igual a 
Solución: Se puede resolver por racionalización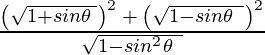 

Use la propiedad:- 
(1-sen ² θ = cos ² θ) 

= 2/cosθ = 2 secθ 

Pregunta 5: Si cosα = a cosβ y senα = b senβ, entonces el valor de sen ² β en términos de a y b es: 
Solución: Elevando al cuadrado ambos lados 
cos ² α = a ² cos ² β 
=> 1 – sen ² α = a ² (1 – sen ² β) ……..(1) 
De nuevo, senα = b senβ 
Al elevar al cuadrado ambos lados 
sen ² α = b ² sen ² β 
Pon el valor de sen ² α en (1) 
1 – b ² sen ² β = a ² – a ² sen ²β) 
a ² – 1 = a ² sen ² β – b ² sen ² β 
a ² – 1 = sen ² β(a ² – b ² ) 
sen ² β = a ² – 1 / (a ^​​2 – b ² ) 

Pregunta 6: El valor de tan1 ^o tan2 ^o tan3 ^o …….tan89 ^o es 
Solución: Arreglar tal que A + B = 90 ^o 
(tan1 ^o tan89 ^o )(tan2 ^o tan88 ^o )…..(tan44 ^o tan46 ^o ) tan45 ^o 
= 1x1x1……1×1 
= 1 

Pregunta 7: Si sen 2A = cos(A – 15 ^o ), donde 2A es un ángulo agudo entonces el valor de A es 
Solución : sen 2A = cos(A – 15 ^o ) 
2A + A – 15 ^o = 90 ^o 
3A = 105o ^A = ^35o 
 

Pregunta 8: 
entonces el valor de senθ es 
Solución : Por componendo y dividendo 
tanθ/cotθ = 3/1 
=> sen ² θ = 3cos ² θ 
=> sen ² θ = 3(1 – sen ² θ) 
=> 4 sen ² θ = 3 
=> sen ² θ = 3/4 
sen θ = √/2 

Pregunta 9: Si tan (π/2 – θ/2) = √3 entonces el valor de cosθ es 
Solución : tan (π/2 – θ/2) = √3 
=> tan (90 – θ/2) = √ 3 
=> cotθ/2 = √3 = cot 30 ^o 
=> θ/2 = 30 ^o 
=> θ = 60 ^o 
entonces cosθ = cos60 ^o = 1/2 

Pregunta 10: a, b, c son las longitudes de tres lados de un triángulo ABC. Si a, b, c están relacionados por la relación a ² + b ² + c ² = ab + bc + ca, entonces el valor de (sin ² A + sin ² B + sin ² C) es 
Solución: Acc. interrogar 
a ² + b ² + c ² – ab – bc – ca = 0 
=>2a ² + 2b ² + 2c ² – 2ab – 2bc – 2ca = 0 
=>(ab) ² + (bc) ² + (ca ) ² = 0 
=> a=b=c 
Los tres lados son iguales, entonces es un triángulo equilátero. 
entonces ∠A = ∠B = ∠C = 60 ² 
Entonces, sen ² 60 + sen ² 60 + sen ² 60 
= 3(√3/2) ² 
= 9/4 

Pregunta 11: El ángulo de elevación de un avión desde un punto en el suelo es de 30 ^o . Después de volar durante 30 segundos, la elevación cambia a 60 ^o . Si el avión vuela a una altura de 4500 metros, entonces la velocidad del avión en km/h es 
Solución: 
 

En ∆ABE 
tan 60 = P/B = 4500/AB 
√3 = 4500/AB 
AB = 4500/√3 

En ∆ACD 
tan 30 = 4500/AC 
1/√3= 4500/AC 
AC = 4500√3 

Distancia recorrida por el avión en 30 segundos = AC – AB 
=4500√3 – 4500/√3 
= (13500 – 4500)/√3 
= 9000/√3 
= 3000√3 

Velocidad = Distancia/tiempo = 3000√3 / 30 
= 100√3 x 18/5 (para obtener km/hr) 
= 360√3 
Por lo tanto, la velocidad del avión es 360√3 km/hr . 

Pregunta 12: Hay dos torres, una a cada lado de la carretera, justo una frente a la otra. Una torre tiene 54 m de altura. Desde la parte superior de esta torre, los ángulos de la depresión de la parte superior y el pie de la otra torre son 30 y 60 respectivamente. La altura de la otra torre es: 
Solución: 
 

AB y CD son Torres. 
BD es el ancho de la carretera. 
AB = 54 m 
In ∆ AEC 
tan 30 = AE/EC = 1/√3 
=> AE : EC = 1 : √3 
In ∆ABD 
tan 60 = AB/BD 
√3 = AB/BD 
=> AB : BD = √ 3 : 1 
Del diagrama sabemos EB = CD y EC = BD 
Ahora, 

AB     :     BD     :     AE
             √3           1
√3     :      1
3      :     √3     :     1

CD = AB – AE = 3 – 1 = 2 unidades 

3 unidades de AB -> 54 m 
1 unidad -> 18 
Luego 2 unidades -> 36 m 
Por lo tanto, la altura de la otra torre es de 36 m .