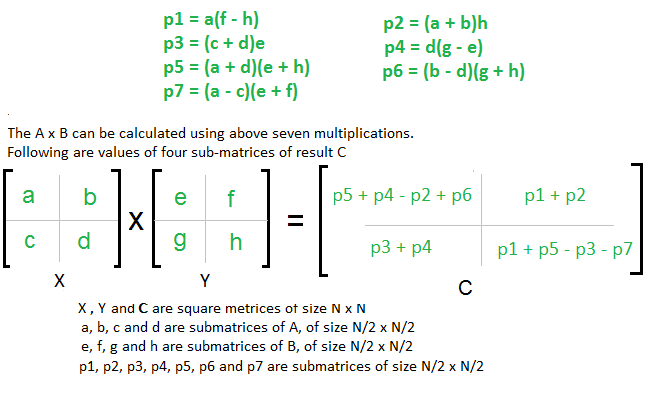
La array de Strassen es un método Divide and Conquer que nos ayuda a multiplicar dos arrays (de tamaño n X n).
Puede consultar el enlace, para tener el conocimiento sobre Matrix de Strassen primero: divide y vencerás | Conjunto 5 (Multiplicación de arrays de Strassen) Pero este método necesita incluir algunas ecuaciones, así que te diré la forma más sencilla de recordarlas:
Solo necesitas recordar 4 Reglas:
- AHED (Aprenderlo como ‘Adelante’)
- Diagonal
- Última RC
- Primera RC
Además, considere X como (Fila +) e Y como (Columna -) array Siga los pasos:
- Escriba P1 = A; P2 = H; P3 = E; P4 = D
- Para P5 usaremos la regla diagonal, es decir (suma de los elementos diagonales de la array X) * (suma de los elementos diagonales de la array Y), obtenemos P5 = (A + D)* (E + H)
- Para P6 usaremos la última regla CR, es decir, la última columna de X y la última fila de Y, y recordaremos que Fila+ y Columna-, es decir, (B – D) * (G + H), obtenemos P6 = (B – D) * ( G + H)
- Para P7 usaremos la primera regla CR, es decir, la primera columna de X y la primera fila de Y, y recordaremos que Fila+ y Columna-, es decir, (A – C) * (E + F), obtenemos P7 = (A – C) * ( E + F)
- Vuelva a P1: tenemos A allí y su elemento adyacente en Y Matrix es E, ya que Y es Column Matrix, por lo que seleccionamos una columna en Y tal que E no venga, encontramos FH Column, entonces multiplique A con (F – H) Entonces, finalmente P1 = A * (F – H)
- Regrese a P2: tenemos H allí y su elemento adyacente en X Matrix es D, ya que X es Row Matrix, por lo que seleccionamos una Fila en X tal que D no vendrá, encontramos la Columna AB, entonces multiplique H con (A + B) Entonces, finalmente P2 = (A + B) * H
- Regrese a P3: tenemos E allí y su elemento adyacente en X Matrix es A, ya que X es Row Matrix, por lo que seleccionamos una Fila en X tal que A no vendrá, encontramos la Columna CD, entonces multiplique E con (C+ D) Entonces, finalmente P3 = (C+ D) * E
- Regrese a P4: tenemos D allí y su elemento adyacente en Y Matrix es H, ya que Y es Column Matrix, por lo que seleccionamos una columna en Y tal que H no venga, encontramos la columna GE, así que multiplique D con (G – E) Entonces, finalmente P4 = D * (G – E)
- Recuerde contar: escriba P1 + P2 en C2
- Escriba P3 + P4 en su posición diagonal, es decir, en C3
- Escriba P4 + P5 + P6 en la primera posición y reste P2, es decir, C1 = P4 + P5 + P6 – P2
- Escriba los valores impares en la última posición con signos alternantes – y +, es decir, P1 P3 P5 P7 se convierte en C4 = P1 – P3 + P5 – P7
Implementación:
C++
#include <bits/stdc++.h>
#include <cmath>
#define vi vector<int>
#define vii vector<vi>
using namespace std;
/* finding next square of 2*/
int nextPowerOf2(int k)
{
return pow(2, int(ceil(log2(k))));
}
// printing matrix
void display(vii C, int m, int n)
{
for (int i = 0; i < m; i++)
{
cout << "|"
<< " ";
for (int j = 0; j < n; j++)
{
cout << C[i][j] << " ";
}
cout << "|" << endl;
}
}
//! addition and subtraction
void add(vii &A, vii &B, vii &C, int size)
{
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
C[i][j] = A[i][j] + B[i][j];
}
}
}
void sub(vii &A, vii &B, vii &C, int size)
{
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
C[i][j] = A[i][j] - B[i][j];
}
}
}
//!-----------------------------
void Strassen_algorithm(vii &A, vii &B, vii &C, int size)
{
if (size == 1)
{
C[0][0] = A[0][0] * B[0][0];
return;
}
else
{
int newSize = size / 2;
vi z(newSize);
vii a(newSize, z), b(newSize, z), c(newSize, z), d(newSize, z),
e(newSize, z), f(newSize, z), g(newSize, z), h(newSize, z),
c11(newSize, z), c12(newSize, z), c21(newSize, z), c22(newSize, z),
p1(newSize, z), p2(newSize, z), p3(newSize, z), p4(newSize, z),
p5(newSize, z), p6(newSize, z), p7(newSize, z), fResult(newSize, z),
sResult(newSize, z);
int i, j;
//! divide the matrix in equal parts
for (i = 0; i < newSize; i++)
{
for (j = 0; j < newSize; j++)
{
a[i][j] = A[i][j];
b[i][j] = A[i][j + newSize];
c[i][j] = A[i + newSize][j];
d[i][j] = A[i + newSize][j + newSize];
e[i][j] = B[i][j];
f[i][j] = B[i][j + newSize];
g[i][j] = B[i + newSize][j];
h[i][j] = B[i + newSize][j + newSize];
}
}
/*
A B C
[a b] * [e f] = [c11 c12]
[g h] [c21 c22]
p1,p2,p3,p4=AHED for this: A:Row(+) and B:Column(-)
p5=Diagonal :both +ve
p6=Last CR :A:Row(-) B:Column(+)
p7=First CR :A:Row(-) B:Column(+)
*/
//! calculating all strassen formulas
//*p1=a*(f-h)
sub(f, h, sResult, newSize);
Strassen_algorithm(a, sResult, p1, newSize);
//*p2=h*(a+b)
add(a, b, fResult, newSize);
Strassen_algorithm(fResult, h, p2, newSize);
//*p3=e*(c+d)
add(c, d, fResult, newSize);
Strassen_algorithm(fResult, e, p3, newSize);
//*p4=d*(g-e)
sub(g, e, sResult, newSize);
Strassen_algorithm(d, sResult, p4, newSize);
//*p5=(a+d)*(e+h)
add(a, d, fResult, newSize);
add(e, h, sResult, newSize);
Strassen_algorithm(fResult, sResult, p5, newSize);
//*p6=(b-d)*(g+h)
sub(b, d, fResult, newSize);
add(g, h, sResult, newSize);
Strassen_algorithm(fResult, sResult, p6, newSize);
//*p7=(a-c)*(e+f)
sub(a, c, fResult, newSize);
add(e, f, sResult, newSize);
Strassen_algorithm(fResult, sResult, p7, newSize);
/* calculating all elements of C by p1,p2,p3
c11=p4+p5+p6-p2
c12=p1+p2
c21=p3+p4
c22=p1-p3+p5-p7
*/
add(p1, p2, c12, newSize); //!
add(p3, p4, c21, newSize); //!
add(p4, p5, fResult, newSize);
add(fResult, p6, sResult, newSize);
sub(sResult, p2, c11, newSize); //!
sub(p1, p3, fResult, newSize);
add(fResult, p5, sResult, newSize);
sub(sResult, p7, c22, newSize); //!
// Grouping the results obtained in a single matrix:
for (i = 0; i < newSize; i++)
{
for (j = 0; j < newSize; j++)
{
C[i][j] = c11[i][j];
C[i][j + newSize] = c12[i][j];
C[i + newSize][j] = c21[i][j];
C[i + newSize][j + newSize] = c22[i][j];
}
}
}
}
/*for converting matrix to square matrix*/
void ConvertToSquareMat(vii &A, vii &B, int r1, int c1, int r2, int c2)
{
int maxSize = max({r1, c1, r2, c2});
int size = nextPowerOf2(maxSize);
vi z(size);
vii Aa(size, z), Bb(size, z), Cc(size, z);
for (unsigned int i = 0; i < r1; i++)
{
for (unsigned int j = 0; j < c1; j++)
{
Aa[i][j] = A[i][j];
}
}
for (unsigned int i = 0; i < r2; i++)
{
for (unsigned int j = 0; j < c2; j++)
{
Bb[i][j] = B[i][j];
}
}
Strassen_algorithm(Aa, Bb, Cc, size);
vi temp1(c2);
vii C(r1, temp1);
for (unsigned int i = 0; i < r1; i++)
{
for (unsigned int j = 0; j < c2; j++)
{
C[i][j] = Cc[i][j];
}
}
display(C, r1, c1);
}
int main()
{
vii a = {
{1, 2, 3},
{1, 2, 3},
{0, 0, 2}};
vii b = {
{1, 0, 0},
{0, 1, 0},
{0, 0, 1}};
ConvertToSquareMat(a, b, 3, 3, 3, 3); // A[][],B[][],R1,C1,R2,C2
return 0;
}
| 1 2 3 | | 1 2 3 | | 0 0 2 |
Este artículo es una contribución de . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA