Uso compartido de secretos aditivos y proactivación de acciones: uso de Python

Un esquema de intercambio de secretos es un esquema criptográfico que implica la división de un valor secreto en múltiples fragmentos/acciones de una manera que evita que un único accionista tenga un conocimiento completo del secreto original. Por lo tanto, el secreto se divide en múltiples acciones y se distribuye entre múltiples participantes. Por lo tanto, el control sobre el valor secreto se distribuye y no está en manos de una sola parte. 
El ejemplo más simple de un esquema de intercambio de secretos es el intercambio de secretos aditivosque implica dividir un secreto numérico en fragmentos que se suman al secreto original. Una vez dividida en acciones, cada acción se distribuye a diferentes participantes. Ninguno de los participantes individuales tiene suficiente información para reconstruir el secreto. Para reconstruir el secreto, todos los participantes deben juntar sus acciones para revelar el valor del secreto original.
 

Fig. 1: División de un secreto entre tres partes mediante el uso compartido de aditivos

Ejemplo 
Suponga que existen las siguientes condiciones: 
 

• El secreto que queremos dividir viene dado por el valor s = 12345
• El número de participantes en el sistema es n = 3 . Por lo tanto, necesitamos obtener tres acciones, una para cada parte.
• Cuando todas las partes se juntan y combinan sus acciones, se revela el secreto.

Una división arbitraria del secreto podría ser:  . Por lo tanto, la primera parte recibe una acción con un valor de 3512, la segunda parte recibe 2100 y la tercera recibe 6733. Claramente, a menos que las tres partes reúnan sus acciones, el secreto no puede ser revelado. Este esquema se denomina esquema de compartición n-out-of-n, ya que todas las acciones son necesarias para la reconstrucción secreta.
 

Uso compartido aditivo sobre un campo finito

Convencionalmente, los valores secretos y los valores compartidos están vinculados a un campo finito donde se realizan todos los cálculos. Todas las acciones excepto las últimas, en tal esquema, se eligen al azar, asegurando que pertenecen al campo finito elegido. Suponga que (n-1) del total de n acciones son S(1), S(2), …, S(n-1) . La parte final se calcula como S(n) = V – (S(1) + S(2) + … + S(n-1)) donde V es el valor del secreto original.
Para recapitular, elegimos (n-1) participaciones aleatorias y calculamos la participación final. 
 

import random
 
def getAdditiveShares(secret, N, fieldSize):
    '''Generate N additive shares from 'secret' in finite field of size 'fieldSize'.'''
 
    # Generate n-1 shares randomly
    shares = [random.randrange(fieldSize) for i in range(N-1)]
 
    # Append final share by subtracting all shares from secret
    # Modulo is done with fieldSize to ensure share is within finite field
    shares.append((secret - sum(shares)) % fieldSize )
    return shares
 
def reconstructSecret(shares, fieldSize):
    '''Regenerate secret from additive shares'''
    return sum(shares) % fieldSize
 
if __name__ == "__main__":
    # Generating the shares
    shares = getAdditiveShares(1234, 5, 10**5)
    print('Shares are:', shares)
     
    # Reconstructing the secret from shares
    print('Reconstructed secret:', reconstructSecret(shares, 10**5))

Shares are: [488, 62586, 9652, 49515, 78993]
Reconstructed secret: 1234

Proactivación de Acciones Aditivas

La proactivación se refiere a la actualización de los recursos compartidos después de intervalos fijos para reducir la posibilidad de que un atacante acceda al secreto. Se supone que un atacante puede obtener acceso a las acciones en poder de cualquier participante en un tiempo razonable. Sin embargo, el compromiso de una sola acción no revela todo el secreto. Como tal, el atacante tendrá que comprometer todos los recursos compartidos generados para obtener acceso al secreto real. Aquí es donde entra en juego la Proactivación. Con la proactivación, todos los recursos compartidos se actualizan arbitrariamente después de un intervalo fijo, de modo que es posible que el atacante nunca tenga acceso a todos los recursos compartidos más actuales. Por lo tanto, si los recursos compartidos se actualizan a una velocidad tal que el adversario solo tiene acceso a un subconjunto de todos los recursos compartidos en un momento dado, el esquema está protegido contra compromisos.
El objetivo con Proactivation es mantener el mismo valor clave pero cambiar su representación de acciones. Se genera un nuevo conjunto de recursos compartidos adicionales después de cada ciclo de vida de la siguiente manera: 
 

1. Cada parte aditiva S(i) se subdivide en subfragmentos d(i, 1), d(i, 2), …, d(i, n) de modo que la suma de todos los d(i, j) da como resultado S(i ) y n es el número de participantes en el sistema 
    
2. El subfragmento d(i, j) es distribuido por la parte propietaria, “ i ” , a la parte “ j ” . De esta manera, todos los participantes intercambian sus subfragmentos.
3. Para calcular su parte actualizada, party i agrega los subfragmentos que recibió de todos los demás participantes de la siguiente manera: 

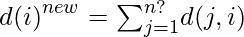
En una observación más cercana, vemos que cada accionista esencialmente realiza una distribución aditiva de sus propias acciones y distribuye las subacciones generadas entre los participantes. Posteriormente, cada participante suma las subacciones recibidas. De esta manera, el secreto original se conserva mientras se actualizan las acciones en poder de los participantes. 
 

Fig. 02: los recursos compartidos adicionales se actualizan en Proactivation sin alterar el secreto en sí

# Additive Sharing with facility to Refresh shares via Proactivization
import random
 
def getAdditiveShares(secret, N, fieldSize):
    '''Generate N additive shares from 'secret' in finite field of size 'fieldSize'.'''
 
    # Generate n-1 shares randomly
    shares = [random.randrange(fieldSize) for i in range(N-1)]
    # Append final share by subtracting all shares from secret
    shares.append((secret - sum(shares)) % fieldSize )
    return shares
 
def reconstructSecret(shares, fieldSize):
    '''Regenerate secret from additive shares'''
    return sum(shares) % fieldSize
 
def proactivizeShares(shares):
    '''Refreshed shares by proactivization'''
     
    n = len(shares)
    refreshedShares = [0]*n
 
    for s in shares:
 
        # Divide each share into sub-fragments using additive sharing
        subShares = getAdditiveShares(s, n, 10**5)
 
        # Add subfragments of corresponding parties
        for p, sub in enumerate(subShares):
            refreshedShares[p] += sub
             
    return refreshedShares
 
if __name__ == "__main__":
    # Generating the shares
    shares = getAdditiveShares(1234, 5, 10**5)
    print('Shares are:', shares)
 
    # Running Proactivization
    newShares = proactivizeShares(shares)
    print('Refreshed Shares are:', newShares)
     
    # Reconstructing secret from refreshed shares
    print('Secret:', reconstructSecret(newShares, 10**5))

Shares are: [45142, 41833, 39277, 49009, 25973]
Refreshed Shares are: [298371, 255404, 117787, 239851, 189821]
Secret: 1234