Variabilidad en la programación R

La variabilidad (también conocida como dispersión estadística ) es otra característica de las estadísticas descriptivas. Las medidas de tendencia central y la variabilidad juntas forman parte de las estadísticas descriptivas. La variabilidad muestra la dispersión de un conjunto de datos alrededor de un punto.

Ejemplo: supongamos que existen 2 conjuntos de datos con el mismo valor medio:

A = 4, 4, 5, 6, 6
Media(A) = 5

B = 1, 1, 5, 9, 9
Media(B) = 5

Entonces, para diferenciar entre los dos conjuntos de datos, R ofrece varias medidas de variabilidad.

Medidas de Variabilidad

Las siguientes son algunas de las medidas de variabilidad que ofrece R para diferenciar entre conjuntos de datos:

Diferencia
Desviación Estándar
Rango
Desviación media
Rango intercuartil

Diferencia

La varianza es una medida que muestra qué tan lejos está cada valor de un punto en particular, preferiblemente el valor medio. Matemáticamente, se define como el promedio de las diferencias al cuadrado del valor medio.

Fórmula:

$\displaystyle \sigma^2 = \frac{\displaystyle\sum_{i=1}^{n}(x_i - \mu)^2} {n}$

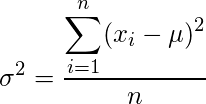
dónde,

$\sigma^2$ especifica la varianza del conjunto de datos
$x_i$ especifica el $i^{\text{th}}$ valor en el conjunto de datos
$\mu$ especifica la media del conjunto de datos
n especifica el número total de observaciones

En el lenguaje R, hay una función integrada estándar para calcular la varianza de un conjunto de datos.

Sintaxis: var(x)

Parámetro:
x: Es vector de datos

Ejemplo:

# Defining vector
x <- c(5, 5, 8, 12, 15, 16)
  
# Print variance of x
print(var(x))

Producción:

[1] 23.76667

Desviación Estándar

La desviación estándar en las estadísticas mide la dispersión de los valores de los datos con respecto a la media y, matemáticamente, se calcula como la raíz cuadrada de la varianza.

Fórmula: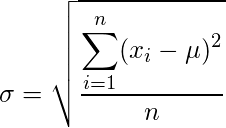
$\displaystyle \sigma = \sqrt{\frac{\displaystyle\sum_{i=1}^{n}(x_i - \mu)^2} {n}}$

dónde,

$\sigma$ especifica la desviación estándar del conjunto de datos
$x_i$ especifica el $i^{\text{th}}$ valor en el conjunto de datos
$\mu$ especifica la media del conjunto de datos
n especifica el número total de observaciones

En el lenguaje R, no hay una función integrada estándar para calcular la desviación estándar de un conjunto de datos. Entonces, modificando el código para encontrar la desviación estándar del conjunto de datos.

Ejemplo:

# Defining vector
x <- c(5, 5, 8, 12, 15, 16)
  
# Standard deviation
d <- sqrt(var(x))
  
# Print standard deviation of x
print(d)

Producción:

[1] 4.875107

Rango

El rango es la diferencia entre el valor máximo y mínimo de un conjunto de datos. En lenguaje R, max()y min()se usa para encontrar lo mismo, a diferencia de range()la función que devuelve el valor mínimo y máximo del conjunto de datos.

Ejemplo:

# Defining vector
x <- c(5, 5, 8, 12, 15, 16)
  
# range() function output
print(range(x))
  
# Using max() and min() function
# to calculate the range of data set
print(max(x)-min(x))

Producción:

[1]  5 16
[1] 11

Desviación media

La desviación media es una medida calculada tomando un promedio de la media aritmética de la diferencia absoluta de cada valor del valor central. El valor central puede ser la media, la mediana o la moda.

Fórmula: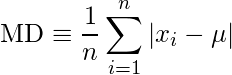
$\displaystyle \mathrm{MD} \equiv \frac{1}{n} \sum_{i=1}^{n}\left|x_{i}-\mu\right|$

dónde,

$x_i$ especifica el $i^{\text{th}}$ valor en el conjunto de datos
$\mu$ especifica la media del conjunto de datos
n especifica el número total de observaciones

En lenguaje R, no existe una función integrada estándar para calcular la desviación media. Entonces, modificando el código para encontrar la desviación media del conjunto de datos.

Ejemplo:

# Defining vector
x <- c(5, 5, 8, 12, 15, 16)
  
# Mean deviation
md <- sum(abs(x-mean(x)))/length(x)
  
# Print mean deviation
print(md)

Producción:

[1] 4.166667

Rango intercuartil

El rango intercuartil se basa en dividir un conjunto de datos en partes llamadas cuartiles. Hay 3 valores de cuartil (Q1, Q2, Q3) que dividen todo el conjunto de datos en 4 partes iguales. Q2 especifica la mediana de todo el conjunto de datos.

Matemáticamente, el rango intercuartil se representa como:

RIC = Q3 – Q1

dónde,

Q3 especifica la mediana de los n valores más grandes
Q1 especifica la mediana de los n valores más pequeños

En el lenguaje R, hay una función integrada para calcular el rango intercuartílico del conjunto de datos.

Sintaxis: IQR(x)

Parámetro:
x: Especifica el conjunto de datos

Ejemplo:

# Defining vector
x <- c(5, 5, 8, 12, 15, 16)
  
# Print Interquartile range
print(IQR(x))

Producción:

[1] 8.5

Publicación traducida automáticamente

Artículo escrito por utkarsh_kumar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Medidas de Variabilidad

Diferencia

Desviación Estándar

Rango

Desviación media

Rango intercuartil

Deja una respuesta Cancelar la respuesta