Velocidad de una onda viajera

En general, casi todos los materiales y objetos en la tierra tienen fuerzas de unión elásticas. Cuando el cuerpo se comprime o se libera, estas fuerzas elásticas comienzan a actuar y el movimiento de una parte del sistema afecta a otras partes. Por lo tanto, el movimiento de una parte del sistema también afecta a las otras partes del sistema, creando así una perturbación que viaja a través de todo el sistema en forma de onda. Por ejemplo, cada vez que se arrojan guijarros al agua, se generan ondas que viajan en todas direcciones. El objetivo aquí es estudiar estas ondas viajeras y comprenderlas mejor.

Ondas

Las ondas son perturbaciones reales que se mueven sin la transferencia real de materia. Estas ondas transportan energía y el patrón de perturbación tiene información que se propaga de un punto a otro. Todas las comunicaciones en nuestra vida diaria, como las señales telefónicas, Internet, son en realidad ondas de información que viajan a través de diferentes medios para llegar a los usuarios. Estas ondas se pueden clasificar en dos categorías diferentes en función de su forma de propagación:

Ondas transversales: las partículas del medio oscilan perpendicularmente a la dirección de movimiento de la onda.

Ondas longitudinales : las partículas del medio oscilan a lo largo de la dirección de propagación del movimiento de la onda.

Velocidad de una onda

Dado que las partículas del medio realizan una oscilación de un lado a otro en la onda, estas ondas se pueden describir matemáticamente en términos de funciones trigonométricas similares a los movimientos armónicos simples (MAS). Por conveniencia, se considera que la onda es una onda transversal, de modo que si la posición de los constituyentes del medio se denota por x, el desplazamiento desde la posición de equilibrio se puede denotar por y. Entonces, la onda sinusoidal se puede representar por,

y(x, t) = Asen(kx – t)

Suponga que la onda conserva su forma mientras se mueve. Para un punto fijo, la onda debe tener un argumento constante para la función sinusoidal. De este modo,

kx – t = constante

Por lo tanto, diferenciándolo con el tiempo para encontrar la velocidad.

$\frac{d}{dt}(kx - ωt) = \frac{d}{dt}(constant) \\ = k\frac{dx}{dt} - \omega = 0 \\ = \frac{dx}{dt} = \frac{\omega}{k}$

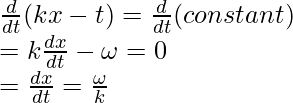
Esta ecuación representa la velocidad de la onda viajera. Consideremos algunos casos especiales,

Velocidad de una onda transversal en una cuerda estirada

En el caso de una cuerda estirada, la velocidad de la onda depende de dos factores: la densidad de masa lineal por unidad de longitud y la tensión de la cuerda. La densidad de masa lineal por unidad de longitud se define como la masa por unidad de longitud de la cuerda. Suponiendo que la tensión en la onda es “T”. Entonces, la velocidad de la onda está dada por,

$v = \sqrt{\frac{T}{\mu}}$

Velocidad de la onda sonora en el aire

Se sabe que el sonido viaja en forma de compresiones y rarefacciones en el aire. La propiedad que determina el grado de compresión y rarefacción en cualquier medio se denomina módulo de volumen (B). está dado por,

$B = - \frac{\Delta P}{\frac{\Delta V}{V}}$

El término anterior representa cuánto cambio hay en el volumen al cambiar la presión en un valor finito. El $\frac{\Delta V}{V}$ representa el cambio fraccionario en el volumen al cambiar la presión por $\Delta P$ .

Por lo tanto, la velocidad del sonido mientras viaja en un medio está dada por,

$v = \sqrt{\frac{B}{\rho}}$

Donde rho, representa la densidad del medio.

Problemas de muestra

Pregunta 1: Encuentra el medio en el que las ondas viajarán más rápido:

(1) H₂

(2) N ₂

(3) el

_{( 4} ) O2

Responder:

La velocidad de la onda que viaja en un medio está dada por,

$v = \sqrt{\frac{B}{\rho}}$

Observe que la velocidad de la onda es inversamente proporcional a la densidad del medio.

De todas las opciones dadas, la masa molecular de H₂ es la menor para volúmenes iguales de gases. Así, la densidad para este medio es la mínima.

Por lo tanto, las ondas viajarán más rápido en el H₂ _.

Por lo tanto, la respuesta es (1).

Pregunta 2: Encuentre la velocidad de la onda que viaja por una cuerda estirada de tensión T = 50 N y densidad de masa de 500 g/m.

Responder:

La velocidad de la onda que viaja en una cuerda está dada por,

$v = \sqrt{\frac{T}{\mu}}$

Aquí, T = 50N y

Sustituyendo los valores en la ecuación,

$v = \sqrt{\frac{T}{\mu}}$

⇒ $v = \sqrt{\frac{50}{0.5}}$

⇒ v = √100

⇒ v = 10 m/s.

Pregunta 3: Encuentre la velocidad de la onda que viaja por una cuerda estirada de tensión T = 100 N y densidad de masa de 2 kg/m.

Responder:

La velocidad de la onda que viaja en una cuerda está dada por,

$v = \sqrt{\frac{T}{\mu}}$

Aquí, T = 100 N y μ = 2 kg/m.

Sustituyendo los valores en la ecuación,

$v = \sqrt{\frac{T}{\mu}}$

⇒ $v = \sqrt{\frac{100}{2}}$

⇒v = √50

⇒ v = 5√2 m/s.

Pregunta 4: Encuentre la velocidad de la onda que viaja en un medio cuyo módulo aparente B es 1.01 × 10 ⁵ N/m ² y la densidad es 1.29 Kg/m ³ .

Responder:

La velocidad de la onda que viaja en un medio está dada por,

$v = \sqrt{\frac{B}{\rho}}$

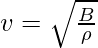
Aquí, B = 1,01 × 10 ⁵ N/m ² y ρ = 1,29 kg/m.

Sustituyendo los valores en la ecuación,

$v = \sqrt{\frac{B}{\rho}}$

⇒ $v = \sqrt{\frac{1.01 \times 10^5}{1.29}}$

⇒ v = 280 m/s

Pregunta 5: Encuentre la velocidad de la onda que viaja en un medio cuyo módulo aparente B es 6 × 10 ⁶ N/m ² y la densidad es 1.5 Kg/m ³ .

Responder:

La velocidad de la onda que viaja en un medio está dada por,

$v = \sqrt{\frac{B}{\rho}}$

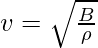
Aquí, B = 6 × 10 ⁶ N/m ² y ρ = 1,5 kg/m.

Sustituyendo los valores en la ecuación,

$v = \sqrt{\frac{B}{\rho}}$

⇒ $v = \sqrt{\frac{6 \times 10^6}{1.5}}$

⇒ v = 400 m/s

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Ondas

Velocidad de una onda

Problemas de muestra

Deja una respuesta Cancelar la respuesta