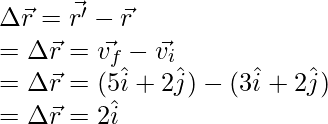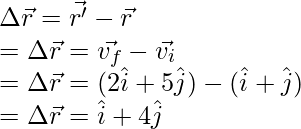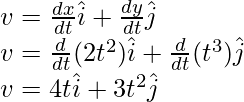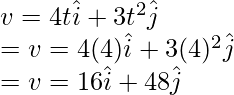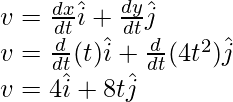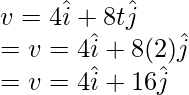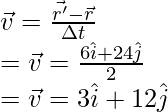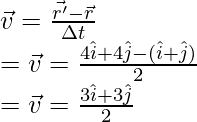Velocidad media – Barcelona Geeks

Es fundamental saber describir el movimiento de un cuerpo o de una partícula. Estas convenciones y métodos nos permiten formalizar y luego usarlos para desarrollar más teoría. La velocidad es la noción de qué tan rápido se mueve una partícula. Se usa casi todos los días y denota la tasa de cambio de posición de un objeto. En teoría, es esencial describir la velocidad y la dirección de la partícula de manera formal. Esto se hace usando vectores y esto se llama velocidad. Veamos este concepto en detalle.

Movimiento en un plano

Cuando una partícula se mueve de un punto a otro punto en los ejes X e Y. Se dice que se mueve en un avión. Un plano se compone de ejes X e Y, que se utilizan para indicar la posición de la partícula. El movimiento en un plano también se describe en términos de las coordenadas X e Y de las partículas y qué tan rápido están cambiando. El movimiento se puede trazar en un plano cartesiano como se muestra en la siguiente figura.

El movimiento de cualquier partícula que se mueve en un plano se puede describir utilizando su posición y su velocidad.

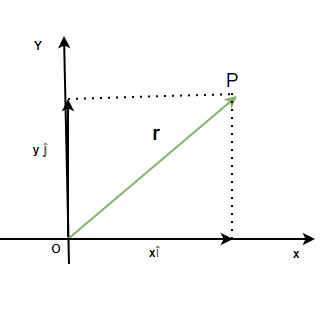
Vector de posición

El vector de posición se utiliza para indicar la posición de la partícula en el plano cartesiano con respecto al origen como referencia. El vector $\vec{r}$ de posición de una partícula está dado por,

$\vec{r} = x\hat{i} + y\hat{j}$

Donde x e y son sus componentes a lo largo del eje x e y.

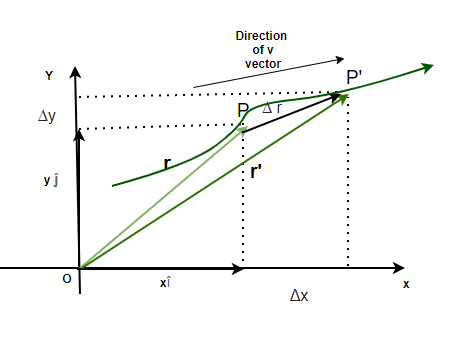
Supongamos que una partícula se mueve de $\vec{r}$ a $\vec{r'}$ . Entonces el desplazamiento se dirige hacia,

$\Delta \vec{r} = \vec{r'} - \vec{r}$

Velocidad

La velocidad media es la relación entre el desplazamiento total y el tiempo total. Supongamos que una partícula va de $\vec{r}$ a $\vec{r'}$ en un tiempo total de $\Delta t$

La velocidad está dada por,

$\vec{v} = \frac{\vec{r} - \vec{r'}}{\Delta t}$

Esto supone que la velocidad de un objeto es constante, pero a menudo este no es el caso. A veces, la velocidad cambia con el tiempo. En ese caso, se debe calcular la velocidad instantánea. está dado por,

$\vec{v} = \lim_{\Delta t \to 0}\frac{\Delta \vec{r}}{\Delta t}\\ = \vec{v} = \frac{dr}{dt}$

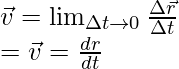
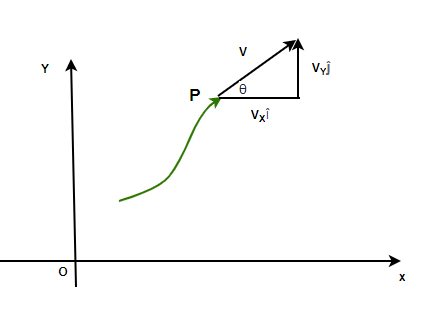
La dirección de la velocidad de una partícula que sigue una trayectoria en cualquier punto está dada por una tangente trazada en ese punto particular en la dirección del movimiento. La velocidad también se puede expresar en forma de sus componentes.

$v = \frac{dr}{dt} \\ = v = \lim_{\Delta t \to 0}(\frac{\Delta x}{\Delta t} + \frac{\Delta y}{\Delta t}) \\ = v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j}$

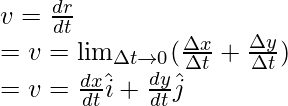
Entonces, si se conocen los componentes de una velocidad, la magnitud de la velocidad se puede calcular usando,

$v = \sqrt{v_x^2 + v_y^2}$

Y la dirección viene dada por el ángulo $\theta$ ,

$\theta = tan^{-1}(\frac{v_x}{v_y})$

Veamos algunos ejemplos de problemas.

Problemas de muestra

Pregunta 1: Encuentre el vector de desplazamiento para la partícula que se mueve en un plano y cuyos vectores de posición se dan a continuación,

v _i = 3i + 4j y v _f = 5i + 2j

Responder:

Dados: los vectores de posición inicial y final,

v _yo = 3i + 4j

v _f = 5i + 2j

El objetivo es encontrar el vector de desplazamiento. está dado por,

$\Delta \vec{r} = \vec{r'} - \vec{r}$

aquí $\vec{r} = \vec{v_i}$ y $\vec{r'} = \vec{v_f}$

Reemplazando estos valores en la ecuación,

$\Delta \vec{r} = \vec{r'} - \vec{r} \\ =\Delta \vec{r} = \vec{v_f} - \vec{v_i}\\ = \Delta \vec{r} = (5\hat{i} + 2\hat{j}) - (3\hat{i} + 2\hat{j}) \\ = \Delta \vec{r} = 2\hat{i}$

Pregunta 2: Encuentre el vector de desplazamiento para la partícula que se mueve en un plano y cuyos vectores de posición se dan a continuación,

v _yo = yo + j y v _f = 2i + 5j

Responder:

Dados: los vectores de posición inicial y final,

v _yo = yo + j

v _f = 2i + 5j

El objetivo es encontrar el vector de desplazamiento. está dado por,

$\Delta \vec{r} = \vec{r'} - \vec{r}$

aquí $\vec{r} = \vec{v_i}$ y $\vec{r'} = \vec{v_f}$

Reemplazando estos valores en la ecuación,

$\Delta \vec{r} = \vec{r'} - \vec{r} \\ =\Delta \vec{r} = \vec{v_f} - \vec{v_i}\\ = \Delta \vec{r} = (2\hat{i} + 5\hat{j}) - (\hat{i} + \hat{j}) \\ = \Delta \vec{r} = \hat{i} + 4\hat{j}$

Pregunta 3: Encuentra la velocidad en t = 4, para la partícula que se mueve en un plano y cuya posición se da a continuación,

r = 2t ² yo + t ³ j

Responder:

Dados: los vectores de posición inicial y final,

r = 2t ² yo + t ³ j

El vector de posición cambia con el tiempo. La velocidad en este caso está dada por la fórmula,

$v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j}$

Aquí x(t) = 2t ² y y(t) = t ³

Reemplazando estos valores en la ecuación,

$v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j} \\ v= \frac{d}{dt}(2t^2)\hat{i} + \frac{d}{dt}(t^3)\hat{j} \\ v = 4t \hat{i} + 3t^2\hat{j}$

En t = 4,

$v = 4t \hat{i} + 3t^2\hat{j} \\ = v = 4(4)\hat{i} + 3(4)^2\hat{j} \\ = v = 16\hat{i} + 48\hat{j}$

Pregunta 4: Encuentra la velocidad en t = 2, para la partícula que se mueve en un plano y cuya posición se da a continuación,

r = ti + 4t ² j

Responder:

Dados: los vectores de posición inicial y final,

r = ti + 4t ² j

El vector de posición cambia con el tiempo. La velocidad en este caso está dada por la fórmula,

$v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j}$

Aquí x(t) = t y y(t) = 4t ²

Reemplazando estos valores en la ecuación,

$v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j} \\ v= \frac{d}{dt}(t)\hat{i} + \frac{d}{dt}(4t^2)\hat{j} \\ v = 4\hat{i} + 8t\hat{j}$

en t = 4,

$v = 4\hat{i} + 8t\hat{j} \\ = v = 4\hat{i} + 8(2)\hat{j} \\ = v = 4\hat{i} + 16\hat{j}$

Pregunta 5: Encuentra la velocidad promedio entre t = 0 y t = 2, para la partícula que se mueve en un plano y cuya posición se da a continuación,

r = 3ti + 3t ^3j

Responder:

Dados: los vectores de posición inicial y final,

r = 3ti + 3t ^3j

El vector de posición cambia con el tiempo. La velocidad media viene dada por la fórmula,

$\vec{v} = \frac{\vec{r} - \vec{r'}}{\Delta t}$

En t = 0

r = 0i + 0j

En t = 2

r’ = 6i + 24j

$\Delta t = 2$

Conectando los valores en esta ecuación anterior,

$\vec{v} = \frac{\vec{r'} - \vec{r}}{\Delta t}\\ = \vec{v} = \frac{6\hat{i} + 24\hat{j}}{2} \\ = \vec{v} = 3\hat{i} + 12\hat{j}$

Pregunta 6: Encuentra la velocidad promedio entre t = 1 y t = 4, para la partícula que se mueve en un plano y cuya posición se da a continuación,

r = ti + tj

Responder:

Dados: los vectores de posición inicial y final,

r = ti + tj

El vector de posición cambia con el tiempo. La velocidad media viene dada por la fórmula,

$\vec{v} = \frac{\vec{r} - \vec{r'}}{\Delta t}$

En t = 1

r = 1i + 1j

En t = 4

r’ = 4i + 4j

$\Delta t = 3$

Conectando los valores en esta ecuación anterior,

$\vec{v} = \frac{\vec{r'} - \vec{r}}{\Delta t}\\ = \vec{v} = \frac{4\hat{i} + 4\hat{j} - (\hat{i} + \hat{j})}{2} \\ = \vec{v} = \frac{3\hat{i} + 3\hat{j}}{2}$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Movimiento en un plano

Problemas de muestra

Deja una respuesta Cancelar la respuesta