La distribución gaussiana (más conocida como distribución normal) es una de las distribuciones de probabilidad más fundamentales en estadística. Una distribución gaussiana bivariada consta de dos variables aleatorias independientes. Uno puede notar una curva de campana mientras visualiza una distribución gaussiana bivariada. Dos variables aleatorias X 1 y X 2 son normales bivariadas si aX 1 +bX 2 tiene una distribución normal para todo a, b ∈ R.
Función de distribución de probabilidad (PDF) de una distribución gaussiana bivariada
La función de densidad describe la probabilidad relativa de una variable aleatoria X en una muestra dada. Matemáticamente, la PDF de dos variables X e Y en una distribución gaussiana bivariada viene dada por:
![Rendered by QuickLaTeX.com P(x_{1},x_{2})=\frac{1}{2\pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^2}} \exp{ \left[ \frac{-z}{2(1-\rho^2)}\right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-783b8278081815000e0fd0bf15473d14_l3.png)
dónde,
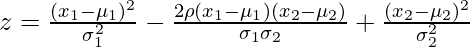
- μ = media
- σ = desviación estándar
- ρ = correlación de x 1 y x 2
Si P = 2, entonces esta es una distribución gaussiana bivariada.
Visualización de la distribución gaussiana bivariada en R
Visualizaremos la distribución gaussiana bivariada en R al trazarlas usando las funciones del paquete mnormt() .
install.packages('mnormt')
Usaremos dmnorm() para simular una distribución normal.
dmnorm( ): mnorm(x, media = rep(0, d), varcov, log = FALSO)
| Parámetro | Descripción |
|---|---|
| X | un vector de longitud d donde ‘d=ncol(varcov)’. |
| significar | el valor esperado de la distribución. |
| várcov | array de varianzas-covarianzas de la distribución. |
| Iniciar sesión | si ‘VERDADERO’ calcula el logaritmo de la densidad. |
Ahora, usaremos la función de contorno() para crear un gráfico de contorno, para obtener una visualización en 2-D de la distribución gaussiana bivariada
R
library(mnormt) set.seed(0) x1 <- seq(-4, 4, 0.1) x2 <- seq(-5, 5, 0.1) mean <- c(0, 0) cov <- matrix(c(2, -1, -1, 2), nrow=2) f <- function(x1, x2) dmnorm(cbind(x1, x2), mean, cov) y <- outer(x1, x2, f) # create contour plot contour(x1, x2, y)
n : sample size. mean : mean of each variable. cov : covariance matrix of the two variables.
Producción:

Para la visualización en 3D de la distribución, crearemos un gráfico de superficie utilizando la función persp() del paquete.
persp(x = seq(0, 1, length.out = nrow(z)),y = seq(0, 1, length.out = ncol(z)),z, xlim = rango(x), ylim = rango (y),zlim = range(z, na.rm = TRUE),xlab = NULL, ylab = NULL, zlab = NULL,main = NULL, sub = NULL,theta = 0, phi = 15, r = sqrt(3 ), d = 1, escala = VERDADERO, expandir = 1, columna = «blanco», borde = NULO, theta = -135, lphi = 0, sombra = NA, caja = VERDADERO, ejes = VERDADERO, marcas = 5, tipo de marca = “sencillo”, …)
| Parámetro | Descripción |
|---|---|
| x, y | ubicación de las líneas de cuadrícula. |
| xlim, ylim, zlim | límites x, y y z. |
| xlab, ylab, zlab | títulos para los ejes. |
| theta, fi | ángulos que definen la dirección de visualización. |
| expandir | un factor de expansión aplicado a las coordenadas z. |
| columna | el color(es) de las facetas de la superficie. |
| borde | el color de la línea dibujada alrededor de las facetas de la superficie. |
| sombra | la sombra en una faceta de la superficie. |
| caja | debe mostrarse el cuadro delimitador de la superficie. |
| tipo de garrapata | tipos de garrapatas. |
R
install.packages('mnormt')
library(mnormt)
set.seed(0)
x1 <- seq(-4, 4, 0.1)
x2 <- seq(-5, 5, 0.1)
mean <- c(0, 0)
cov <- matrix(c(2, -1, -1, 2), nrow=2)
f <- function(x1, x2) dmnorm(cbind(x1, x2), mean, cov)
y <- outer(x1, x2, f)
#create surface plot
persp(x1, x2, y, theta=-20, phi=20, col = 'blue',
expand=0.8, ticktype='detailed')
Producción:

Publicación traducida automáticamente
Artículo escrito por misraaakash1998 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA