Un sólido de revolución se genera haciendo girar un área plana R alrededor de una línea L conocida como eje de revolución en el plano. La imagen de abajo muestra un ejemplo de sólido de revolución.

Calcularemos el volumen del sólido de revolución cuando la ecuación de la curva esté dada en forma paramétrica y forma polar.
- Forma Paramétrica:
Si la ecuación de la curva en forma paramétrica está dada por:x= f(t) and y= g(t)
Donde t varía de t 1 a t 2 , entonces el volumen de revolución:
- Sobre el eje x –
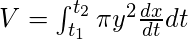

- Sobre el eje y –
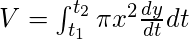
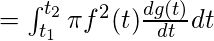
- Sobre el eje x –
- Forma polar:
Dada la ecuación de la curva en forma polar como r=f(θ), donde θ varía de θ 1 a θ 2 , el volumen de revolución se calcula usando las fórmulas dadas:- Sobre la línea inicial OX, es decir, el eje x (θ=0) –
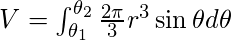
- Sobre la línea perpendicular a la línea inicial, es decir, a lo largo de OY (θ=π/2) –
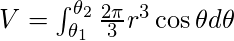
- Sobre la línea inicial OX, es decir, el eje x (θ=0) –
Veamos los siguientes ejemplos.
Ejemplo-1:
Determine el volumen del sólido de revolución generado al girar la curva cuyas ecuaciones paramétricas son:
X= 2t+3 and y= 4t2-9
Sobre el eje x para t= -3/2 a 3/2.
Explicación:
sabemos que el volumen del sólido que gira alrededor del eje x cuando la ecuación está en forma paramétrica viene dado por ![]()
![]()
Usando este valor obtenemos![]()
![]()
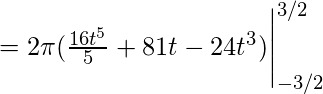
![]()
Ejemplo-2:
Encuentre el volumen de sólido generado por la curva giratoria r= 2a cos θ sobre la línea inicial OX.
Explicación:
sabemos que el volumen de sólido generado al girar alrededor de OX cuando la ecuación está en forma polar viene dado por ![]()
También para OX, θ=0
Entonces , ![]()
![]()
usando ![]()
![]()
estos valores, obtenemos![]()

![]()