Puntuación Z en estadísticas

En este artículo, vamos a discutir los siguientes conceptos,  

• ¿Qué es un puntaje Z?
• Fórmula para Z-Score
• ¿Cómo calcular la puntuación Z?
• Interpretación de la puntuación Z

¿Qué es un puntaje Z? 

La puntuación Z, también conocida como puntuación estándar , nos da una idea de qué tan lejos está un punto de datos de la media. Indica a cuántas desviaciones estándar se encuentra un elemento de la media. Por lo tanto, Z-Score se mide en términos de desviación estándar de la media. Por ejemplo, una desviación estándar de 2 indica que el valor está a 2 desviaciones estándar de la media. Para usar un puntaje z, necesitamos conocer la media de la población (μ) y también la desviación estándar de la población (σ). 

La fórmula para la puntuación Z

Una puntuación z se puede calcular usando la siguiente fórmula. 
 

z = (X – μ) / σ

donde, 
z = puntuación Z, 
X = el valor del elemento, 
μ = la media de la población y 
σ = la desviación estándar de la población 
 

¿Cómo calcular la puntuación Z?

Por lo general, la media de la población ((μ), la desviación estándar de la población (σ) y el valor observado (x) se proporcionan en el enunciado del problema, y ​​al sustituir lo mismo en la ecuación de puntaje Z anterior, obtenemos el valor de puntaje Z Dependiendo de si el Z-Score dado es positivo o negativo, uno hace uso de la respectiva Tabla Z positiva o Tabla Z negativa disponible en línea o en la parte posterior de su libro de texto de estadística en el apéndice.

Ejemplo:  

Pregunta: 
Usted toma el examen GATE y obtiene un puntaje de 500. El puntaje promedio para el GATE es 390 y la desviación estándar es 45. ¿Qué tan bien obtuvo su puntaje en el examen en comparación con el examinado promedio? 

Solución: 
Los siguientes datos están fácilmente disponibles en el enunciado de la pregunta anterior 
Puntuación bruta/valor observado = X = 500 
Puntuación media = μ = 390 
Desviación estándar = σ = 45 

Al aplicar la fórmula de la puntuación z,  

z = (X – μ) / σ 
z = (500 – 390) / 45 
z = 110 / 45 = 2,44

Esto significa que su puntaje z es 2.44 . 

Dado que el Z-Score es positivo 2.44, utilizaremos la Z-Table positiva. 

Ahora echemos un vistazo a la Tabla Z (CC-BY) para saber qué tan bien obtuvo su puntaje en comparación con los otros examinados.

Siga las instrucciones a continuación para encontrar la probabilidad de la tabla.

Aquí,   puntuación z = 2,44

1. En primer lugar, asigne los primeros dos dígitos 2.4 en el eje Y.
2. Luego, a lo largo del eje X, mapee 0.04
3. Une ambos ejes. La intersección de los dos le proporcionará el valor Z-Score que está buscando

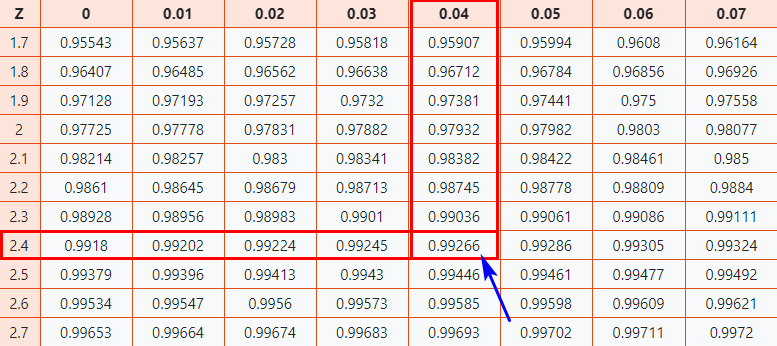
Como resultado, obtendrá el valor final que es 0.99266 .

Ahora, necesitamos comparar cómo nuestro puntaje original de 500 en el examen GATE se compara con el puntaje promedio del lote. Para hacer eso, necesitamos convertir el Z-Score en un valor porcentual.

0.99266 * 100 = 99.266%

Finalmente, puede decir que se ha desempeñado mejor que casi el 99% de los demás examinados.

Interpretación de la puntuación Z 

• Un elemento que tiene una puntuación z inferior a 0 representa que el elemento es inferior a la media.
• Un elemento que tiene una puntuación z mayor que 0 representa que el elemento es mayor que la media.
• Un elemento que tiene un puntaje z igual a 0 representa que el elemento es igual a la media.
• Un elemento que tiene una puntuación z igual a 1 representa que el elemento es 1 desviación estándar mayor que la media; una puntuación z igual a 2, 2 desviaciones estándar mayor que la media, y así sucesivamente.
• Un elemento que tiene una puntuación z igual a -1 representa que el elemento tiene 1 desviación estándar menos que la media; un puntaje z igual a -2, 2 desviaciones estándar menos que la media, y así sucesivamente.
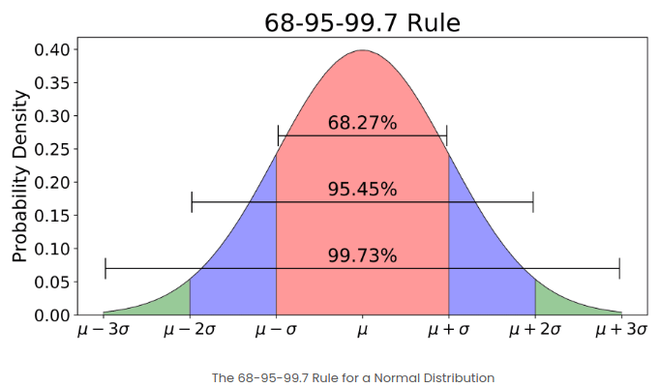
• Si el número de elementos en un conjunto dado es grande, alrededor del 68 % de los elementos tienen una puntuación z entre -1 y 1; alrededor del 95 % tiene una puntuación z entre -2 y 2; aproximadamente el 99 % tiene un puntaje z entre -3 y 3. Esto se conoce como la regla empírica o la regla 68-95-99.7 y se puede demostrar en la siguiente imagen