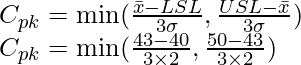Fórmula Cp de capacidad de proceso

Un proceso es una serie de pasos/tareas para convertir una entrada en una salida. La capacidad , por otro lado, significa producir algo con un conjunto de especificaciones de manera consistente. Por lo tanto, decimos que la capacidad del proceso es una medida estadística de la capacidad de un proceso para producir partes de la especificación deseada de manera consistente.

Con la ayuda de datos históricos, obtenemos la respuesta a la pregunta: «¿Puede este proceso producir diariamente piezas con las especificaciones deseadas?». Gráfico de control de estudios de capacidad de proceso, que ayuda a determinar si un proceso está en un estado controlado o no controlado.

Antes de profundizar en varios conceptos, háganos saber algunas definiciones básicas

Límite de especificación superior : este es el límite más alto o el límite superior de una medición o lectura
Límite de especificación inferior : este es el límite más bajo o el límite inferior de una medición o lectura
Límite de control superior: el límite superior de la línea de control, cualquier lectura por encima de esto debe investigarse en busca de variaciones inusuales.
Límite de control inferior: el límite inferior de la línea de control, cualquier lectura por debajo de este debe investigarse en busca de variaciones inusuales.

C _p y el índice C _pk

Para cualquier proceso, el objetivo final es tener un gráfico de control que sea

Centrado alrededor del valor medio o nominal
Extendido sobre un ancho de especificación estrecho

Para lograr esto nos ayudamos de C _p y el índice C _pk o también llamados índices de Capacidad de Proceso .

La fórmula para ambos es la siguiente:

$C_p = \frac{\text{Specification Width}}{\text{Process Width}} = \frac{\text{USL - LSL}}{\text{UCL-LCL}} = \frac{\text{USL - LSL}}{6\sigma}\\$

$C_{pk} = \frac{\text{Distance from mean to nearest spec limit}}{\text{Distance of mean to control limit}} = \min({\frac{|\bar{\bar{x}}-UCL|}{3\sigma},{\frac{|\bar{\bar{x}}-LCL|}{3\sigma}}})$

Cp determina la _dispersión del gráfico de control, qué tan estrechos o anchos son los límites de especificación.

C _pk determina la dispersión del gráfico de control en relación con los límites de especificación.

Ahora tomemos una analogía que puede ayudarnos a entender los dos índices.

Consideremos un escenario en el que a un grupo de conductores, todos con una experiencia diferente en la conducción, se les dice que estacionen los autos en un garaje. Todos los coches son idénticos en anchura, es decir, su especificación (al menos la anchura) es la misma y esta anchura es menor que la del garaje (pero no mucho).

En este C _p determina el ancho de la cola de automóviles y C _pk determina qué tan centrales están a la puerta del garaje

No caso.	CP	Cpk	Resultado
Caso 1	Cp < 0,7	Cpk < 0,7	Aquí el ancho de la cola es estrecho (Cp<0.5) pero los autos no están en el centro (Cpk<0.5), por lo que los autos no caben adentro, lo que hace que este caso no sea apto.
Caso 2	0,7<CP<1,33	0.7<Cpk<1.33	Aquí el ancho de la cola es menor que en el caso anterior, y los autos están relativamente más céntricos, por lo que los autos simplemente caben adentro, lo que hace que este caso sea apenas capaz
Caso 3	Cp>1.33	Cpk < 0,7	Aquí el ancho de la cola es mínimo, pero los autos no están en el centro, por lo que los autos no cabrían dentro, lo que hace que este caso no sea capaz.
Caso 4	Cp>1.33	Cpk>1.33	Aquí, el ancho de la cola es mínimo y los autos están lo más céntricos posible, por lo que los autos cabrían fácilmente en el interior, lo que hace que este caso sea capaz

Nota: estos son solo números arbitrarios, solo dan una analogía.

De la tabla anterior, podemos concluir que tener un Cp y un Cpk más altos siempre es una mejor opción, ya que reduce el gráfico de control acercando todas las lecturas a la media y también centralizándola entre los dos límites de control. Esto asegura que la cantidad de productos/piezas defectuosas sea la menor posible.

Problemas de muestra

Problema 1: La comida que se sirve en un restaurante debe estar entre 40 °C y 50 °C cuando se entrega al cliente. El proceso utilizado para mantener los alimentos a la temperatura correcta tiene una desviación estándar de proceso de 2 °C y el valor medio de estas temperaturas es 43. ¿Cuál es el índice de capacidad de proceso del proceso?

Solución:

$\bar{x}$ = 43

USL = 50

LEI = 40

σ = 2

$C_{pk} = \min(\frac{\bar{x}-LSL}{3\sigma},\frac{USL-\bar x}{3\sigma})\\ C_{pk} = \min(\frac{43-40}{3\times 2},\frac{50-43}{3\times 2})$

_pico C = min (0,5, 1,16)

= 0,5

Problema 2: Calcular el C _p de un gráfico de control cuyos USL, LSL y SD son 15,5,2 respectivamente.

Solución:

USL = 15

LEI = 5

σ = 2

$C_p = \frac{\text{USL} -\text{LSL}}{6\times \sigma}\\ C_p = \frac{15-5}{6\times 2}$

C _p = 10/12

= 0,833

Problema 3: Un gráfico de control de una empresa da las siguientes lecturas;

Parámetro	Lectura
USL	117
UCL	71
LSL	37
LCL	43
Desviación Estándar	4.68
Significar	53

Calcular los índices de capacidad del proceso (C _p y C _pk )

Solución:

De la tabla vemos que

USL = 117

LCC = 71

LCl = 43

LEI = 37

σ = 4,68

$\bar{x}$ = 53

$C_p = \frac{\text{USL}-\text{LSL}}{\text{UCL}-\text{LCL}}\\ C_p = \frac{117-37}{71-43} = 2.85\\ C_{pk} = \min(\frac{\bar{x}-LSL}{3\sigma},\frac{USL-\bar x}{3\sigma})\\ C_{pk} = \min(\frac{53-37}{3\times 4.68},\frac{117-53}{3\times4.68})$

_pico C = min (1,14, 4,55)

= 1,14

Publicación traducida automáticamente

Artículo escrito por sohamsinghal32 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C p y el índice C pk

Problemas de muestra

Deja una respuesta Cancelar la respuesta

C _p y el índice C _pk