La pirámide es una estructura geométrica tridimensional con base poligonal y todas sus caras triangulares se encuentran en un punto común llamado vértice o vértice. Los ejemplos de pirámides de la vida real son las pirámides de Egipto; tejados; tiendas de campaña, etc. Dependiendo de la forma de la base poligonal, las pirámides se clasifican en diferentes tipos, como pirámides triangulares, pirámides cuadradas, pirámides rectangulares, etc. Las caras laterales, o superficies laterales de una pirámide, son triángulos que se encuentran en un punto común llamado vértice. La altura, o altitud, de una pirámide es la distancia perpendicular entre el vértice y el centro de la base, mientras que la altura inclinada es la distancia perpendicular entre el vértice y la base de una superficie lateral.

Área de superficie de una pirámide
El área de superficie de una pirámide es la suma de las áreas de las superficies laterales, o caras laterales, y la base de una pirámide. La superficie de una pirámide tiene básicamente dos tipos de superficies: la superficie lateral y la superficie total, y se miden en términos de m 2 , cm 2 , in 2 , ft 2 , etc.
Área de superficie lateral de una pirámide (LSA) = Suma de áreas de las superficies laterales (triángulos) de la pirámide
Superficie total de una pirámide (TSA) = Superficie lateral de la pirámide + Área de la base
Para determinar la superficie lateral de una pirámide, se calculan las áreas de las caras laterales (triángulos) y se suman los resultados, mientras que el área de superficie total de una pirámide se calcula sumando el área de la base de la pirámide y el área de superficie lateral.

Área de superficie de una pirámide triangular

Una pirámide triangular es una pirámide que tiene una base triangular, donde la base triangular puede ser equilátera, isósceles o un triángulo escalar. Tiene tres caras laterales (triangulares) y una base triangular.
Lo sabemos,
El área de superficie total de una pirámide (TSA) = Área de superficie lateral de la pirámide + Área de la base
Área de superficie lateral (LSA) = ½ × perímetro × altura inclinada
Entonces, TSA = ½ × perímetro × altura inclinada + ½ × base × altura
Área de superficie total (TSA) de una pirámide triangular = ½ × P × l + ½ bh
dónde,
P es el perímetro de la base
l es la altura inclinada de la pirámide
b es base del triangulo base
h es la altura de la pirámide
Área de superficie de una pirámide cuadrada

Una pirámide cuadrada es una pirámide que tiene una base cuadrada. Tiene cuatro caras laterales (triangulares) y una base cuadrada.
Lo sabemos,
El área de superficie total de una pirámide (TSA) = Área de superficie lateral de la pirámide + Área de la base
La altura inclinada de la pirámide (l) = √[(a/2) 2 + h 2 ]
LSA = 4 × [½ × un × l] = 2al
Superficie lateral de la pirámide cuadrada (LSA)= 2al
Entonces, TSA = 2al + a 2
Superficie total de una pirámide cuadrada (TSA) = 2al + a 2
dónde,
a es lado de base cuadrada
l es la altura inclinada de la pirámide
Superficie de una pirámide rectangular
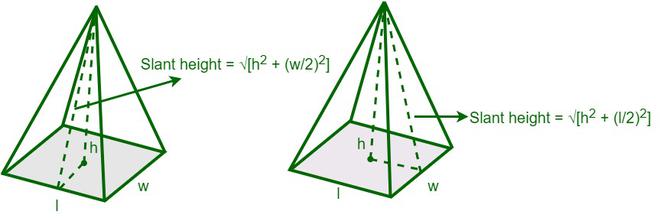
Una pirámide rectangular es una pirámide que tiene una base rectangular. Tiene cuatro caras laterales (triangulares) y una base rectangular.
Lo sabemos,
El área de superficie total de una pirámide (TSA) = Área de superficie lateral de la pirámide + Área de la base
La altura inclinada de la cara longitudinal de la pirámide = √[h 2 + (l/2) 2 ]
La altura inclinada de la cara ancha de la pirámide = √[h 2 + (w/2) 2 ]
Área de la superficie lateral de una pirámide rectangular = 2 × {½ × l ×√[h 2 + (l/2) 2 ]} + 2 × {½ × w ×√[h 2 + (w/2) 2 ]
Asi que,
Área de superficie total de la pirámide rectangular = 2 × {½ × l ×√[h 2 + (l/2) 2 ]} + 2 × {½ × w ×√[h 2 + (w/2) 2 ] + l × ancho
dónde,
l es la longitud de la base del rectángulo
w es el ancho de la base del rectángulo
h es la altura de la pirámide
Área de superficie de una pirámide pentagonal

Una pirámide pentagonal es una pirámide que tiene una base pentagonal. Tiene cinco caras laterales (triangulares) y una base pentagonal.
Lo sabemos,
El área de superficie total de una pirámide (TSA) = Área de superficie lateral de la pirámide + Área de la base
La longitud de la apotema de la base = a
La longitud del lado de la base = s
La altura inclinada de la pirámide = l
El área de la base pentagonal = 5⁄2 (a × s)
Ahora,
LSA = 5 × [½ × base × altura] = 5/2 × s × l
Área de la superficie lateral de la pirámide pentagonal = 5⁄2 (s × l)
Área de superficie total de la pirámide pentagonal = 5⁄2 (s × l) + 5⁄2 (a × s)
dónde,
l es la altura inclinada de la pirámide
una apotema longitud de la base
longitud del lado s de la base
Superficie de una pirámide hexagonal

Una pirámide hexagonal es una pirámide que tiene una base hexagonal. Tiene seis caras laterales (triangulares) y una base hexagonal.
Lo sabemos,
El área de superficie total de una pirámide (TSA) = Área de superficie lateral de la pirámide + Área de la base
La longitud del lado de la base = s
La altura inclinada de la pirámide = l
Área de la base hexagonal = 3√3/2 (s) 2
Ahora,
LSA = La suma de las áreas de las superficies laterales (triángulos) de la pirámide
= 6 × [½ × base × altura] =3(s × l)
Área de la superficie lateral de la pirámide hexagonal = 3(s × l)
Superficie total de la pirámide hexagonal = 3(s × l) + 3√3/2 (s) 2
dónde,
s es la longitud del lado de la base
l es la altura inclinada de la pirámide
Problemas de muestra
Problema 1: Determine el área de superficie de una pirámide cuadrada si la longitud del lado de la base es de 16 pulgadas y la altura inclinada de la pirámide es de 18 pulgadas.
Solución:
Dado,
El lado de la base cuadrada (a) = 16 pulgadas, y
Altura inclinada, l = 18 pulgadas
El perímetro de la base cuadrada (P) = 4a = 4(16) = 64 pulgadas
El área de la superficie lateral de una pirámide cuadrada = (½) Pl
LSA = (½ ) × (64) × 18 = 576 pulgadas cuadradas
Ahora, el área de superficie total = Área de la base + LSA
= un 2 + LSA
= (16) 2 + 576 = 832 pulgadas cuadradas
Por lo tanto, el área de la superficie de la pirámide dada es de 832 pulgadas cuadradas.
Problema 2: Una caja tiene la forma de una pirámide triangular, y cada cara de la caja tiene la forma de un triángulo equilátero. Ahora, determine el área total de la superficie de una pirámide triangular si la longitud del lado de la base es de 24 cm.
Solución:
Dados los datos,
El lado de la base (a) = 24 pulgadas, y
Lo sabemos,
El área de la superficie total de una pirámide (TSA) = Área de la base + Área de las caras laterales
Tenemos,
Área de un triángulo equilátero = √3/4 (a) 2
Por lo tanto, el área de cada cara triangular = √3/4 (a) 2
= √3/4 (24) 2
= 249.415 cm2
Ahora, TSA = 249,415 + 3 × (249,415) = 997,66 cm2
Por lo tanto, el área de superficie total de la pirámide dada es 997,66 cm2.
Problema 3: Determine el área de la superficie lateral de una pirámide pentagonal si la longitud del lado de la base es de 10 cm y la altura inclinada de la pirámide es de 15 pulgadas.
Solución:
Dado,
El lado de la base pentagonal (a) = 10 pulgadas, y
Altura inclinada, l = 15 pulgadas
El perímetro de la base cuadrada (P) = 5a = 5(10) = 50 cm
El área de la superficie lateral de una pirámide pentagonal es,
Superficie lateral (LSA) = (½) Pl
= (½ ) × (50) × 15
= 375 cm2
Por lo tanto, el área de la superficie lateral de la pirámide dada es de 375 cm2.
Problema 4: Determine el área de superficie de una pirámide hexagonal si la longitud del lado de la base es de 12 pulgadas y la altura inclinada de la pirámide es de 14 pulgadas.
Solución:
Dado,
El lado de la base hexagonal (a) = 12 pulgadas, y
Altura inclinada, l = 14 pulgadas
El perímetro de la base cuadrada (P) = 6a = 6(12) = 72 pulgadas
El área de la superficie de una pirámide pentagonal = Área de la base + Área de las caras laterales
Superficie lateral (LSA) = (½) Pl
= (½ ) × (72) × 14 = 504 pulgadas cuadradas
Área de la base hexagonal = 3√3/2 (a) 2 = 3√3/2 (12) = 374,123 pulgadas cuadradas
El área de la superficie de una pirámide = Área de la base + Área de las caras laterales
= 374,123 pulgadas cuadradas + 504 pulgadas cuadradas = 878,123 pulgadas cuadradas
Por lo tanto, el área de superficie de la pirámide dada es 878.123 pulgadas cuadradas.
Problema 5: Determine la longitud del lado de una pirámide cuadrada si su área de superficie lateral es de 600 pulgadas cuadradas y la altura inclinada de la pirámide es de 20 pulgadas.
Solución:
Dado,
El área de la superficie lateral = 600 pulgadas cuadradas
Altura inclinada, l = 20 pulgadas
Sea “a” la longitud del lado de una base cuadrada.
Ahora, el perímetro de la base (P)= 4a
Lo sabemos
El área de la superficie lateral de una pirámide cuadrada = (½) Pl
⇒ 600 = (½ ) × (4a) × 20
⇒ 80a = 1200 ⇒ a = 15 pulgadas
Por lo tanto, la longitud del lado de la pirámide dada es de 15 pulg.
Publicación traducida automáticamente
Artículo escrito por kiran086472 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA