El álgebra es un tema importante de las matemáticas. Una raíz cuadrada es una operación que se usa en muchas fórmulas y diferentes campos de las matemáticas. Este artículo trata sobre la raíz cuadrada y la fórmula de la raíz cuadrada. La raíz cuadrada de un número es un número elevado al cuadrado que da el número original. Hay varias fórmulas de raíces cuadradas que se analizan en este artículo con sus problemas.
Raíz cuadrada
La raíz cuadrada de un número es un número elevado al cuadrado que da el número original. Es ese factor del número que al elevarlo al cuadrado da el número original. Es el valor de la potencia 1/2 de ese número. La raíz cuadrada de un número se representa como √ .
Ejemplo: raíz cuadrada de 9 ⇒ √9 = ± 3
Aquí, 3 2 = 9
(-3) 2 = 9
El número dentro de la raíz cuadrada se llama radicando y el símbolo de la raíz cuadrada se llama radical.
Métodos para encontrar la raíz cuadrada de un número
Hay dos métodos para encontrar las raíces cuadradas de un número que son muy utilizados en matemáticas. Estos se discuten a continuación.
- Método de factorización prima
- Método de división larga
Método de factorización prima
La descomposición en factores primos es un método en el que un número se representa como el producto de números primos. Luego, la raíz cuadrada del número se multa de acuerdo con el concepto dado.
Para encontrar la raíz cuadrada usando el método de descomposición en factores primos:
Paso 1: Representa el número en sus factores primos utilizando el método de descomposición en factores primos.
Paso 2: Forma el par de los mismos factores.
Paso 3: Toma un factor de cada par y luego encuentra los productos de todos los factores obtenidos al tomar un factor de cada par.
Paso 4: El producto resultante es la raíz cuadrada del número.
Ejemplo del método de factorización prima:
| Método de factorización prima para encontrar la raíz cuadrada | |
|---|---|
| 2 | 196 |
| 2 | 98 |
| 7 | 49 |
| 7 | 7 |
| 1 | |
| Factores primos de 196 = (2×2) × (7×7) | |
| Para la raíz cuadrada, tomamos el producto de 2 de (2×2) y 7 de (7×7) | |
|
La raíz cuadrada de 196 = 2×7 La raíz cuadrada de 196 = 14 |
|
Método de división larga
El método de división larga es un método muy útil para encontrar la raíz cuadrada de un número. La raíz cuadrada de cuadrados imperfectos como 14, 15, 18, etc. se puede encontrar usando el método de división larga. Para encontrar la raíz cuadrada usando el método de división larga, debemos seguir los pasos específicos que se describen a continuación.
Pasos para encontrar la raíz cuadrada de un número usando el método de división larga:
Ejemplo: Encuentra la raíz cuadrada de 256 usando el método de división larga.
Paso 1. Divide el número en pares comenzando desde un lugar. Por ejemplo, pares comenzando desde un lugar:= 2 , 56

Paso 2. Después de dividir los dígitos en pares, comience desde el par o dígito más a la izquierda. El mayor número cuyo cuadrado es justo menor o igual que el primer par o dígito se toma como divisor y también como cociente. En el ejemplo anterior, el número más grande cuyo cuadrado es justo menor que 2 es 1. Entonces, el divisor es 1 y el cociente también es 1.

Paso 3. Resta el cuadrado del divisor del primer par o dígito y baja el siguiente par a la derecha del recordatorio para obtener el nuevo dividendo. En el ejemplo anterior, 2 – 1 = 1, bajamos el siguiente par, es decir, 56, y el nuevo dividendo se convierte en 156.


Paso 4. Ahora, el nuevo divisor se obtiene sumando el divisor anterior y el dígito anterior del cociente y concatenándolo con un dígito adecuado que también se toma como el siguiente dígito del cociente, elegido de tal manera que el producto del nuevo divisor y este nuevo dígito en el cociente es igual o apenas menor que el nuevo dividendo. En el ejemplo anterior, el divisor anterior es 1 y el dígito del cociente anterior es 1 y su suma da 2, que es el nuevo divisor. Ahora, tenemos que elegir un dígito para que el producto del nuevo divisor y el nuevo dígito en el cociente sea igual o menor que el nuevo dividendo, es decir, 26 es el nuevo divisor y 6 en el nuevo dígito que se concatena con el anterior. cociente. Ahora, el cociente actual es 16.

Paso 5. Repita los pasos 2, 3 y 4 hasta que se hayan tomado todos los pares. Ahora, el cociente resultante es la raíz cuadrada del número dado. En el ejemplo anterior, se tomaron todos los pares y, por lo tanto, la raíz cuadrada del número 256 es 16.
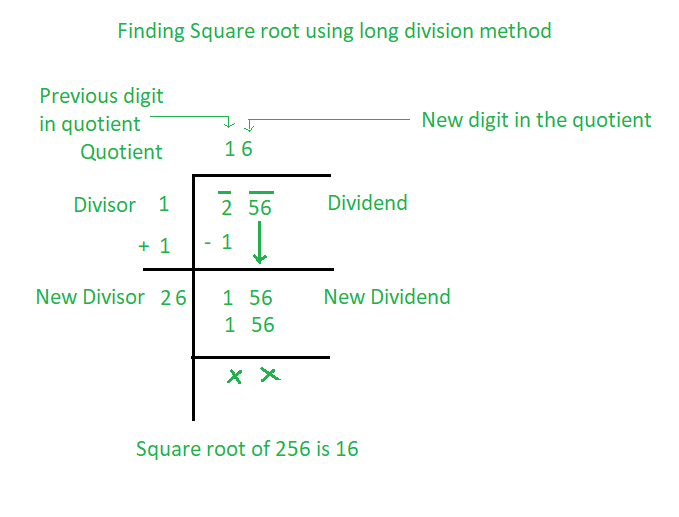
Tabla para el cuadrado y la raíz cuadrada de los diez primeros números naturales
| Número | Cuadrado | Raíz cuadrada |
|---|---|---|
| 1 | 1 | √1 = 1 |
| 2 | 4 | √2 = 1.414 |
| 3 | 9 | √3 = 1.732 |
| 4 | dieciséis | √4 = 2 |
| 5 | 25 | √5 = 2.236 |
| 6 | 36 | √6 = 2.4494 |
| 7 | 49 | √7 = 2.645 |
| 8 | 64 | √8 = 2.828 |
| 9 | 81 | √9 = 3 |
| 10 | 100 | √10 = 3.162 |
Fórmula de raíz cuadrada
La raíz cuadrada de un número tiene el exponente 1/2. La fórmula de la raíz cuadrada se usa para encontrar la raíz cuadrada de un número.
Fórmula de la raíz cuadrada: √x = x 1/2
| Fórmula de raíz cuadrada |
|---|
| √x = x 1/2 |
| √x. √x = x |
| x√y. x√y = x 2 y |
| √(x × y) = √x × √y |
| √(x / y) = √x / √y |
| x / √y = (x / √y) × ( √y / √y) = (x . √y)/y |
| X. √y ± z. √y = (x ± z) √y |
|
x / (y + z. √p) = [x / (y + z√p)]×[(y – z√p)/ (y – z√p)] = [x(y – z√p)]/[y 2 – z 2 p] Racionalizar el denominador multiplicando por [(y – z√p)/ (y – z√p)] |
|
x / (y – z. √p) = [x / (y – z√p)]×[(y + z√p)/ (y + z√p)] = [x(y + z√p)]/[y 2 – z 2 p] Racionalizar el denominador multiplicando por [(y + z√p)/ (y + z√p)] |
Problemas de muestra
Pregunta 1: Encuentra la suma: 5√3 + 6√12
Solución:
5√3 + 6√12 = 5√3 + 6(√(4 × 3)
= 5√3 + 6 × √4 × √3
= 5√3 + 6 ×2√3
= 5√3 + 12√3
= 17√3
Pregunta 2: Evaluar: √64 – √25
Solución:
√64 – √25 = √(8 × 8) – √(5 × 5 )
= 8 – 5 = 3
Pregunta 3: Evalúa: √63 / √28
Solución:
√63 / √28 = √(7 × 9 )/ √(7 × 4 )
= √[(7 × 9 )/ (7 × 4 )]
= √(9 /4)
= √9 / √4
= 3/2
Pregunta 4: Evaluar: 5 /√15
Solución:
5 /√15 = (5 /√15)×(√15 /√15 )
= (5√15)/15
= (√15)/3
Pregunta 5: Evalúa: 4 / (5 + √6)
Solución:
4 / (5 + √6) = [4 / (5 + √6)] × [(5 – √6) / (5 – √6)]
El paso anterior es racionalizar el denominador multiplicando por [(5 – √6) / (5 – √6)]
= [4×(5 – √6)] / [(5 + √6)× (5 – √6)]
= [4×(5 – √6)] / [5 2 – (√6) 2 ]
= (20 – 4√6) / (25 – (√6 × √6)]
= (20 – 4√6) / (25 – 6)
= (20 – 4√6) / 19
Pregunta 6: Evaluar: 7 / (8 – √10)
Solución:
7 / (8 – √10) = [7 / (8 – √10)] × [(8 + √10) / (8 + √10)]
El paso anterior es racionalizar el denominador multiplicando por [(8 + √10) / (8 + √10)]
= [7×(8 + √10)] / [(8 – √10) × (8 + √10)]
= [7×(8 + √10)] / [8 2 – (√10) 2 ]
= (56 + 7√10) / (64 – (√10 × √10)]
= (56 + 7√10) / (64 – 10)
= (56 + 7√10) / 54
Pregunta 7: Evalúa: (2 +√5) / (4 – √2)
Solución:
(2 +√5) / (4 – √2) = [(2 +√5) / (4 – √2)] × [(4 + √2) / (4 + √2)]
El paso anterior es racionalizar el denominador multiplicando por [(4 + √2) / (4 + √2)]
= [(2 +√5) × (4 + √2)] / [(4 – √2) × (4 + √2)]
= [(2 +√5) × (4 + √2)] / [4 2 – (√2) 2 ]
= [8 + 2√2 + 4√5 + (√5 × √2)] / [16 – (√2 × √2)]
= [8 + 2√2 + 4√5 + √(5×2)] / [16 – 2]
= [8 + 2√2 + 4√5 + √10] / 14
Publicación traducida automáticamente
Artículo escrito por aayushi2402 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA