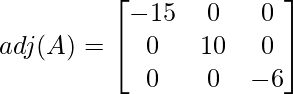¿Cómo encontrar la diagonal de una array?

El matemático británico Arthur Cayley fue la primera persona en desarrollar el aspecto algebraico de la array. Después de eso, Psychiat Heisenberg usó arrays como herramienta para explicar su famoso principio cuántico. El estudio de las arrays se originó en la resolución de diferentes tipos de problemas lineales simples y complejos, los cuales son engorrosos de resolver sin arrays. Una array rectangular de mn números en forma de m líneas horizontales llamadas filas y n líneas verticales llamadas columnas se llama array de orden mx n. Esta array está encerrada entre [ ] o ( ) o || || . Cada número de la array mxn se conoce como el elemento de la array. Una array generalmente se denota con caracteres alfabéticos en mayúscula, y su elemento se denota con caracteres alfabéticos pequeños con el sufijo ij, que indica el número de fila y columna, es decir, aij, se denominan elementos de la array A.

$A= \begin{bmatrix} 2 & 6 & 4 \\ 1 & 2 & 3 \\ 8 &9 &7 \end{bmatrix}$

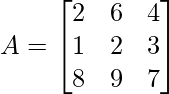
Los elementos de la array pueden ser cantidades escalares o vectoriales.
Una array es solo un arreglo de números; no tiene un valor definido. es decir, [5] ≠ 5.

Algunos términos importantes relacionados con la array

Elementos de una Array: Cada uno de los números M, N de la Array se denomina elemento o entrada de la Array.
Notación de una array: una array generalmente se representa mediante los símbolos [a _ij ] o (a _ij ) o ||a _ij ||. Una array se denota con una sola letra mayúscula, como A, B, C, etc.
Orden de una array: Se dice que una array que tiene m filas y n columnas es una array de orden mx n.

Elementos diagonales de una array

Un elemento aij de una array A = [a _ij ] es un elemento diagonal de la array si i = j, como cuando los sufijos de filas y columnas son iguales. Así, a ₁₁ , a ₂₂ , a ₃₃ , a ₄₄ , … etc. son elementos diagonales de la array A = [a _ij ].

Diagonal principal de una array

La diagonal principal también se conoce como diagonal principal. La diagonal de una array cuadrada que va desde las entidades superiores izquierdas hasta las entidades inferiores derechas es la diagonal principal de una array.

$A = \begin{bmatrix} a_{11} & 0 & 0 \\ 0 & a_{22} & 0 \\ 0 & 0 & a_{33} \end{bmatrix}$

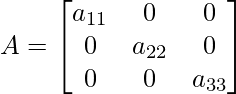
Aquí, los elementos de la Diagonal Principal son distintos de cero.

Contradiagonal

También se llama antidiagonal de una array. La diagonal de una array cuadrada que se extiende desde las entidades superiores derechas hasta las entidades inferiores izquierdas se denomina contradiagonal de una array.

$B = \begin{bmatrix} 0 & 0 & b_{13} \\ 0 & b_{22} & 0 \\ b_{31} & 0 & 0 \end{bmatrix}$

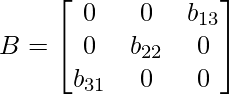
Aquí, los elementos de la contradiagonal son distintos de cero.

Nota: Arriba, consideramos ejemplos en diagonal principal y contradiagonal. Los elementos de la array distintos a la diagonal se consideran como ceros para una mejor aclaración.

Ejemplos de problemas

Pregunta 1: Averigüe el elemento diagonal de la siguiente array.

$A = \begin{bmatrix} 9 & 0 & 25 \\ 0 & 8 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

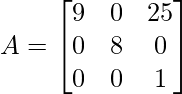
Solución:

Como sabemos, encontrar la diagonal de una array o elementos diagonales no es una tarea pesada; es solo una práctica básica de arrays. Si alguien nos dijo que encontráramos el elemento diagonal, como resultado solo encontramos la diagonal principal. que va desde las entidades de la parte superior izquierda a las entidades de la parte inferior derecha

Elemento diagonal de array,

un ₁₁ = 9, un ₂₂ = 8, un ₃₃ = 1

Pregunta 2: Encuentre la traza de la array A, dada a continuación.

$A = \begin{bmatrix} 1 & 2 & 3 \\ 0 & 2 & 0 \\ 5 & 0 & 5 \end{bmatrix}$

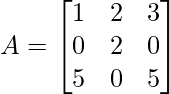
Solución:

Rastro de array: en realidad es la suma del elemento diagonal principal.

tr(A) = un ₁₁ + un ₂₂ + un _33;

Entonces, después de la observación de la array

Podemos decir, un ₁₁ = 1, un ₂₂ = 2, un ₃₃ = 5

tr(a) = 1 + 2 + 5 = 8

Pregunta 3: Encuentra la inversa de la array diagonal:

$A = \begin{bmatrix} 2 & 0 & 0 \\ 0 & -3 & 0 \\ 0 & 0 & 5 \end{bmatrix}$

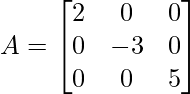
Solución:

Determinante de la array de A,

|A| = -30

Adjunto de la array A,

$adj(A) = \begin{bmatrix} -15 & 0 & 0 \\ 0 & 10 & 0 \\ 0 & 0 & -6 \end{bmatrix}$

Sabemos que la inversa de la array A es: A ^-1 = \frac{adj(A)}{|A|}

$A-1 = \begin{bmatrix} \frac{1}{2} & 0 &0 \\ 0 & \frac{-1}{3}& 0 \\ 0 & 0 & \frac{1}{5} \end{bmatrix}$

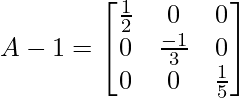
Pregunta 4: Encuentre el valor de un ₁₁ + un ₂₃ – un ₂₂ + un ₃₁ de la siguiente array.

$A = \begin{bmatrix} 8 & 2 & 5 \\ 0 & 2 & 9 \\ 5 & 6 & 5 \end{bmatrix}$

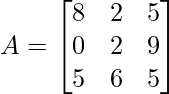
Solución:

Conocemos la sintaxis matricial estándar.

$A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21}& a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$

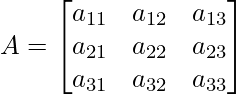
Al compararlo con nuestra array podemos decir,

un ₁₁ = 8, un ₂₃ = 9, un ₂₂ = 2, un ₃₁ = 5

Resultado requerido: a ₁₁ + a ₂₃ – a ₂₂ + a ₃₁ = 8 + 9 – 2 – 5 = 10

Pregunta 5: encuentre el producto del elemento diagonal de la siguiente array:

$A = \begin{bmatrix} 2 & 5 & 6 \\ 1 & 4 & 8 \\ 4 & 2 & 1 \end{bmatrix}$

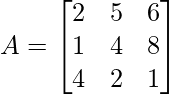
Solución:

Los elementos diagonales de la array anterior son 2, 4 y 1, respectivamente

Producto de diagonal: 2 × 4 × 1 = 8

Pregunta 6: Encuentre el determinante de la array dada a continuación:

$A = \begin{bmatrix} 5 & 2 & 6 \\ 4 & 1 & 8 \\ 2 & 4 & 1 \end{bmatrix}$

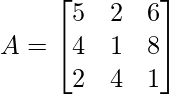
Solución:

Determinante de la array A,

|A| = 5 (1 – 32) – 2 (16 – 4) + 6 (16 – 2)

|A| = 5(-31) – 2(12) + 6(14)

|A| = -155 – 24 + 84 = -95

Pregunta 7: Encuentra la suma de la contradiagonal de la array, el elemento común del principio y la contradiagonal:

$A = \begin{bmatrix} 8 & 2 & 5 \\ 0 & 2 & 9 \\ 5 & 6 & 5 \end{bmatrix}$

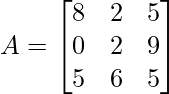
Solución:

Sabemos que la array cuadrada que va desde las entidades superiores derechas hasta las entidades inferiores izquierdas son contradiagonales de array.

Entonces, los elementos contradiagonales son

un ₁₃ = 5 un ₂₂ = 2 un ₃₁ = 5

El elemento común de la diagonal principal y la contradiagonal es 2.

Publicación traducida automáticamente

Artículo escrito por uditsharma333jj y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Algunos términos importantes relacionados con la array

Elementos diagonales de una array

Ejemplos de problemas

Deja una respuesta Cancelar la respuesta