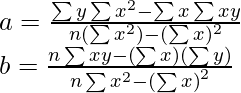Fórmula de regresión lineal

La regresión lineal se define como una técnica de datos que determina la relación entre dos variables aplicando una ecuación lineal a los datos dados. Aquí, se supone que una variable es independiente, mientras que la otra se supone que es dependiente. Se usa con la ayuda de una ecuación de regresión lineal, que es similar a la forma pendiente-intersección. Para medir la fuerza de la relación entre dos variables, usamos un coeficiente de correlación que tiene un rango de valores de -1 a +1. La pendiente de la línea de regresión se calcula poniendo la variable independiente igual a cero en la ecuación y luego resolviendo la variable dependiente.

Fórmula de regresión lineal

y = a + bx

Dónde,

y es la variable dependiente que se encuentra a lo largo del eje y,

a es el intercepto en y,

b es la pendiente de la línea de regresión,

x es la variable independiente que se encuentra a lo largo del eje x,

El valor del intercepto, a, y la pendiente de la línea, b, se evalúan utilizando las fórmulas que se dan a continuación:

$\begin{array}{l}\large a=\frac{\sum y \sum x^{2} - \sum x \sum xy} {n(\sum x^{2}) - (\sum x)^{2}}\end{array}\\ \begin{array}{l}\large b=\frac{n\sum xy-\left(\sum x\right)\left(\sum y\right)}{n\sum x^{2}-\left(\sum x\right)^{2}}\end{array}$

Dónde,

x denota los valores del conjunto de datos independiente,

y denota los valores del conjunto de datos dependientes.

Problemas de muestra

Problema 1: Encuentra la ecuación de regresión lineal para los datos dados:

X	y
3	8
9	6
5	4
3	2

Solución:

Calcular el valor de la intersección y la pendiente.

X

y

x2 ^_

xy

3

9

9

27

5

3

25

15

8

6

64

48

4

2

dieciséis

8

∑x = 20

∑y = 20

∑x2 ⁼ 114

∑xy = 98

Usando la fórmula que obtenemos,

$\begin{array}{l}\large a=\frac{\sum y \sum x^{2} - \sum x \sum xy} {n(\sum x^{2}) - (\sum x)^{2}}\end{array}\\$

= (20 (114) – 20 (98)) / (4 (114) – 400)

= 320/56

= 5,71

$\begin{array}{l}\large b=\frac{n\sum xy-\left(\sum x\right)\left(\sum y\right)}{n\sum x^{2}-\left(\sum x\right)^{2}}\end{array}$

= (4 (98) – 20 (20)) / (4 (114) – 400)

= -8/56

= -0.14

Entonces, la ecuación de regresión lineal es 5.71 – 0.14 x.

Problema 2: Encuentra la ecuación de regresión lineal para los datos dados:

X	y
4	6
7	5
3	8
1	3

Solución:

Calcular el valor de la intersección y la pendiente.

X

y

x2 ^_

xy

4

6

dieciséis

24

7

5

49

35

3

8

9

24

1

3

1

3

∑x = 15

∑y = 22

∑x2 ⁼ 75

∑xy = 134

Usando la fórmula que obtenemos,

$\begin{array}{l}\large a=\frac{\sum y \sum x^{2} - \sum x \sum xy} {n(\sum x^{2}) - (\sum x)^{2}}\end{array}\\$

= (15 (75) – 15 (134)) / (4 (75) – 225)

= -885/75

= -11,8

$\begin{array}{l}\large b=\frac{n\sum xy-\left(\sum x\right)\left(\sum y\right)}{n\sum x^{2}-\left(\sum x\right)^{2}}\end{array}$

= (4 (134) – 15 (22)) / (4 (75) – 225)

= -206/75

= -0.14

Entonces, la ecuación de regresión lineal es, -11.8 – 2.74 x.

Problema 3: encuentre la intersección de la línea de regresión lineal si ∑x = 25, ∑y = 20, ∑x ² = 90, ∑xy = 150 y n = 5.

Solución:

Usando la fórmula que obtenemos,

$\begin{array}{l}\large a=\frac{\sum y \sum x^{2} - \sum x \sum xy} {n(\sum x^{2}) - (\sum x)^{2}}\end{array}\\$

= (20 (90) – 25 (150)) / (5 (90) – 625)

= -1950/-175

= 11,14

Problema 4: encuentre la intersección de la línea de regresión lineal si ∑x = 30, ∑y = 27, ∑x ² = 110, ∑xy = 190 y n = 4.

Solución:

Usando la fórmula que obtenemos,

$\begin{array}{l}\large a=\frac{\sum y \sum x^{2} - \sum x \sum xy} {n(\sum x^{2}) - (\sum x)^{2}}\end{array}\\$

= (27 (110) – 25 (190)) / (5 (110) – 900)

= -1780/-350

= 5,08

Problema 5: Encuentra la pendiente de la línea de regresión lineal si ∑x = 10, ∑y = 16, ∑x ² = 60, ∑xy = 120 y n = 4.

Solución:

Usando la fórmula que obtenemos,

$\begin{array}{l}\large b=\frac{n\sum xy-\left(\sum x\right)\left(\sum y\right)}{n\sum x^{2}-\left(\sum x\right)^{2}}\end{array}$

= (4 (120) – 10 (16)) / (4 (60) – 100)

= 320/140

= 2,28

Problema 6: Encuentra la pendiente de la línea de regresión lineal si ∑x = 40, ∑y = 32, ∑x ² = 130, ∑xy = 210 y n = 4.

Solución:

Usando la fórmula que obtenemos,

$\begin{array}{l}\large b=\frac{n\sum xy-\left(\sum x\right)\left(\sum y\right)}{n\sum x^{2}-\left(\sum x\right)^{2}}\end{array}$

= (4 (210) – 40 (32)) / (4 (130) – 1600)

= -440/-1080

= 0,404

Problema 7. Encuentra la pendiente de la línea de regresión lineal si ∑x = 50, ∑y = 44, ∑x ² = 150, ∑xy = 230 y n = 4.

Solución:

Usando la fórmula que obtenemos,

$\begin{array}{l}\large a=\frac{\sum y \sum x^{2} - \sum x \sum xy} {n(\sum x^{2}) - (\sum x)^{2}}\end{array}\\$

= (44 (150) – 50 (230)) / (4 (150) – 2500)

= -4900/-1900

= 2,57

$\begin{array}{l}\large b=\frac{n\sum xy-\left(\sum x\right)\left(\sum y\right)}{n\sum x^{2}-\left(\sum x\right)^{2}}\end{array}$

= (4 (230) – 50 (44)) / (4 (150) – 2500)

= -1280/-1900

= 0,67

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Fórmula de regresión lineal

Problemas de muestra

Deja una respuesta Cancelar la respuesta