La fórmula de Euler ocupa un lugar destacado en el campo de las matemáticas. Ayuda a establecer el vínculo esencial entre funciones trigonométricas y funciones exponenciales complejas. Es una fórmula crucial utilizada para resolver funciones exponenciales complicadas. También se conoce como identidad de Euler. Tiene muchas aplicaciones en análisis complejo y se usa para encontrar el número de vértices y caras de un poliedro.
Fórmula para análisis complejo
La fórmula de análisis complejo nos proporciona una forma de expresar la potencia imaginaria de las funciones exponenciales en forma de razones trigonométricas. Su fórmula se puede relacionar con un plano complejo, donde una función unitaria compleja e ix traza un círculo unitario, tal que x es un número real medido en radianes.
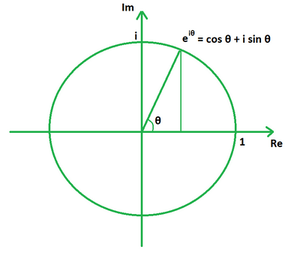
e ix = cos x + i sen x
dónde,
x es un número real,
e es la base del logaritmo,
sen x y cos x son las funciones trigonométricas,
i es la parte imaginaria.
La expresión cos x + i sen x también se conoce como forma polar de un número complejo.
Derivación
Considere la serie de expansión de la función exponencial e x .
e x = 1 + x + x 2 /2! + x 3 /3! + x 4 /4! + …….. + ∞
Sustituyendo x como ix obtenemos,
e ix = 1 + ix + (ix) 2 /2! + (ix) 3/3 ! + (ix) 4/4 ! + …….. + ∞
Usando la propiedad i 2 = -1 obtenemos,
= 1 + ix – x 2 /2! – ix 3 /3! + x 4 /4! + …….. + ∞
= (1 – x 2 /2! + x 4 /4! – …….. + ∞) + i (x – x 3 /3! + x 5 /5! – …….. + ∞)
Usando la propiedad de expansión en serie de las funciones seno y coseno obtenemos,
= cos x + i sen x
De aquí se deriva la fórmula de Euler para el análisis complejo.
Fórmula para poliedro
La fórmula poliédrica de Euler establece que el número de caras, vértices y aristas de cada poliedro que no se corta a sí mismo están conectados de cierta manera. Su fórmula dice que el número de vértices y caras de un poliedro combinado es dos más que su número de aristas.
F + V – E = 2
dónde,
F es el número de caras,
V el número de vértices,
E el número de aristas.
Derivación
La fórmula de Euler se puede probar para cinco sólidos platónicos: el cubo, el tetraedro, el octaedro, el dodecaedro y el icosaedro.
Sólidos
Número de caras (F)
Número de vértices (V)
Número de aristas (E)
F + V-E
Cubo
4
4
6
2
tetraedro
6
8
12
2
Octaedro
8
6
12
2
Dodecaedro
12
20
30
2
icosaedro
20
12
30
2
Problemas de muestra
Problema 1. Expresar e iπ/2 en forma general usando la fórmula de Euler.
Solución:
Tenemos,
x = π/2
Usando la fórmula que obtenemos,
e ix = cos x + i sen x
= cos π/2 + i sen π/2
= 0 + yo (1)
= 0 + yo
Problema 2. Expresar e 6i en forma general usando la fórmula de Euler.
Solución:
Tenemos,
x = 6
Usando la fórmula que obtenemos,
e ix = cos x + i sen x
= cos 6 + yo seno 6
= 0,96 + yo (-0,279)
= 0,96 – 0,279i
Problema 3. Expresar e 10i en forma general usando la fórmula de Euler.
Solución:
Tenemos,
X = 10
Usando la fórmula que obtenemos,
e ix = cos x + i sen x
= cos 10 + yo seno 10
= -0,83 + yo (-0,544)
= -0.83 – 0.544i
Problema 4. Expresar e iπ/3 en forma general usando la fórmula de Euler.
Solución:
Tenemos,
x = π/3
Usando la fórmula que obtenemos,
e ix = cos x + i sen x
= cos π/3 + i sen π/3
= 0,5 + yo (0,86)
= 0,5 + 0,86i
Problema 5. Verificar la fórmula de Euler para un prisma triangular.
Solución:
Tenemos un prisma triangular. Se sabe que,
Número de caras (F) = 5
Número de vértices (V) = 6
Número de aristas (E) = 9
Usando la fórmula que tenemos,
F + V – mi = 5 + 6 – 9
= 11 – 9
= 2
Como el valor de F + V − E es 2, se verifica la fórmula de Euler.
Problema 6. Verificar la fórmula de Euler para una pirámide cuadrada.
Solución:
Tenemos una pirámide cuadrada. Se sabe que,
Número de caras (F) = 5
Número de vértices (V) = 5
Número de aristas (E) = 8
Usando la fórmula que tenemos,
F + V – mi = 5 + 5 – 8
= 10 – 8
= 2
Como el valor de F + V − E es 2, se verifica la fórmula de Euler.
Problema 7. Calcular el número de vértices de un poliedro si el número de caras es 20 y las aristas 30.
Solución:
Tenemos,
F = 20
mi = 30
Usando la fórmula que obtenemos,
F + V – mi = 2
=> V = mi + 2 – F
= 30 + 2 – 20
= 32 – 20
= 12
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA