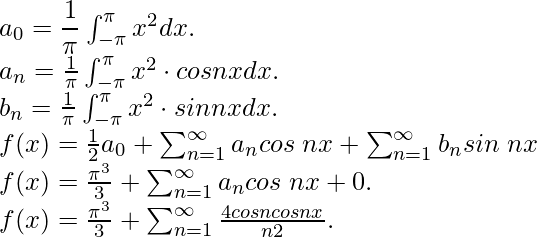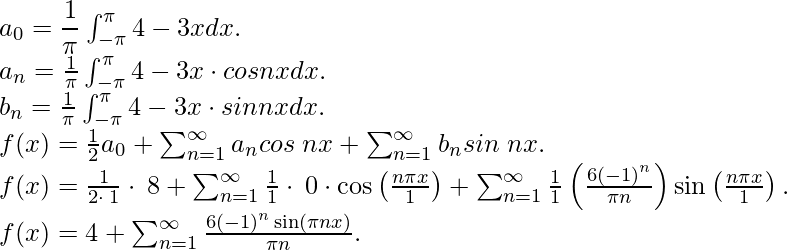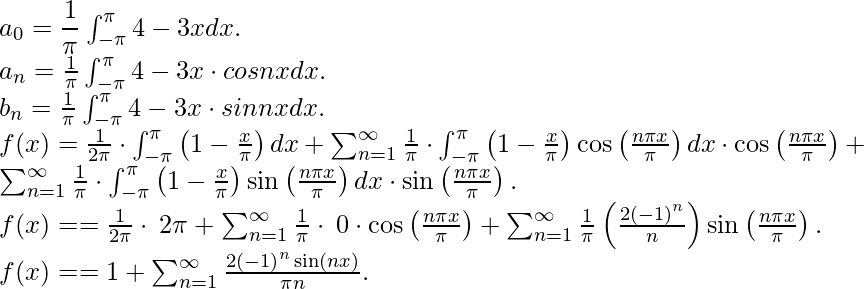Fórmula de la serie de Fourier

Una serie de Fourier es una suma de ondas seno y coseno que representa una función periódica. Cada onda en la suma, o armónico, tiene una frecuencia que es un múltiplo entero de la frecuencia fundamental de la función periódica. El análisis armónico se puede utilizar para identificar la fase y la amplitud de cada armónico. Una serie de Fourier puede tener un número ilimitado de armónicos. Sumando algunos, pero no todos, los armónicos en la serie de Fourier de una función, se obtiene una aproximación a esa función. Por ejemplo, se puede aproximar una onda cuadrada utilizando los primeros armónicos de la serie de Fourier.

Series de Fourier

Como se vio anteriormente, las funciones periódicas a menudo aparecen en problemas de matemáticas superiores. Una forma de lidiar con estos problemas es representarlos en términos de funciones periódicas básicas, que tienen un rango pequeño y pueden tener un dominio de todos los números reales, como el seno y el coseno; esto nos lleva a la serie de Fourier (FS). La serie de Fourier es una herramienta particularmente útil para tratar situaciones que involucran ecuaciones diferenciales parciales.

Supongamos que nos dan una función periódica f(x). Ahora como la función original es periódica por lo tanto,

c ₁ f ₁ (x) + … + c _norte f _norte (x)

Luego considere la serie infinita,

$\begin{array}{l}\frac{1}{2} a_{o}+ \sum_{ n=1}^{\infty}a_{n}\;cos\frac{n\pi x}{L}+b_{n}\; sin\frac{n\pi x}{L}\end{array}$ ⇢ (1)

Consta de funciones periódicas 2L converge para todo x, entonces la función a la que converge será periódica de periodo 2L. Ahora, como se vio arriba, necesitamos representar la función f(x) de tal manera que la función periódica f(x) sea reemplazada por funciones como seno y coseno. Para esto la serie de Fourier está dada por,

$\large f(x)=\frac{1}{2}a_{0}+\sum_{n=1}^{\infty}a_{n}cos\;nx+\sum_{n=1}^{\infty}b_{n}sin\;nx$

Aquí,

$\frac{1}{\pi} \int_{- \pi}^{\pi} f(x) dx$

$\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)cos\;nx\;dx$ .

$\frac{1}{\pi} \int_{-\pi}^{\pi}f(x)sin\;nx\;dx$ .

n = 1,2,3….

Forma general de la Serie de Fourier

Para cualquier función f(x) con periodo 2L, la serie de Fourier se da como,

$f(x)=\begin{array}{l}\frac{1}{2} a_{o}+ \sum_{ n=1}^{\infty}a_{n}\;cos\frac{n\pi x}{L}+b_{n}\; sin\frac{n\pi x}{L}\end{array}$ .

Forma exponencial de la serie de Fourier

De la ecuación anterior,

$f(x)=\begin{array}{l}\frac{1}{2} a_{o}+ \sum_{ n=1}^{\infty}a_{n}\;cos\frac{n\pi x}{L}+b_{n}\; sin\frac{n\pi x}{L}\end{array}$ .

Ahora, de acuerdo con la fórmula de Euler,

e ^iθ = cosθ +isinθ

Usando esto

f(x) = $\sum_{n=-\infty}^{\infty}$ C _norte mi ^inx .

Aquí Cn se llama coeficiente de descomposición y se calcula como,

$C_n = \frac{1}{2T} \int_{-T}^{T}e^{{-in}\frac{\pi t}{T} }f(t)$ .

Condiciones para la serie de Fourier

Supongamos que una función f(x) tiene un periodo de 2π y es integrable en un periodo [-π, π]. Ahora hay dos condiciones.

La función f(x) con periodo 2π es absolutamente integrable en [-π, π] por lo que la siguiente integral de Dirichlet de esta función es finita:
$\int\limits_{ - \pi }^\pi {\left| {f\left( x \right)} \right|dx} \lt \infty ;$

La siguiente condición es que la función sea de un solo valor, continua por partes (debe tener un número finito de discontinuidades de salto) y monótona por partes (debe tener un número finito de máximos y mínimos).

Si se cumplen las condiciones 1 y 2, la serie de Fourier para la función existe y converge a la función dada. Esto significa que la suma de la serie de Fourier de cualquier función dada converge para dar la misma función. Esta es la definición básica de la expansión de la serie de Fourier. Antes de comprender mejor el concepto de la serie de Fourier, primero debemos comprender el concepto de funciones pares e impares y funciones periódicas.

Función impar: Supongamos que nos dan una función y = f(x).

Ahora si,

f(-x) = -f(x) = -y

entonces se dice que la función es impar.

La función es de naturaleza impar y simétrica con respecto al origen.

Función par : Nuevamente considere una función f(x) = y.

Si f(-x) = f(x) = y

Entonces la función es uniforme en la naturaleza.

Esta es una función par cuya gráfica es simétrica a lo largo del eje y.

Funciones periódicas: Sea una función f(x) periódica con un intervalo λ. Ahora considere un elemento x como parte del dominio de esta función. Esto significa que,

f(x) = f(x + λ).

La gráfica de la función tanx es un ejemplo de una función periódica.

Por lo tanto, las funciones periódicas son aquellas funciones que se repiten en un intervalo de valores (λ como se muestra arriba). El valor positivo más pequeño posible de λ se llama período de esta función.

Series de Fourier

Ejemplos de problemas

Pregunta 1: Encuentra la expansión en serie de Fourier de la función f(x) = e ^x , dentro de los límites [– π, π].

Solución :

Usando la expansión de la serie de Fourier.

$a_0 = \dfrac{1}{2\pi}\int_{- \pi}^{\pi}e^x dx \\= \dfrac{e^\pi - e^{-\pi}}{2\pi}$ .

$a_n = \dfrac{1}{\pi}\int_{- \pi}^{\pi}e^x cos (nx) dx \\= \dfrac{1}{\pi}\dfrac{e^x}{1+n^2}[\cos(nx)+ n\sin(nx)]_{-\pi}^{\pi}\\= \dfrac{1}{\pi(1+n^2)}[e^\pi(-1)^n)-e^{-\pi}(-1)^n)]$ .

$b_n = \dfrac{1}{\pi}\int e^x sin(nx) dx \\= \dfrac{e^x}{\pi (1+n^2)}[\sin(nx)- n \cos(nx)]_{-\pi}^{\pi}\\= \dfrac{1}{\pi (1+n^2)}[e^\pi(-n(-1)^n) - e^{-\pi}(-n)(-1)^n]$ .

La serie de Fourier para esta función se da como,

$\dfrac{e^\pi -e^{-\pi}}{2\pi} + \sum_{n=1}^{\infty}\dfrac{(-1)^n(e^\pi - e^{-\pi})}{\pi(1+n^2)}[cos nx -n sin nx]$ .

Pregunta 2: Encuentra la expansión en serie de Fourier de la función f(x) = x , dentro de los límites [– 1, 1].

Solución:

De la expansión de la serie de Fourier. Aquí,

$A_{0}=\frac{1}{2 } \cdot \int_{-1}^{1} x d x$ .

$A_{n}=\frac{1}{1} \cdot \int_{-1}^{1} x \cos \left(\frac{n \pi x}{1}\right) d x, \quad n>0$ .

$B_{n}=\frac{1}{1} \cdot \int_{-1}^{1} x \sin \left(\frac{n \pi x}{1}\right) d x, \quad n>0$ .

$f(x)=A_{0}+\sum_{n=1}^{\infty} A_{n} \cdot \cos \left(\frac{n \pi x}{L}\right)+\sum_{n=1}^{\infty} B_{n} \cdot \sin \left(\frac{n \pi x}{L}\right)$ .

$\mathrm{f}(\mathrm{x})=\frac{1}{2 \cdot 1} \cdot \int_{-1}^{1}\left(x\right) d x+\sum_{n=1}^{\infty} \frac{1}{1} \cdot \int_{-1}^{1}\left(x\right) \cos \left(\frac{n \pi x}{1}\right) d x \cdot \cos \left(\frac{n \pi x}{1}\right)+\sum_{n=1}^{\infty} \frac{1}{1} \cdot \int_{-1}^{1}\left(x\right) \sin \left(\frac{n \pi x}{1}\right) d x \cdot \sin \left(\frac{n \pi x}{1}\right)$ .

Al resolver las integrales obtenemos funciones pares y una función impar. Por lo tanto,

$f(x) = \sum _{n=1}^{\infty \:}-\frac{2\left(-1\right)^n\sin \left(\pi nx\right)}{\pi n}$ .

Pregunta 3: Supongamos que una función f(x) = tanx encuentra su expansión de Fourier dentro de los límites [-π, π].

Solución:

$a_0 = \dfrac{1}{\pi}\int_{- \pi}^{\pi} tanx dx$

$a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} tanx cosnxdx$

$b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} tanx sinnxdx$

$\large f(x)=\frac{1}{2}a_{0}+\sum_{n=1}^{\infty}a_{n}cos\;nx+\sum_{n=1}^{\infty}b_{n}sin\;nx$

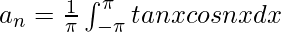
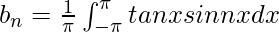
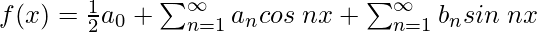
Ahora no se puede encontrar la integral de tanx⋅sinnx y tanx⋅cosnx.

Por lo tanto, la serie de Fourier para esta función f(x) = tanx no está definida.

Pregunta 4: Encuentra la serie de Fourier de la función f(x) = 1 para límites [– π, π] .

Solución:

Comparando con la expansión general de la serie de Fourier obtenemos,

$a_0 = \dfrac{1}{\pi}\int_{- \pi}^{\pi}1 dx$

$a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} 1 \cdot cosnxdx$

$b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} 1 \cdot sinnxdx .\\ \large f(x)=\frac{1}{2}a_{0}+\sum_{n=1}^{\infty}a_{n}cos\;nx+\sum_{n=1}^{\infty}b_{n}sin\;nx$

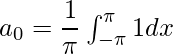
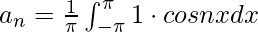
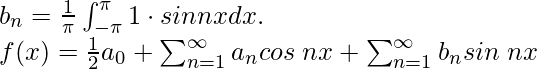
f(x) = π + 0 + 0

f(x) = π

Pregunta 5: Considere una función f(x) = x ² para los límites [– π, π]. Encuentre su expansión en serie de Fourier.

Solución:

Comparando con la expansión general de la serie de Fourier obtenemos,

$a_0 = \dfrac{1}{\pi}\int_{- \pi}^{\pi}x^2 dx . \\ a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} x^2 \cdot cosnxdx . \\ b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} x^2 \cdot sinnxdx . \\ \large f(x)=\frac{1}{2}a_{0}+\sum_{n=1}^{\infty}a_{n}cos\;nx+\sum_{n=1}^{\infty}b_{n}sin\;nx \\ f(x) = \frac{{\pi}^{3}}{3} + \sum_{n=1}^{\infty}a_{n}cos\;nx +0 .\\ f(x) = \frac{{\pi}^{3}}{3} + \sum_{n=1}^{\infty} \frac{4πcosnπcosnx}{n2}.$

Pregunta 6: Encuentra el desarrollo en serie de Fourier de la función f(x) = 4-3x para los límites [– 1, 1].

Solución:

Comparando con la expansión general de la serie de Fourier obtenemos,

$a_0 = \dfrac{1}{\pi}\int_{- \pi}^{\pi}4-3x dx . \\ a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} 4-3x \cdot cosnxdx . \\ b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} 4 -3x\cdot sinnxdx .\\ \large f(x)=\frac{1}{2}a_{0}+\sum_{n=1}^{\infty}a_{n}cos\;nx+\sum_{n=1}^{\infty}b_{n}sin\;nx .\\ f(x) =\frac{1}{2\cdot \:1}\cdot \:8+\sum _{n=1}^{\infty \:}\frac{1}{1}\cdot \:0\cdot \cos \left(\frac{n\pi x}{1}\right)+\sum _{n=1}^{\infty \:}\frac{1}{1}\left(\frac{6\left(-1\right)^n}{\pi n}\right)\sin \left(\frac{n\pi x}{1}\right).\\ f(x) = 4+\sum _{n=1}^{\infty \:}\frac{6\left(-1\right)^n\sin \left(\pi nx\right)}{\pi n} .$

Pregunta 7: Encuentra la expansión de la función $1- \frac{x}{\pi}$ . Para los límites [– π, π].

Solución:

Comparando con la expansión general de la serie de Fourier obtenemos,

$a_0 = \dfrac{1}{\pi}\int_{- \pi}^{\pi}4-3x dx .\\ a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} 4-3x \cdot cosnxdx .\\ b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} 4 -3x\cdot sinnxdx .\\ f(x) = \frac{1}{2\pi }\cdot \int _{-\pi }^{\pi }\left(1-\frac{x}{\pi }\right)dx+\sum _{n=1}^{\infty \:}\frac{1}{\pi }\cdot \int _{-\pi }^{\pi }\left(1-\frac{x}{\pi }\right)\cos \left(\frac{n\pi x}{\pi }\right)dx\cdot \cos \left(\frac{n\pi x}{\pi }\right)+\sum _{n=1}^{\infty \:}\frac{1}{\pi }\cdot \int _{-\pi }^{\pi }\left(1-\frac{x}{\pi }\right)\sin \left(\frac{n\pi x}{\pi }\right)dx\cdot \sin \left(\frac{n\pi x}{\pi }\right) .\\ f(x) = =\frac{1}{2\pi }\cdot \:2\pi +\sum _{n=1}^{\infty \:}\frac{1}{\pi }\cdot \:0\cdot \cos \left(\frac{n\pi x}{\pi }\right)+\sum _{n=1}^{\infty \:}\frac{1}{\pi }\left(\frac{2\left(-1\right)^n}{n}\right)\sin \left(\frac{n\pi x}{\pi }\right).\\ f(x) = =1+\sum _{n=1}^{\infty \:}\frac{2\left(-1\right)^n\sin \left(nx\right)}{\pi n} .$

Publicación traducida automáticamente

Artículo escrito por harmansahani100 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Series de Fourier

Condiciones para la serie de Fourier

Series de Fourier

Ejemplos de problemas

Deja una respuesta Cancelar la respuesta