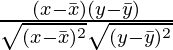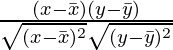¿Cómo calcular el Coeficiente de Correlación de Pearson?

El tema de la correlación viene bajo el concepto de estadísticas. Establece la relación entre dos variables. La fórmula del coeficiente de correlación encuentra el coeficiente de correlación que mide la dependencia de una variable con respecto a otra variable. El coeficiente de correlación se encuentra entre -1 y 1. Si el valor del coeficiente de correlación es negativo, la relación entre dos variables está inversamente relacionada. Si el valor es cero entonces no hay relación entre las dos variables. Si el valor del coeficiente de correlación es positivo, entonces una variable depende directamente de otra variable.

Coeficiente de correlación de Pearson

Hay muchos tipos de coeficientes de correlación. El más común y utilizado es el Coeficiente de Correlación de Pearson. El coeficiente de correlación de Pearson se representa con la letra ‘r’ y su fórmula para los datos de tamaño N viene dada por:

r = cov(x,y) _/ σx _σy

= $\frac{∑(x-\bar{x})(y-\bar{y})}{\sqrt{∑(x-\bar{x})^2}\sqrt{∑(y-\bar{ y})^2}}$

Donde cov representa covarianza

σ representa la desviación estándar

x ^– e y ^– representan medios

Problemas de muestra

Pregunta 1: encuentre la fórmula del coeficiente de correlación de Pearson para los datos dados

X	y
1	2
2	4
3	6

Solución:

X

y

$x-\bar{x}$

$y-\bar{y}$

$(x-\bar{x})^2$

$(y-\bar{y})^2$

$(x-\bar{x})(y-\bar{y})$

1

2

-1

-2

1

4

2

2

4

0

0

0

0

0

3

6

1

2

1

4

2

$\bar{x}$ =(1+2+3)/3

=6/3

$\bar{x}=2$

$\bar{y}$ =(2+4+6)/3

=12/3

$\bar{y}=4$

$∑(x-\bar{x})^2=2$

$∑(y-\bar{y})^2=8$

$∑(x-\bar{x})(y-\bar{y})=4$

Coeficiente de Pearson (r) = $\frac{∑(x-\bar{x})(y-\bar{y})}{\sqrt{∑(x-\bar{x})^2}\sqrt{∑(y-\bar{ y})^2}}$

= 4/(√2√8)

= 4/4

= 1

Por lo tanto, las dos variables x e y dependen directamente una de la otra.

Pregunta 2: encuentre la fórmula del coeficiente de correlación de Pearson para los datos dados

X	y
6	12
9	10
12	20

Solución:

X

y

$(x-\bar{x})$

$(y-\bar{y})$

$(x-\bar{x})^2$

$(y-\bar{y})^2$

$(x-\bar{x})(y-\bar{y})$

6

12

-3

-2

9

4

6

9

10

0

-4

0

dieciséis

0

12

20

3

6

9

36

18

$\bar{x}=$ (6+9+12)/3

=27/3

$\bar{x}=9$

$\bar{y}=$ (12+10+20)/3

=42/3

$\bar{y}=14$

$∑(y-\bar{y})^2=56$

$∑(x-\bar{x})(y-\bar{y})=24$

Coeficiente de Pearson (r) = $\frac{∑(x-\bar{x})(y-\bar{y})}{\sqrt{∑(x-\bar{x})^2}\sqrt{∑(y-\bar{ y})^2}}$

= 24/(√18√56)

= 24/(3√2 × 2√14)

= 4/2√7

= 2/√7

Coeficiente de Pearson = 0,75

Pregunta 3: encuentre la fórmula del coeficiente de correlación de Pearson para los datos dados

X	y
1	9
2	1
3	2
4	8

Solución:

X y $x-\bar{x}$ $y-\bar{y}$ $(x-\bar{x})^2$ $(y-\bar{y})^2$ $(x-\bar{x})(y-\bar{y})$

1 9 -1.5 4 2.25 dieciséis -6

2 1 -0.5 -4 0.25 dieciséis 2

3 2 0.5 -3 0.25 9 -1.5

4 8 1.5 3 2.25 9 4.5

$\bar{x}=$ (1+2+3+4)/4

=10/4

=2.5

$\bar{y}=$ (9+1+8+2)/4

=20/4

=5
$∑(x-\bar{x})^2=5$ $∑(y-\bar{y})^2=50$ $∑(x-\bar{x})(y-\bar{y})=-1$

= -1/(√5√50)

= -1/(5√10)

Coeficiente de Pearson = -0,63

El valor negativo del coeficiente de Pearson indica que 2 variables tienen menos dependencia entre ellas.

Pregunta 4: encuentre la fórmula del coeficiente de correlación de Pearson para los datos dados

X	10	5	20	7
y	2	9	10	1

Solución:

X

y

$x-\bar{x}$

$y-\bar{y}$

$(x-\bar{x})^2$

$(y-\bar{y})^2$

$(x-\bar{x})(y-\bar{y})$

10

2

-0.5

-3.5

0.25

12.25

1.75

5

9

-5.5

3.5

30.25

12.25

-19.25

20

10

9.5

4.5

90.25

20.25

42.75

7

1

-3.5

-4.5

12.25

20.25

15.75

$\bar{x}=$ (10+5+20+7)/4

=42/4

=10.5

$\bar{y}=$ (2+9+10+1)/4

=22/4

=5.5

$∑(x-\bar{x})^2=133$

$∑(y-\bar{y})^2=65$

$∑(x-\bar{x})(y-\bar{y})=41$

Coeficiente de Pearson (r) = $\frac{∑(x-\bar{x})(y-\bar{y})}{\sqrt{∑(x-\bar{x})^2}\sqrt{∑(y-\bar{ y})^2}}$

= 41/(√133√65)

Coeficiente de Pearson = 0,44

Pregunta 5: encuentre la fórmula del coeficiente de correlación de Pearson para los datos dados

X	y
1	11
2	22
3	34

Solución:

X y $x-\bar{x}$ $y-\bar{y}$ $(x-\bar{x})^2$ $(y-\bar{y})^2$ $(x-\bar{x})(y-\bar{y})$

1 11 -1 -11.33 1 128.37 11.33

2 22 0 -0.33 0 0.1 0

3 34 1 11.67 1 136.19 11.67

$\bar{x}=2$
$\bar{y}=$ (11+22+34)/3

=67/3

=22,33
$∑(x-\bar{x})^2=2$ $∑(y-\bar{y})^2=264.66$ $∑(x-\bar{x})(y-\bar{y})=23$

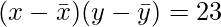
Coeficiente de Pearson (r) = $\frac{∑(x-\bar{x})(y-\bar{y})}{\sqrt{∑(x-\bar{x})^2}\sqrt{∑(y-\bar{ y})^2}}$

= 23/(√2√264,66)

Coeficiente de Pearson = 0,99

Indica que las dos variables x e y dependen directamente una de la otra.

Publicación traducida automáticamente

Artículo escrito por akhilvasabhaktula03 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Coeficiente de correlación de Pearson

Problemas de muestra

Deja una respuesta Cancelar la respuesta