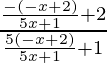Una función es un tipo especial de relación o mapeo entre un conjunto dado de valores de entrada (llamado dominio) y un conjunto de salidas (llamado codominio) donde cada valor del dominio tiene una imagen única en el codominio (llamado rango en este caso). Esto significa que un elemento del dominio puede tener solo una imagen en el codominio, sin embargo, dos elementos del dominio pueden tener la misma imagen.
En el caso de una función, cada elemento del dominio tiene una imagen única en codominio .
La expresión f : A⇢B significa que f es una función

Un ejemplo de un mapeo de funciones.
Otro ejemplo de mapeo de funciones

La primera imagen es una función y la segunda imagen no es una función
La primera imagen muestra un mapeo de funciones, mientras que la segunda imagen no es una función porque un elemento de dominio tiene varias imágenes en codominio.
Tipos de funciones
Función uno-uno (inyectiva): si cada elemento del dominio tiene una imagen distinta en el codominio, se dice que la función es una función uno-uno.

Ejemplo de una función uno a uno.
Función muchos-uno: en este caso, múltiples elementos del dominio pueden tener el mismo mapeo en co-dominio.

Ejemplo de un mapeo de funciones de muchos uno.
Función Onto (Sobreyección): Cuando cada elemento del codominio tiene al menos una preimagen en el dominio, la función se llama función Onto.

Un ejemplo de función onto.
Función Into: en caso de que exista al menos un elemento en el codominio que no tenga una imagen previa en el dominio, se dice que es una función Into.

en función
Funciones biyectivas: una función que es a la vez uno y sobre se conoce como biyección.
¿Puede una función ser igual a su inversa?
Supongamos una función dada y=f(x). la inversa de esta función está representada por f -1 . existe sólo cuando la función dada es biyectiva.
Considere una función f con un dominio de X y un codominio de Y. Supongamos que existe otra función g. Ahora bien, si la composición de estas dos funciones es f(g(x))=x, entonces se dice que las dos funciones f y g son inversas entre sí.
Esto se puede generalizar aún más para verificar si una función dada es la inversa de sí misma. Si la expresión f(f(x))=x (también escrita como fof(x)=x) es cierta para cualquier función f dada, entonces podemos decir que la función es la inversa de sí misma.
Considere que se da una función y= f(x).
Ahora como sabemos si el inverso de f(x) es f -1 (x) entonces
f -1 f(x) =x.
Entonces, para que f(x) sea su propio inverso. f^-1(x)=f(x)
De esto podemos concluir que cuando f^-1(x)=f(x)
Entonces f(f(x)=x.
Esto se puede aplicar en cualquier función para verificar si la función es su propia inversa.
Siempre que una función es su propia inversa, la llamamos función involutiva o involutiva.
Método gráfico
La gráfica de una función es una excelente manera de conocer la naturaleza de la función; al observarla podemos concluir su dominio y su rango y, en algunos casos, podemos conocer los puntos de discontinuidad de esa función. Un gráfico también es útil cuando queremos comparar los valores de dos funciones para el mismo valor de dominio.
Además, otra forma de comprobar si una función es igual a su propia inversa es comparando la gráfica de la función con su inversa. Ahora bien, si la gráfica de la función es igual a su inversa, podemos concluir que la función y su inversa son iguales y la gráfica es una involución.
Cuando se conoce la gráfica de una función, la gráfica de su inversa se puede encontrar tomando su imagen especular a lo largo de la línea y=x. Entonces, si obtenemos la imagen especular de la función igual a la función real, entonces podemos decir que la inversa de esta función es la misma que la función.
Si alguna vez queremos verificar si alguna función es su propia inversa, podemos verificar su imagen especular en la línea y=x. Si la reflexión nos da la misma función entonces es inversa
Ejemplos de preguntas
Pregunta 1: Comprueba si la función lineal f(x)= 9 – x es su propia inversa.
Responder:
Para comprobar si la función es la inversa de sí misma, le aplicamos la operación mencionada anteriormente.
f(x) = 9 – x
fo(x) = 9 -(9 – x) = x
Como se ve arriba fof(x)=x para f(x)=9-x
Por lo tanto f es la inversa de sí misma.
Pregunta 2: Comprueba si la siguiente función es su propia inversa. g(x)=(-x+2) / (5x+1).
Responder:
Dado que,
g(x) = (-x+2) / (5x+1)
gog(x)=
gog(x)=
gog(x)=x.
Por lo tanto, la función g(x) también es su propia inversa .
Pregunta 3: Comprueba si la función h(x)=e x cos x es su propia inversa.
Responder:
Dado que,
h(x) = e x cos x
Por tanto, la función h(x) no es su propia inversa.
Pregunta 4: La función i(x)= ln (e x +1) / (e x +1) se da a comprobar si es una involución.
Responder:
Dado que,
i(x) = ln (ex +1 ) / (ex +1 )
ioi(x)=
.
ioi(x)=
.
ioi(x)= x
Así la función i(x)=
es su propia inversa.
Pregunta 5: j(x)= sen x/(1 + cos x) es una función de x comprueba si es su propio inverso.
Responder:
Dado que,
j(x) = sen x/(1 + cos x)
j(x) = 2 sen (x/2) cos (x/2) / 1+(cos 2 (x/2) – sen 2 (x/2))
j(x) = tan(x/2)
joj(x) = tan(tan(x/2))
Por tanto, la función j(x) no es su propia inversa.
Pregunta 6: considere la función f(x) = 9-x de arriba trace su gráfico y verifique si es una función involutiva
Responder:

Gráfica de la función f(x) e y=x.
Como puede ver, el reflejo de f(x) a lo largo de la línea y=x produce el mismo gráfico que el de f(x). Por tanto, para f(x) la función es igual a su inversa.
Pregunta 2: Comprueba gráficamente si la función g(x) = (-x+2) / (5x + 1) es su propia inversa.
Responder:

gráfica de g(x) y y=x
Dado que la gráfica de la función es simétrica a lo largo de la línea y=x, es su propia inversa.
Publicación traducida automáticamente
Artículo escrito por harmansahani100 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA