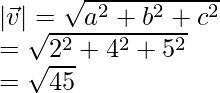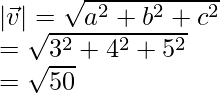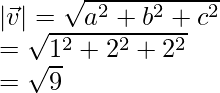Fórmula del vector unitario

Los vectores son entidades geométricas bidimensionales con posición y orientación. Un vector tiene dos puntos: un punto de inicio y un punto final, que refleja la posición final del punto. Sumar, reducir y multiplicar son algunas de las operaciones aritméticas que se pueden realizar con vectores. Un vector unitario se define como un vector con una magnitud de uno.

Vector unitario

El vector unitario de un vector dado es el que se puede obtener dividiendo el primero por su propia magnitud. Un vector unitario es aquel cuya magnitud es igual a uno. Se representa con una letra del alfabeto con una V invertida o gorra encima. Los vectores unitarios tienen una longitud de uno. Los vectores unitarios se usan comúnmente para indicar la dirección de un vector. La dirección de un vector unitario es la misma que la del vector proporcionado, pero su magnitud es una unidad.

Fórmula

$\hat{a}=\frac{\vec v}{|\vec v|}$

dónde,

$\vec v$ denota el vector ai + bj + ck

$|\vec v|$ denota la magnitud del vector v como $\sqrt{a^2 + b^2 + c^2}$

Problemas de muestra

Problema 1. Encuentra el vector unitario de 2i + 4j + 5k.

Solución:

v = 2i + 4j + 5k

$|\vec v| = \sqrt{a^2 + b^2 + c^2} \\= \sqrt{2^2 + 4^2 + 5^2}\\=\sqrt{45}$

= 3√5

Ahora, $\hat{a}=\frac{2i + 4j + 5k}{3√5}$

= (2/3√5) yo + (4/3√5) j + (√5/3)k

Problema 2. Encuentra el vector unitario de 3i + 4j + 5k.

Solución:

v = 3i + 4j + 5k

$|\vec v| = \sqrt{a^2 + b^2 + c^2} \\= \sqrt{3^2 + 4^2 + 5^2}\\=\sqrt{50}$

= 5√2

Ahora, $\hat{a}=\frac{3i + 4j + 5k}{5√2}$

= (3/5√2) yo + (4/5√2) j + (1/√2)k

Problema 3. Encuentra el vector unitario de i + 2j + 2k.

Solución:

v = yo + 2j + 2k

$|\vec v| = \sqrt{a^2 + b^2 + c^2} \\= \sqrt{1^2 + 2^2 + 2^2}\\=\sqrt{9}$

= 3

Ahora, $\hat{a}=\frac{3i + 4j + 5k}{3}$

= (1/3) yo + (2/3) j + (2/3) k

Problema 4. Encuentra el vector unitario del vector resultante de i + 3j +5k y -j – 3k.

Solución:

Vector resultante de i + 3j +5k y -j – 3k = (1+0)i + (3-1)j + (5-3)k

= yo + 2j + 2k

$|\vec v| = \sqrt{a^2 + b^2 + c^2} \\= \sqrt{1^2 + 2^2 + 2^2}\\=\sqrt{9}$

= 3

Ahora, $\hat{a}=\frac{3i + 4j + 5k}{3}$

= (1/3) yo + (2/3) j + (2/3) k

Problema 5. Encuentra el vector unitario de 4i + 4j.

Solución:

v = 4i + 4j + 5k

$|\vec v| = \sqrt{a^2 + b^2 + c^2} \\= \sqrt{4^2 + 4^2}\\=\sqrt{32}$

= 4√2

Ahora, $\hat{a}=\frac{4i + 4j}{4√2}$

= (1/√2) yo + (1/√2) j

Publicación traducida automáticamente

Artículo escrito por parmarraman44 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Vector unitario

Problemas de muestra

Deja una respuesta Cancelar la respuesta