Resolución Completitud y clausulas en Inteligencia Artificial

Requisito previo: 

• Algoritmo de Resolución en Inteligencia Artificial
• IA | Demostración de la resolución en la demostración del teorema proposicional
• IA | Pruebas e inferencias en la demostración del teorema proposicional

Para concluir nuestro tema de resolución, intentaremos comprender por qué PL-RESOLUTION está completo. Para lograrlo, proponemos el cierre de resolución   de una colección de cláusulas  , que es el conjunto de todas las cláusulas derivables de cláusulas en   o sus derivados aplicando la regla de resolución repetidamente. El cierre de la resolución es el valor final de las cláusulas variables calculadas por PL-RESOLUTION . Debido a que solo hay un número limitado de frases separadas que se pueden crear a partir de los símbolos   que existen en S,   debe ser finito. (Tenga en cuenta que sin la fase de factorización, que elimina numerosas copias del literal, esto no sería cierto). Como resultado, PL-RESOLUTION siempre termina.

El teorema de resolución fundamental es un teorema de completitud para la resolución en lógica proposicional: si un grupo de cláusulas no es satisfactoria, la cláusula vacía se incluye en el cierre de resolución de esas cláusulas.

Se demuestra la contrapositiva de este teorema: si la clausura   no contiene la cláusula vacía, entonces   es satisfecha. En realidad, podemos construir un modelo que   incluya valores de verdad apropiados para  . El siguiente es el procedimiento de construcción: Para   de 1 a k, asigne falso a   si una cláusula en   tiene el literal   y todos sus otros literales son falsos bajo la asignación especificada para   De lo contrario,   debe establecerse en verdadero.

Esta asignación a  . Suponga lo contrario: que asignar un símbolo   en algún punto   de la secuencia hace que alguna oración   se vuelva falsa. Para que esto suceda, todos los demás literales ya   deben haber sido falsificados mediante asignaciones a  . Como resultado,   ahora debe parecerse a   o  . Si solo una de estas cláusulas está en  , el algoritmo le dará el valor de verdad necesario a Pi para que sea   verdadera, por lo tanto,   solo se puede falsificar si ambas están en  . Ahora bien, por   estar cerrada en resolución, incluirá la resolutoria de estas dos cláusulas, que tendrán toda su literalidad falsificada por las cesiones a . Esto contradice nuestra creencia de que la primera cláusula falsa entra en escena  . Como resultado, hemos establecido que la construcción nunca falsifica una cláusula en  ; es decir, siempre crea un modelo de  y, por lo tanto, un modelo de S (porque S está incluido en  .

Cláusulas definidas y de cuerno

Es un método de inferencia muy esencial debido a la integridad de la resolución. Sin embargo, en muchos casos, no se requiere toda la fuerza de resolución. Algunas bases de conocimiento del mundo real se adhieren a restricciones particulares sobre los tipos de oraciones que incluyen, lo que les permite emplear un procedimiento de inferencia más limitado y eficiente.

La oración definida, que es una disyunción de literales de los cuales exactamente uno es afirmativo, es una de esas formas restringidas. La oración,   por ejemplo, es una cláusula definida, pero   no lo es.

La cláusula de Horn, que es una disyunción de literales, de los cuales solo uno es afirmativo, es un poco más genérica. Todas las cláusulas definidas, así como las cláusulas sin literales positivos, son cláusulas Horn; se les conoce como cláusulas de objetivo. Las cláusulas Horn se cierran cuando se resuelven: cuando se resuelven dos cláusulas Horn, se devuelve una cláusula Horn.

Esta ecuación muestra una gramática para cláusulas Horn, cláusulas definidas y forma normal conjuntiva. Aunque una cláusula se escribe como   sigue siendo una cláusula definida cuando se escribe como  , solo la primera se considera la forma estándar para las cláusulas definidas. Otro tipo es la   oración, que es una oración CNF con como máximo k literales en cada cláusula.

Solo las bases de conocimiento de cláusulas definidas son interesantes por tres razones:

1. Cada oración definida se puede inferir con un solo literal positivo como conclusión y una conjunción literal positiva como premisa. La frase definida 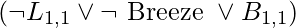 , por ejemplo, puede representarse como la implicación  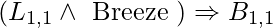 . La frase es más fácil de captar en su forma de implicación: si el agente está en [1,1] y hay viento, entonces [1,1] es brisa. La premisa se conoce como el cuerpo, y la conclusión se conoce como la cabeza en forma de Cuerno. Un hecho es una declaración que consta de un solo literal positivo, como  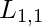.  también se puede expresar en forma de implicación, pero es más fácil escribir simplemente  .
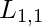2. Las técnicas de enstringmiento hacia adelante y hacia atrás pueden usarse para inferir usando cláusulas de Horn. Ambos algoritmos son naturales en el sentido de que los procesos de inferencia son claros y fáciles de seguir para los humanos. La programación lógica se basa en esta forma de inferencia.
3. Las cláusulas Horn pueden determinar la vinculación en un tiempo proporcional al tamaño de la base de conocimiento, lo cual es una agradable sorpresa.