Requisito previo:
- Pruebas e inferencias en la demostración del teorema proposicional
- Mundo Wumpus en Inteligencia Artificial
Los algoritmos de inferencia basados en el trabajo de resolución utilizan la prueba por contradicción. Para establecer que es ![]() insatisfactorio, demostramos que
insatisfactorio, demostramos que ![]() es insatisfactorio. Hacemos esto demostrando una contradicción.
es insatisfactorio. Hacemos esto demostrando una contradicción.
Las ecuaciones anteriores muestran un algoritmo de resolución. Para empezar, ![]() se transforma a CNF. A continuación, se aplica la regla de resolución a las cláusulas resultantes. Cada par de literales complementarios se resuelve en una nueva cláusula, que se agrega al conjunto si no existía antes. El procedimiento continúa hasta que cualquiera
se transforma a CNF. A continuación, se aplica la regla de resolución a las cláusulas resultantes. Cada par de literales complementarios se resuelve en una nueva cláusula, que se agrega al conjunto si no existía antes. El procedimiento continúa hasta que cualquiera
- no se pueden agregar más cláusulas, en cuyo caso, KB no implica
- dos cláusulas se resuelven para producir la cláusula vacía, en cuyo caso implica KB.
Debido a que una disyunción es verdadera solo si al menos una de sus disyunciones es verdadera, la cláusula vacía, una disyunción sin disyunciones, es idéntica a Falso. Otro enfoque para reconocer que una oración vacía es una contradicción es notar que solo aparece cuando se resuelven dos oraciones unitarias complementarias, como ![]() y .
y .![]()
En el universo wumpus, podemos usar la técnica de resolución para resolver una inferencia muy fácil. No hay brisa cuando el agente está en [1,1], por lo que no se pueden formar pozos en las casillas cercanas. ![]() es la base de conocimiento apropiada, y queremos verificar
es la base de conocimiento apropiada, y queremos verificar ![]() cuál es, digamos,
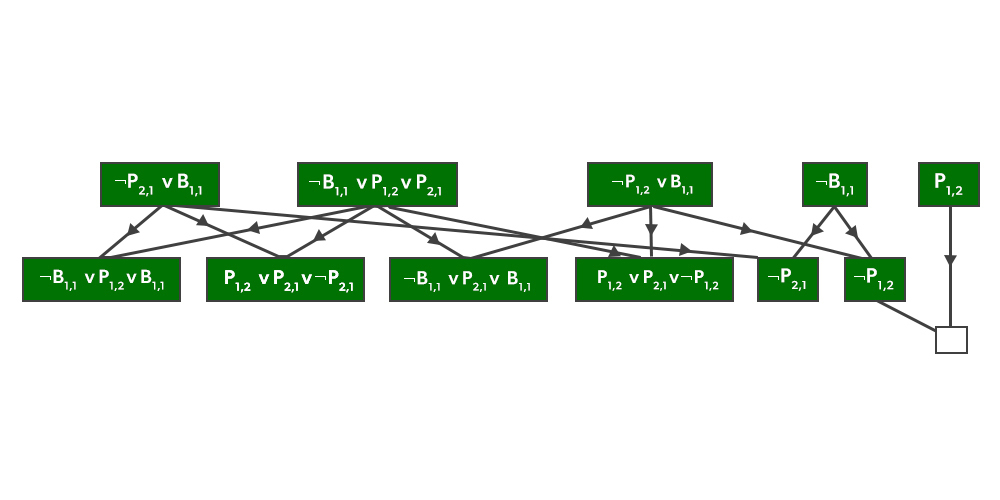
cuál es, digamos, ![]() . Las cláusulas presentadas en la figura anterior se obtienen por conversión
. Las cláusulas presentadas en la figura anterior se obtienen por conversión ![]() a CNF. Las cláusulas derivadas de la resolución de parejas en la primera fila se muestran en la segunda fila de la imagen. La cláusula vacía, representada como un pequeño cuadrado, se obtiene cuando
a CNF. Las cláusulas derivadas de la resolución de parejas en la primera fila se muestran en la segunda fila de la imagen. La cláusula vacía, representada como un pequeño cuadrado, se obtiene cuando ![]() se resuelve con
se resuelve con ![]() . La figura anterior ilustra que muchas de las etapas de resolución son innecesarias. Por ejemplo, la frase
. La figura anterior ilustra que muchas de las etapas de resolución son innecesarias. Por ejemplo, la frase ![]() es idéntica a
es idéntica a ![]() lo que equivale a
lo que equivale a ![]() . No es particularmente útil deducir que eso
. No es particularmente útil deducir que eso ![]() es cierto. Como resultado, se puede eliminar cualquier frase que contenga dos literales complementarios.
es cierto. Como resultado, se puede eliminar cualquier frase que contenga dos literales complementarios.
Publicación traducida automáticamente
Artículo escrito por Mohit Gupta_OMG 🙂 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
