La curvatura es ese valor escalar por el cual una curva se desvía de ser plana a una curva y de una curva a una línea. El recíproco de la curvatura es el radio de curvatura y es un círculo imaginario en lugar de una forma o figura genuina. El radio de curvatura es el radio del círculo aproximado en un lugar específico. Se representa por la longitud del vector de curvatura y se denota con el símbolo R. Se define como la distancia entre el vértice y el centro de curvatura. A medida que avanza la curva, el radio cambia.

Fórmula del radio de curvatura
El radio de curvatura de una curva se define como el radio aproximado de un círculo en cualquier punto dado o la longitud del vector de una curvatura. Existe para cualquier curva con la ecuación y = f(x) con x como su parámetro.
Radio de curvatura, R =
dónde,
dy/dx = primera derivada de la función y = f(x),
d 2 y/dx 2 = segunda derivada de la función y = f(x).
En el caso de coordenadas polares r=r(θ), el radio de curvatura viene dado por
dónde,
K es la función vectorial tangente y la curvatura de la curva dada por dT/ds,
r es el radio de curvatura.
Problemas de muestra
Problema 1. Encuentra el radio de curvatura para f(x) = 4x 2 + 3x – 7 en x = 4.
Solución:
Tenemos, y = 4x 2 + 3x – 7 y x = 4.
dy/dx = 16x + 3
d 2 y/dx 2 = 16
Usando la fórmula del radio de curvatura, obtenemos
R = (1 + (16x + 3) 2 ) 3/2 /16
= (1 + 256x 2 + 9 + 36x) 3/2 /16
= (256x 2 + 36x + 10) 3/2 /16
Sustituye el valor x = 4.
R = (256 (4) 2 + 36 (4) + 10) 3/2 /16
= (4096 + 144 + 10) 3/2 /16
= 27066/16
= 1691.625 unidades
Problema 2. Encuentra el radio de curvatura para f(x) = 3x 2 + 3x – 2 en x = 1.
Solución:
Tenemos, y = 3x 2 + 3x – 2 y x = 1.
dy/dx = 6x + 3
d 2 y/dx 2 = 6
Usando la fórmula del radio de curvatura, obtenemos
R = (1 + (6x + 3) 2 ) 3/2 /6
= (1 + 36x 2 + 9 + 36x) 3/2 /6
= (36x 2 + 36x + 10) 3/2 /6
Sustituye el valor x = 1.
R = (36 (1) 2 + 36 ( 1 ) + 10) 3/2/6
= (36 + 36 + 10) 3/2 /6
= 742,54/6
= 123,75 unidades
Problema 3. Encuentra el radio de curvatura para f(x) = 3x 3 – 2x + 7 en x = 2.
Solución:
Tenemos, y = 3x 3 – 2x – 2 y x = 2.
dy/dx = 9x 2 – 2
d 2 y/dx 2 = 18x
Usando la fórmula del radio de curvatura, obtenemos
R = (1 + (9x 2 – 2) 2 ) 3/2 /18x
= (1 + 81x 4 + 4 – 36x 2 ) 3/2 /18x
= (81x 4 – 36x 2 + 5) 3/2 /18x
Sustituye el valor x = 2.
R = (81 (2) 4 – 36 (2) + 5) 3/2/18 (2)
= (576 – 72 + 5) 3/2 /36
= 12305.26/36
= 512,71 unidades
Problema 4. Encuentra el radio de curvatura para f(x) = 5x 3 – 3x 2 + x en x = 1.
Solución:
Tenemos, y = 5x 3 – 3x 2 + x y x = 1.
dy/dx = 15x 2 – 6x + 1
d 2 y/dx 2 = 30x – 6
Usando la fórmula del radio de curvatura, obtenemos
R = (1 + (15x 2 – 6) 2 ) 3/2 /(30x – 6)
= (1 + 225x 4 + 36 – 180x 2 ) 3/2 /(30x – 6)
= (225x 4 – 180x 2 + 37) 3/2 /(30x – 6)
Sustituye el valor x = 1.
R = (225(1) 4 – 180(1) 2 + 37) 3/2 /(30 (1) – 6)
= (225 – 180 + 37) 3/2 /24
= 742,54/24
= 30,93 unidades
Problema 5. Hallar el radio de curvatura de la curva f(x) = x 2 .
Solución:
Tenemos la curva, y = x 2
dy/dx = 2x
d 2 y/dx 2 = 2
Usando la fórmula del radio de curvatura, obtenemos
R = (1 + (2x) 2 ) 3/2 /2
= (1 + 4x 2 ) 3/2 /2
= (1 + 4 años) 3/2 /2
Problema 6. Hallar el radio de curvatura de la curva f(x) = sen x.
Solución:
Tenemos la curva, y = sen x.
dy/dx = cos x
d 2 y/dx 2 = – sen x
Usando la fórmula del radio de curvatura, obtenemos
R = – (1 + (cos x) 2 ) 3/2 /sen x
= (1 + cos 2 x) 3/2 /sen x
= (1 + cos 2 x) 3/2 /y
Problema 7. Hallar el radio de curvatura de la curva f(x) = e x .
Solución:
Tenemos la curva, y = e x .
dy/dx = e x
re 2 y/dx 2 = e x
Usando la fórmula del radio de curvatura, obtenemos
R = – (1 + (e x ) 2 ) 3/2 /e x
= (1 + e 2x ) 3/2 /e x
= (1 + y 2 ) 3/2 / año
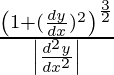
![Rendered by QuickLaTeX.com \rho=\frac{1}{K}\frac{\left[r^2+(\frac{dr}{d\theta})^2\right]^{\frac{3}{2}}}{\left|r^2+2(\frac{dr}{d\theta})^2-r\frac{d^2r}{d\theta^2}\right|}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1e336a2b2d7fd013c249591534f80f18_l3.png)