¿Qué es el relleno en la red neuronal?

Como sabemos, mientras construimos una red neuronal, estamos haciendo convolución para extraer características con la ayuda de kernels con respecto a los conjuntos de datos actuales, que es la parte importante para que su red aprenda mientras convoluciona.

Por ejemplo, si desea entrenar su red neuronal para clasificar si es un perro o un gato, al aplicar la convolución, los núcleos extraerán características de las imágenes como la oreja de un perro y la cola de un perro mucho más para diferenciarse. entre las características de perro y gato, así es como funciona la convolución.

Como puede ver en la imagen de arriba, si convoluciona 3 X 3 núcleos en un tamaño de imagen de entrada de 6 x 6, el tamaño de la imagen se reducirá en 2, ya que el tamaño del núcleo es 3 con una salida de 4 x 4 aplicando 3 x 3 en El tamaño de 4 x 4 se reducirá a 2 x 2 como se ve en la imagen de arriba. Pero si va a aplicar 3 x3 ahora, no podemos convolucionar más ya que el tamaño de la imagen de salida es 2 x 2 ahora, ya que matemáticamente obtendrá una dimensión negativa que no es posible.

Pero si observa que puede suceder, nuestra red no considerará algunas de las características importantes porque terminamos con solo 2 convoluciones que, por lo tanto, son difíciles de encontrar. Todas las características se extraen para diferenciar entre dos objetos con los que está entrenando la red neuronal.

¿Por qué el tamaño de la imagen se reduce solo en 2?

Tenemos la fórmula para calcular el tamaño de la imagen de salida que es:

Donde O representa el tamaño de la imagen de salida, n es el tamaño de la imagen de entrada y k es el tamaño del kernel.

Si observa el ejemplo anterior, tenemos un tamaño de imagen de entrada de 6 x 6 con un tamaño de kernel de 3 x 3. Por lo tanto, el tamaño de salida después de aplicar la primera convolución será

O = 6 - 3 + 1
O = 4 x 4

Esta es una de las razones por las que Padding entra en escena

¿Por qué necesitamos relleno?

• El objetivo principal de la red es encontrar la característica importante en la imagen con la ayuda de capas convolucionales, pero puede suceder que algunas características sean la esquina de la imagen que el núcleo (extractor de características) visite muy pocas veces debido a que podría haber una posibilidad de perder parte de la información importante.
• Por lo tanto, el relleno es la solución en la que agregamos píxeles adicionales alrededor de las 4 esquinas de la imagen, lo que aumenta el tamaño de la imagen en 2, pero debe ser lo más neutral posible, lo que significa que no altera las características de la imagen original de ninguna manera para que sea complicado para el red para aprender más. Además, podemos agregar más capas ya que ahora tenemos una imagen más grande.

Podemos decir para facilitar la comprensión que el relleno ayuda al núcleo (extractor de características) a visitar los píxeles de la imagen alrededor de las esquinas más veces para extraer características importantes para un mejor aprendizaje.

Si ve la imagen a continuación que muestra una ilustración de cómo el kernel visita los píxeles de la imagen, es importante que el kernel visite cada píxel al menos más de 1 vez o 2 veces para extraer las características importantes.

Eche un vistazo a la imagen de arriba mientras gira alrededor de la imagen con el kernel como píxeles alrededor de las esquinas de la imagen visitada por el kernel en muy poco tiempo en comparación con la parte media de los píxeles.

Si puede observar en la imagen de arriba, hemos agregado el relleno de cero alrededor de las 4 esquinas de la imagen y el tamaño de la imagen de entrada aumentó de 6 x 6 a 8 x 8 después de aplicar la primera convolución. El tamaño de la imagen de salida sería 6 x 6, es decir. lo que queremos según la pregunta anterior.

Después de aplicar el relleno, podemos observar que existe la posibilidad de convolucionar una vez más en comparación con sin relleno, lo que ayuda a la red a extraer más funciones para un mejor aprendizaje al mismo tiempo. Incluso aplicar el relleno nos ayuda a convolucionar una vez más, lo que ayuda a la red a extraer más funciones para un mejor aprendizaje al mismo tiempo.

Si ve la imagen a continuación y así es como se ve la imagen rellenada:

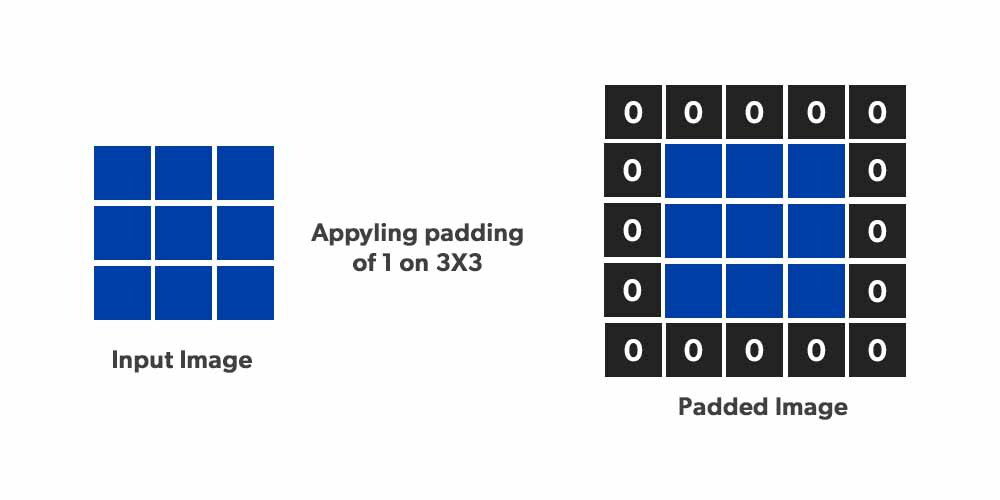
Hay dos tipos de relleno

• Relleno válido donde no aplicamos ningún relleno & P=0
• Mismo relleno donde el tamaño de las imágenes de salida debe ser igual al tamaño de la imagen de entrada debido a que hemos aplicado el mismo relleno.

De la fórmula anterior tenemos:

Ahora, estamos agregando relleno sobre los 4 lados de una imagen hacia abajo, arriba, derecha e izquierda agregando relleno cero. (NOTA: Aquí no estamos considerando avances)

Veamos una nueva fórmula con relleno.

Si ve el mismo relleno O = n (el tamaño de la imagen de salida debe ser igual al tamaño de la imagen de entrada)

Entonces,   desde aquí podemos usar simplemente matemáticas en la ecuación anterior mencionada 

¿Por qué siempre usamos núcleos impares como 3 x 3, 5 x 5, etc., por qué no núcleos 4 x 4 (incluso núcleos)?

Por ejemplo, si desea utilizar un núcleo de 4 x 4 , ¿cuál será el relleno que deberá utilizar?

Puedes usar la fórmula anterior p =( k – 1)/2

Tenemos núcleo = 4 x 4

p = 4 -1/2 = 3/2 = 1,5

Lo que significa que debe agregar 1,5 píxeles alrededor de las 4 esquinas de la imagen para aplicar relleno , lo que a su vez no es posible porque no podemos agregar 1,5 píxeles , sino que solo podemos agregar los píxeles en números enteros como 1,2,3,4 ,5,6 y 7, etc. píxeles alrededor de las esquinas de la imagen.

Esta es una de las razones por las que los núcleos son siempre un número impar, de modo que podemos agregar un número entero de píxeles alrededor de la imagen para extraer más funciones, ya que agregar 1,5 píxeles alrededor no tiene ningún sentido y es difícil agregar al mismo tiempo. .

¿Por qué siempre usamos padding = 1 ? ¿Qué queremos decir cuando decimos que está usando padding de 1 ? En todas las redes estándar notará que el padding usado siempre es 1, ya que simplemente mientras estamos rellenando estamos agregando información al nosotros mismos y no es una buena idea interferir con la red que mucho como las mejores características aprendidas por la red es el autoaprendizaje una vez y también aumentará mucho el tamaño de entrada y hará que el modelo sea pesado.

¿Por qué «relleno cero»?

Ahora, una de las preguntas que surgen en nuestra mente es por qué la gente siempre usa el relleno cero (0) ciegamente simplemente siguiendo lo que hemos leído en los blogs o en cualquier curso. Entonces, ahora entendemos cómo funciona el relleno y cómo es importante para una red neuronal. Pero siempre nos viene una pregunta a la cabeza, ¿por qué solo 0 relleno? ¿Por qué no podemos usar 1-padding o cualquier número?

Cuando normalizamos una imagen, el rango de píxeles va de 0 a 1, y si no se ha normalizado , el rango de píxeles será de 0 a 255.

Si consideramos ambos casos, podemos ver que 0 es el número mínimo. Entonces, usar 0 se convierte en una forma más genérica de hacer esto. Además, tiene sentido computacionalmente ya que estamos considerando el número mínimo entre esos píxeles.

Pero no siempre es 0. Considere un caso en el que tenemos valores que van desde -0.3 a 0.3 , en este caso, el número mínimo es -0.3, y si usamos el relleno de 0 alrededor, sería gris en lugar de negro . . El mismo caso se da cuando tenemos una función de activación como tanh, que oscila los valores de -1 a 1, en este caso, el valor mínimo es -1., por lo que estaríamos usando (-1) padding en lugar de 0 paddings, para agregar píxeles negros a su alrededor. Si usamos 0 rellenos, entonces sería un límite de color gris en lugar de un color negro.

Pero aquí hay un problema , no siempre es posible calcular qué sucederá con los valores de inactivación, por lo que buscamos un valor neutral que pueda satisfacer la mayoría de los casos sin problemas, y aquí es donde el relleno 0 nos salva. Si consideramos los dos rangos mencionados anteriormente, podemos ver que el uso del relleno 0 daría un límite gris en lugar de negro, lo cual no es una gran pérdida. También podemos llamar a estos casos, «El Caso de Relleno Mínimo», donde estamos considerando el valor mínimo entre los mapas de activación.

La mayoría de las veces, usamos relu entre capas, por lo que en el caso de relu, 0 se convierte en el valor mínimo y es por eso que es tan popular y genérico.

¿Necesitamos agregar relleno en cada capa?

Entendamos esto con la ayuda de un ejemplo, permite que el conjunto de datos del reconocedor de dígitos MNIST

Aquí hay algunas imágenes de muestra del conjunto de datos MNIST. Arriba discutimos dos razones principales para usar el relleno:

• Reducción de la salida después de la convolución, por lo que podemos agregar más capas para extraer más características
• Agregar para salvar la pérdida de información alrededor de los bordes

Puede ver que los números en el conjunto de datos no están alrededor de los bordes, están principalmente en el centro. Eso significa que puede haber muy poca información alrededor de los bordes. Entonces, la razón principal para agregar relleno, en este caso, es agregar más capas. Pero también MNIST no requiere tantas capas. Puede agregar relleno en las capas iniciales, pero en todas las capas sería de mucha utilidad, solo hará que su modelo sea más pesado.

En conclusión, depende de los conjuntos de datos y de la declaración del problema, qué capas requerirán relleno.