Lasso vs Ridge vs red elástica | ML

Sesgo:
los sesgos son las suposiciones subyacentes que hacen los datos para simplificar la función objetivo. El sesgo nos ayuda a generalizar mejor los datos y hace que el modelo sea menos sensible a puntos de datos únicos. También disminuye el tiempo de entrenamiento debido a la disminución de la complejidad de la función objetivo. Un alto sesgo sugiere que se asume más la función objetivo. Esto conduce a veces a la desadaptación del modelo.
Los ejemplos de algoritmos de alto sesgo incluyen regresión lineal, regresión logística, etc.

Varianza:
en el aprendizaje automático, la varianza es un tipo de error que ocurre debido a la sensibilidad de un modelo a las pequeñas fluctuaciones en el conjunto de datos. La alta varianza haría que un algoritmo modelara los valores atípicos/ruido en el conjunto de entrenamiento. Esto se conoce más comúnmente como sobreajuste. En esta situación, el modelo básicamente aprende cada punto de datos y no ofrece una buena predicción cuando se prueba en un nuevo conjunto de datos.
Los ejemplos de algoritmos de alta varianza incluyen el árbol de decisión, KNN, etc.

Sobreadaptación vs. Falta de ajuste vs Justo a la derecha

Error en regresión lineal:
Consideremos un modelo de regresión simple que tiene como objetivo predecir una variable Y, a partir de la combinación lineal de las variables X y un término de error normalmente distribuido. $\epsilon$

$Y = \beta * X + \epsilon$

dónde
$\epsilon$
es la distribución normal que añade algo de ruido en la predicción.

Aquí $\beta$ está el vector que representa el coeficiente de las variables en la X que necesitamos estimar a partir de los datos de entrenamiento. Necesitamos estimarlos de tal manera que produzca el error residual más bajo. Este error se define como:

$L_{ols}({\hat{\beta}})= \sum_{i=0}^{n} \left \| y_{i} - x_{i} * \hat{\beta_{i}} \right \|^2 = \left \| Y - X * \hat{\beta} \right \|^{2}$

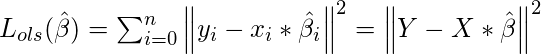
Calcular
$\hat{\beta}$
usamos la siguiente transformación matricial.
$\hat{\beta_{ols}} = \left ( X^{T}X \right )^{-1}\left ( X^{T}Y \right )$
Aquí sesgo y varianza de
$\hat{\beta}$
Puede ser definido como:
$Bias(hat{\beta}) = E\left ( \hat{\beta} \right ) - \beta$
y
$Variance\left ( \hat{\beta} \right ) =\sigma ^{2}\left ( {X}'X \right )^{-1}$
Podemos simplificar el término de error de la ecuación OLS definida anteriormente en términos de sesgo y varianza de la siguiente manera:

$Error-term = \left ( E\left ( X\hat{\beta} \right ) - X\beta \right )^{2} +E\left ( X\hat{\beta} - E\left ( X\hat{\beta} \right ) \right )^{2}+\sigma^{2}$

El primer término de la ecuación anterior representa
Sesgo ²
. El segundo término representa
Diferencia
y el tercer término (
$\sigma^{2}$
) es un término de error irreducible.

Varianza/sesgo vs error

Compensación de sesgo vs varianza

Visualización de varianza-sesgo

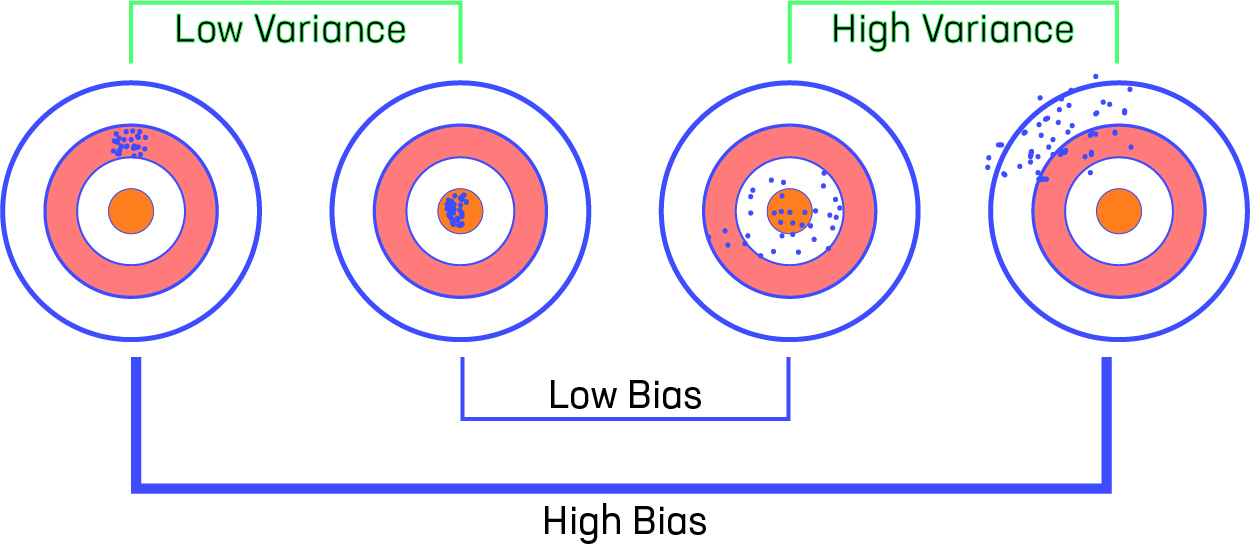
Consideremos que tenemos un modelo muy preciso, este modelo tiene un error bajo en las predicciones y no es del objetivo (que está representado por la diana). Este modelo tiene un sesgo y una varianza bajos. Ahora, si las predicciones están dispersas aquí y allá, ese es el símbolo de una alta varianza, también si las predicciones están lejos del objetivo, entonces ese es el símbolo de un alto sesgo.
A veces tenemos que elegir entre baja varianza y bajo sesgo. Hay un enfoque que prefiere cierto sesgo a una alta varianza, este enfoque se llama Regularización . Funciona bien para la mayoría de los problemas de clasificación/regresión.

Regresión de Ridge:
en la regresión de Ridge, agregamos un término de penalización que es igual al cuadrado del coeficiente. El término L2 es igual al cuadrado de la magnitud de los coeficientes. También agregamos un coeficiente $\lambda$ para controlar ese término de penalización. En este caso, si $\lambda$ es cero, entonces la ecuación es el MCO básico; de lo contrario $\lambda \, > \, 0$ , agregará una restricción al coeficiente. A medida que aumentamos el valor de $\lambda$ esta restricción, el valor del coeficiente tiende a cero. Esto conduce a la compensación de un mayor sesgo (las dependencias de ciertos coeficientes tienden a ser 0 y de ciertos coeficientes tienden a ser muy grandes, lo que hace que el modelo sea menos flexible) por una varianza más baja.

$L_{ridge} = argmin_{\hat{\beta}}\left ({\left \| Y- \beta * X \right \|}^{2} + \lambda * {\left \| \beta \right \|}_{2}^{2} \right )$

dónde
$\lambda$
es sanción de regularización.

Limitación de la regresión de cresta: la regresión de cresta disminuye la complejidad de un modelo, pero no reduce el número de variables, ya que nunca lleva a que un coeficiente sea cero, sino que solo lo minimiza. Por lo tanto, este modelo no es bueno para la reducción de características.

Regresión de lazo:
la regresión de lazo significa Operador de selección y contracción mínima absoluta. Agrega un término de penalización a la función de costo. Este término es la suma absoluta de los coeficientes. A medida que el valor de los coeficientes aumenta desde 0 , este término penaliza, modelo de causa, disminuir el valor de los coeficientes para reducir la pérdida. La diferencia entre la regresión ridge y lazo es que tiende a hacer que los coeficientes lleguen al cero absoluto en comparación con Ridge, que nunca establece el valor del coeficiente en el cero absoluto.

$L_{lasso} = argmin_{\hat{\beta}}\left ({\left \| Y- \beta * X \right \|}^{2} + \lambda * {\left \| \beta \right \|}_{1} \right )$

Limitación de la regresión de Lasso:

Lasso a veces tiene problemas con algunos tipos de datos. Si el número de predictores (p) es mayor que el número de observaciones (n) , Lasso elegirá como máximo n predictores distintos de cero, incluso si todos los predictores son relevantes (o pueden usarse en el conjunto de prueba).
Si hay dos o más variables altamente colineales, la regresión LASSO selecciona una de ellas al azar, lo que no es bueno para la interpretación de los datos.

Red elástica:
a veces, la regresión de lazo puede causar un pequeño sesgo en el modelo donde la predicción depende demasiado de una variable en particular. En estos casos, se demuestra que la red elástica combina mejor la regularización tanto de lazo como de cumbrera. La ventaja de que no elimina fácilmente el alto coeficiente de colinealidad.

$L_{elasticNet} = argmin_{\hat{\beta}}\left ( \hat\beta \right )\left ( \sum \left ( y - x_i^J\hat{\beta} \right )^2 \right )/2n + \lambda \left ( (1 -\alpha )/2 * \sum_{j=1}^{m} \hat{\beta_{j}^{2}} + \alpha * \sum_{j=1}^{m} \left \| \hat{\beta_{j}} \right \| \right)$

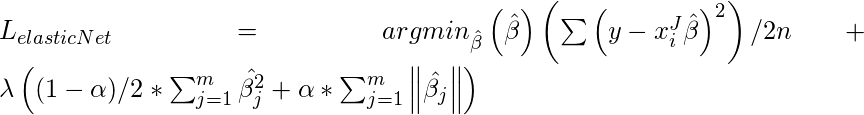
Referencia – Papel de red elástica

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta