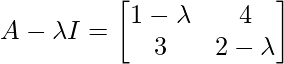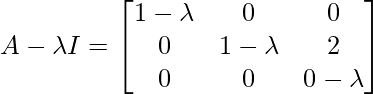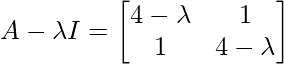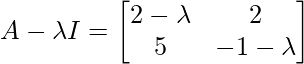El valor propio se define como un escalar asociado con una transformación lineal dada de un espacio vectorial y que tiene la propiedad de que existe un vector distinto de cero que, cuando se multiplica por el escalar, es igual al vector obtenido al permitir que la transformación opere en el vector. Las raíces del sistema matricial de ecuaciones lineales también se denominan valores propios. Considere una array cuadrada A de kxk, v es un vector y λ es la cantidad escalar que se puede representar como,
Av = λv
Av – λv = 0 ⇢ [λ – Valor propio]
A – λI = 0 ⇢ [I – Array identidad]
|A – λI| = 0
Propiedades del valor propio
Considere una array cuadrada A con valores propios λ 1 , λ 2 … λ n
- La determinación de A es un producto de todos sus valores propios. [det(A) = λ 1 × λ 2 ….λ norte ]
- La array A es invertible si y solo si todos los valores propios son distintos de cero.
- Los valores propios de las arrays simétricas y hermitianas reales son iguales.
- Los valores propios de las arrays hermitianas sesgadas y simétricas reales son puros o cero.
- Los valores propios de arrays unitarias y ortogonales son de módulo unitario |λ| = 1.
- Valor propio de A -1 = 1/λ 1 ,1/λ 2 ,… 1/λ n.
- Valor propio de A k = λ k 1 , λ k 2 , …. λ k norte
- Si A y B son dos arrays del mismo orden entonces, Valor propio de AB = Valor propio de BA.
- Si una array cuadrada A es una array triangular inferior/superior, entonces su valor propio serán los elementos diagonales de la array.
Pasos para hallar el valor de una array
A continuación se muestran los pasos que se deben seguir para encontrar el valor de una array,
Paso 1: Compruebe si la array dada es una array cuadrada o no. En caso afirmativo, siga el paso 2.
Paso 2: Determinar la array identidad (I)
Paso 3: Estimar la array A – λI.
Paso 4: Encuentra el determinante de A – λI.
Paso 5: Igualar el determinante de A-λI a cero. {|A – λI| = 0}
Paso 6: Calcula todos los valores posibles de λ.
Problemas de muestra
Pregunta 1: Encuentre el valor propio de la array 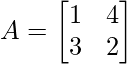 .
.
Solución:
|A – λI|= 0
(1 – λ)(2 – λ) – 12 = 0
2 – λ – 2λ + λ 2 – 12 = 0
λ 2 – 3λ – 10 = 0
λ 2 – 5λ + 2λ – 10 = 0
(λ + 2)(λ – 5) = 0
λ = -2, 5
Por lo tanto, el valor propio será (-2, 5)
Pregunta 2: Encuentra el valor propio de la array 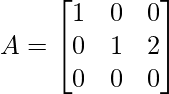
Solución:
|A – λI| = 0
(1 – λ)[(1 – λ)(0 – λ) – 2] = 0
(1 – λ)(λ 2 – λ – 2) = 0
-λ 3 + 2λ + λ – 2 = 0
l = 1, 0
Por lo tanto, el valor propio será 1, 0.
Pregunta 3: Encuentra el valor propio de la array 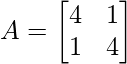
Solución:
[(4 – λ)(4 – λ)] – 1 = 0
16 – 4λ – 4λ + λ 2 – 1 = 0
λ 2 – 8λ + 15 = 0
λ 2 – 3λ – 5λ + 15 = 0
λ(λ – 3) – 5(λ – 3) = 0
(λ – 5)(λ – 3) = 0
λ = 5, 3
Por lo tanto, el valor propio será 5, 3
Pregunta 4: Encuentre el valor propio de la array dada 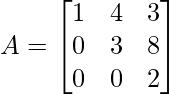
Solución:
Como se mencionó anteriormente en las propiedades del valor propio, es decir, si una array cuadrada A es una array triangular inferior/superior, entonces su valor propio serán los elementos diagonales de la array.
Como la array A dada es una array triangular inferior, su valor propio será 1, 3, 2.
Pregunta 5: Encuentra el valor propio de la array 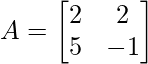
Solución:
[(2 – λ)(-1 – λ)] – 10 = 0
-2 – 2λ + λ + λ 2 – 10 = 0
λ 2 – λ – 12 = 0
λ 2 – 4λ + 3λ – 12 = 0
λ(λ – 4) + 3(λ – 4) = 0
(λ – 4)(λ + 3) = 0
λ = 4, -3
Por lo tanto, el valor propio será 4, -3
Pregunta 6: Encuentra el valor propio de la array 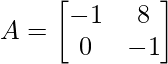
Solución:
|A – λI| = 0
(-1 – λ) 2 – 0 = 0
(λ + 1) 2 = 0
λ = -1
Por lo tanto, el valor propio será -1
Publicación traducida automáticamente
Artículo escrito por 69406930ravi y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA