¿Cómo encontrar Derivados?

En la vida diaria, las personas a menudo se enfrentan a cuestiones como «¿Cómo responde el paciente a las dosis proporcionadas?» o “¿cómo se altera la ganancia en relación con el costo de producción del producto?” o «¿Cuál es la tasa de cambio en la presión de un gas en relación con su volumen?» o «¿Cuál es la tasa de cambio de la velocidad en relación con el tiempo?» y muchos más. Si uno observa cuidadosamente, puede ver que estas preguntas están relacionadas con la tasa de cambio de una cantidad variable con respecto al cambio correspondiente en otra. Tal medida de tasa se llama derivada.

La derivada también se puede utilizar para calcular la ecuación de la tangente y la normal a la curva en un lugar determinado, así como los valores máximo y mínimo de una función y sus valores estimados. Ejemplo,

Un biólogo usa derivados para calcular la tasa de crecimiento bacteriano en cultivo.
Es utilizado por un ingeniero eléctrico para describir el cambio en la corriente en un circuito eléctrico.

Derivada en un punto

Supongamos que una función f(x) está definida en una vecindad de a.

Si a y a + h pertenecen al conjunto del dominio de una función f y

$\lim\;_{h \to 0}\;\frac{f(a + h) - f(a)}{h}$

existe, entonces este límite se llama la derivada de f(x) en x = a y se denota por,

f’ (a) o [df / dx]x = a

De este modo,

$f'(a) = \lim\;_{h \to a}\; \frac{f(a + h) - f(a)}{h}$

En general, la derivada de una función en cualquier punto x viene dada por,

$f'(x) = \lim\;_{h \to 0} \; \frac{f(x + h) - f(x)}{h} = \frac{df}{dx}$

Esto se conoce como primer principio de la derivada.

Nota: Si existe la derivada de f(x), entonces se dice que la función f es derivable o derivable. La diferenciación es el proceso de encontrar derivadas.

Interpretación Geométrica de la Derivada

Considere el siguiente gráfico,

Considere la función f(x) definida en un intervalo abierto (a, b). Sea P un punto en la curva y = f(x). Sean Q[(c – h), f(c – h)] y R el punto a cada lado del punto P. Ahora,

La pendiente de la cuerda PQ es, f(c – h) – f(c) / (-h).

La pendiente de la cuerda PR se puede escribir como, f(c + h) – f(c) / h

Ahora, sabemos que la tangente a una curva en un punto P es la posición límite de la secante PQ cuando Q tiende a P.

De manera similar, también es la posición límite de la secante PR cuando R tiende a P.

∴ como h⇢ 0 puntos Q y R ambos tienden a P desde los lados izquierdo y derecho.

∴ La pendiente de la tangente en el punto P es,

$P = \lim \;_{Q \to P} \;(Slope\ of\ secant\ PQ)$

$\lim \;_{h \to 0} \;(Slope\ of\ secant\ PQ)$

$\lim \;_{Q \to P} \; \frac{f(c + h) - f(c)}{h}$

Si estos límites existen y son iguales, existe una única tangente en el punto P.

La pendiente de la tangente se denota por dy / dx, es decir, f'(x)

De este modo,

$f'(x) = \lim\;_{h \to 0} \; \frac{f(c + h) - f(c)}{h}$

$= \lim\;_{h \to 0} \; \frac{f(c - h) - f(c)}{-h}$

Derivada de una función estándar

Función constante

Sea f(x) = k donde k es cualquier constante

∴ f(x + h) = k

Considerar,

$\lim\;_{h \to 0}\; \frac{f(x + h) - f(x)}{h}$

$=\lim\;_{h \to 0}\; \frac{k - k}{h}$

= 0

∴ re(k) / dx = 0

Función de potencia

Sea f(x) = xn

f(x + h) = (x + h)n , n∈ R

Considerar,

$\lim\;_{h \to 0}\; \frac{f(x + h) - f(x)}{h}$

$=\lim\;_{h \to 0}\; \frac{(x + h)^n - x^n}{h}$

$= \lim\;_{h \to 0}\; \frac{[x^n \;+ \; nx^{n - 1}h \; + \; \frac{n(n-1)}{2!} x^{x-2}h^2 \; + .... + h^n] - x^n}{h}$

$= \lim\;_{h \to 0}\;\frac{h}{h}[nx^{n-1}\;+\;\frac{(n-1)}{2!}x^{n-2}h\;+......+\;h^{n-1}]$

$= \lim\;_{h \to 0}\; [nx^{n-1}\;+\;\frac{n(n-1)}{2!}x^{n-2}h\;+.....+h^{n-1}]$

=[ nxn-1 + 0 + …….+ 0]

= nxn-1

∴ d(xn) / dx = n xn-1

Nota: d(xk) / dx = kxk-1, para cualquier número real k

Funciones trigonométricas

Sea f(x) = sen x

f(x + h) = sen(x + h)

Aquí,

$\lim\;_{h \to 0}\; \frac{f(x + h) - f(x)}{h}$

$= \lim\;_{h \to 0}\; \frac {sin(x + h) - sin \;x}{h}$

$=\lim\;_{h \to 0}\; \frac{2cos(\frac{x + h + x}{2})sin\frac{x + h -x}{2}}{h}$

$=\frac{2}{2}\lim\;_{h \to 0} \;cos(\frac{2x + h}{2}) \lim\;_{h \to 0}\; \frac{sin \;h/2}{h/2})$

= coseno (x + 0).1

= cos x

∴ d(sen x) / dx = cos x

Similarmente,

d(cos x) / dx = – sen x

d(tan x) / dx = seg2 x

d(cot x) / dx = – cosec2 x

d(seg x) / dx = seg x . bronceado x

d(coseg x) / dx = – cosec x . cuna x

Función exponencial y logarítmica

d(hacha) / dx = hacha . log a {a > 0 y a ≠ 1}

d(ex) / dx = ex

d(log x) / dx = 1 / x

Reglas de diferenciación

Derivada de la suma (Teorema 1)

Enunciado: Si u y v son funciones derivables de x y si y = u + v entonces dy / dx = du / dx + dv / dx.

Prueba:

Sean δu, δv y δy los pequeños incrementos en u, v, y respectivamente, correspondientes al incremento δx en x

Como δx ⇢ 0, δu⇢ 0, δv⇢ 0, δy ⇢ 0,

Como u y v son funciones diferenciables de x,

$\frac{du}{dx} = \lim\;_{\delta x \to0}\;\frac{\delta u}{\delta x} \; and \; \frac{dv}{dx}\lim\;_{\delta x \to0}\;\frac{\delta v}{\delta x}$

y = u + v ⇢ ecuación (1)

y + δy = (u + δu) + (v + δv) ⇢ ecuación (2)

Restando (1) de (2) obtenemos,

δy = δu + δv

Dividiendo ambos lados por δx,

δy / δx = δu / δx + δv / δx

Tomando el límite como δx ⇢ 0, en ambos lados,

$\lim\;_{\delta x \to 0}\;\frac{\delta y}{\delta x} = \;\lim\;_{\delta x \to 0}\;[\frac{\delta u}{\delta x} \;+\;\frac{\delta v}{\delta x} ]$

$\lim\;_{\delta x \to 0}\;\frac{\delta y}{\delta x} = \;\lim\;_{\delta x \to 0}\;\frac{\delta u}{\delta x} \;+\lim\;_{\delta x \to 0}\;\frac{\delta v}{\delta x}$

du / dx + dv / dx

$\therefore \lim\;_{\delta x\to0}\; \frac{\delta y}{\delta x }$

∴ dy/dx = du/dx + dv/dx

Similarmente,

Derivada de la diferencia (Teorema 2)

Enunciado : Si u y v son funciones diferenciables de x y si y = u – v entonces dy / dx = du / dx – dv / dx.

Derivada del Producto (Teorema 3)

Enunciado : Si u y v son funciones diferenciables de x y si y = u v entonces

$\frac{dy}{dx} = u\;\frac{dv}{dx}\; + \; v \;\frac{du}{dx}$

Prueba:

Sean δu, δv y δy los pequeños incrementos en u, v, y respectivamente, correspondientes al incremento δx en x

Como δx ⇢ 0, δu⇢ 0, δv⇢ 0, δy ⇢ 0,

Como u y v son funciones diferenciables de x,

$\frac{du}{dx} = \lim\;_{\delta x \to0}\;\frac{\delta u}{\delta x} \; and \; \frac{dv}{dx}\lim\;_{\delta x \to0}\;\frac{\delta v}{\delta x}$

y = uv ⇢ eq. (1)

y + δy = (u + δu) (v + δv)

= uv + uδv + vδu + δuδv ⇢ eq(2)

Restando (1) de (2), obtenemos

δy = uδv + vδu + δuδv

Dividiendo ambos lados por δx,

δy / δx = u(δv / δx) + v(δu / δx) + (δu / δx)δv

Tomando límite como δx ⇢ 0, obtenemos

$\lim\;_{\delta x \to 0}\; \frac{\delta y}{\delta x} = u\lim\;_{\delta x \to 0}\; \frac{\delta v}{\delta x}\; + \; v\lim\;_{\delta x \to 0}\; \frac{\delta u}{\delta x}\; + \; \lim\;_{\delta x \to 0}\;\frac{\delta u}{\delta x}.\lim\;_{\delta x\to 0}\;\delta v$

= u (dv/dx) + v(du/dx) + (du/dx) × 0

Como RHS existe y es igual a (dy/dx),

$\frac{dy}{dx} = u\;\frac{dv}{dx}\; + \; v \;\frac{du}{dx}$

Así, la derivada del producto de dos funciones = primera función × derivada de la segunda función + segunda función × derivada de la primera función

Similarmente,

Derivada del cociente (Teorema 4)

Enunciado: Si u y v son funciones diferenciables de x y si y = u / v entonces

$\frac{dy}{dx} = \frac{v\frac{du}{dx} - u\frac{dv}{dx}}{v^2}$

Ejemplos de problemas

Pregunta 1: Encuentra la derivada de 3x + 4 usando el primer principio de la derivada.

Solución:

Sea f(x) = 3x + 4

f(x + h) = 3(x + h) + 4

considerar,

$\lim\;_{h \to 0} \; \frac{f(x + h) - f(x)}{h}$

$\lim\;_{h \to 0} \; \frac{3(x + h)\; + \; 4 \; - \;(3x + 4)}{h}$

$\lim\;_{h \to 0}\; \frac{3h}{h}$

= 3

∴ f'(x) = 3

Pregunta 2: Encuentra la derivada de

1 / x ² y
x porque x.

Usando el primer principio de la derivada.

Solución:

1 / ²

Sea f(x) = 1 / x ²

f(x + h) = 1 / (x + h) ²

Considerar,

$\lim\;_{h \to 0} \; \frac{f(x + h) - f(x)}{h}$

$\lim\;_{h \to 0} \; \frac{\frac{1}{(x+h)^2} - \frac{1}{x^2}}{h}$

$\lim\;_{h \to 0}\; \frac{x^2 - (x + h^2)}{h(x + h)^2 . x^2}$

$\lim\;_{h \to 0}\; \frac{x^2 - (x^2 + 2xh + h^2)}{h(x + h)^2 . x^2}$

$\lim\;_{h \to 0}\; \frac{-h(2x + h)}{h(x + h)^2 . x^2}$

$-\lim\;_{h \to 0}\; (2x + h)\;\;\lim\;_{h \to 0}\; \frac{1}{(x + h)^2 . x^2}$

= -2x( ¹^/ x2x2 )

= -2 / ^x3

∴ f'(x) = -2 / x ³

x porque x

Sea f(x) = x cos x

f(x + h) = (x + h) porque (x + h)

considerar,

$\lim\;_{h \to 0} \; \frac{f(x + h) - f(x)}{h}$

$\lim\;_{h \to 0} \; \frac{(x + h) cos (x + h) - x cos x}{h}$

$\lim\;_{h \to 0} \; \frac{x[cos (x + h) - cos x]+ h\;cos(x + h)}{h}$

$\lim\;_{h \to 0} \; \frac{x(-2)sin(x + \frac{h}{2})\;sin\frac{h}{2}}{2x\frac{h}{2}}\; + \; \lim\;_{h \to 0}\; \frac{h\;cos(x + h)}{h}$

$-x\;\lim\;_{h \to 0}\; sin (x +\frac{h}{2}).\; \lim\;_{h \to 0}\; \frac{sin\frac{h}{2}}{\frac{h}{2}}\;+\; cos(x + 0)$

= -x sen x. 1 + porque x

= -x sen x + cos x

∴ f'(x) = -x sen x + cos x

Pregunta 3: Diferencia lo siguiente

sen x / 1 + sen x
e ^x / 1 + sen x

Solución:

sen x / 1 + sen x

tenemos

y = sen x / 1 + sen x

$\frac{dy}{dx} = \frac{(1 + sin\;x) \frac{d}{dx}(sin\;x) - sin\;x \frac{d}{dx}(1 + sin\;x)}{(1+ sinx)^2}$

$=\frac{(1 + sin\;x).cos\;x - sin\;x. (0 + cos\;x)}{(1+ sinx)^2}$

$=\frac{cos\;x + sin\;x.cos\;x - sin\;x.cos\;x}{(1 + sin\;x)^2}$

= cos x / (1 + sen x) ²

e ^x / 1 + sen x

y = e ^x / 1 + sen x

$\frac{dy}{dx}\; = \frac{(1 + sin\;x)\frac{d}{dx}e^x\;-\;e^x\;\frac{d}{dx}(1 + sin\;x)}{(1 + sin\;x)^2}$

$=\frac{(1 + sin\;x).e^x\;-\;e^x.(0 + cos\;x)}{(1 + sin\;x)^2}$

$= \frac{e^x[1 + sin\;x - cos\;x]}{(1 + sin\;x)^2}$

Pregunta 4: y = log 5(log7 x) encuentra dy / dx

Solución:

tenemos,

y = registro ₅ (registro ₇ x)

Usando la propiedad logarítmica, podemos escribir,

y = logaritmo( logaritmo ₇ x ) / logaritmo 5

$\frac{dy}{dx} = \frac{1}{log\;5}.\frac{d}{dx}[log(log_7x)]$

$= \frac{1}{log\;5}\;.\;\frac{1}{\frac{log\;x}{log\;7}}\;.\;\frac{d}{dx}(\frac{log\;x}{log\;7})$

$= \frac{1}{log\;5}\;.\;\frac{1}{\frac{log\;x}{log\;7}}\;.\;\frac{1}{log\;7}\frac{d}{dx}(log\;x)$

$= \frac{1}{log\;5\;.\;.log\;x}\;.\;\frac{1}{x}$

= 1 / x registro 5. registro x

Pregunta 5: Si y = $log[\frac{x + \sqrt{x^2 + 25}}{\sqrt{x^2 + 25}-x}]$

Solución:

y = $log[\frac{x + \sqrt{x^2 + 25}}{\sqrt{x^2 + 25}-x}]$

y = $log\;(x + \sqrt{x^2 + 25})\; -\; log\;(\sqrt{x^2 + 25}-x)$

$\frac{dy}{dx} = \frac{1}{x + \sqrt{x^2+25}}\;.\;\frac{d}{dx}(x + \sqrt{x^2+25})\;-\;\frac{1}{\sqrt{x^2+25}-x}\;.\;\frac{d}{dx}(\sqrt{x^2 + 25}-x)$

$= \frac{1}{x+\sqrt{x^2+25}}\;(1 \;+\;\frac{1}{2\sqrt{x^2+25}}\times2x)\;-\;\frac{1}{\sqrt{x^2+25}-x}\;(\frac{1\times2x}{2\sqrt{x^2+25}}\;-\;1)$

$= \frac{1}{x + \sqrt{x^2+25}}\;[\frac{\sqrt{x^2+25}\;+\;x}{\sqrt{x^2+25}}]\;+\;\frac{1}{\sqrt{x^2+25}-x}\;[\frac{\sqrt{x^2+25}-x}{\sqrt{x^2+25}}]$

$= \frac{1}{\sqrt{x^2+25}}\;+\;\frac{1}{\sqrt{x^2+25}}$

$= \frac{2}{\sqrt{x^2+25}}$

Pregunta 6: Si y = log(3x ² + 2x +1), encuentra dy / dx

Solución:

y = logaritmo (3x ² + 2x +1)

$= \frac{dy}{dx} = \frac{1}{3x^2 + 2x + 1}\;\;\frac{d}{dx}(3x^2 + 2x + 1)$

$= \frac{1}{3x^2+2x+1}\;\;(6x +2)$

$= \frac{2(3x +1)}{3x^2 + 2x +1}$

Pregunta 7: Usando el primer principio de la derivada, encuentre √sen x

Solución:

Sea f(x) = √sen x

f(x + h) = √sen (x + h)

considerar,

$\lim\;_{h \to 0} \; \frac{f(x + h) - f(x)}{h}$

$= \lim\;_{h \to 0}\;\frac{\sqrt{sin(x + h)} \;-\;\sqrt{sin\;x} }{h}$

$= \lim\;_{h \to 0}\;\frac{\sqrt{sin(x + h)} \;-\;\sqrt{sin\;x} }{h} \; \times \;= \frac{\sqrt{sin(x + h)} \;+\;\sqrt{sin\;x} }{\sqrt{sin(x + h)} \;+\;\sqrt{sin\;x}}$

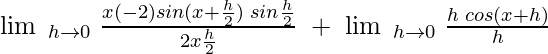
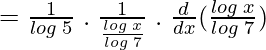
$= \;\lim\;_{h \to 0}\; \frac{sin(x + h) - sin\;x}{h[\sqrt{sin(x + h)} \;+\; \sqrt{sin\;x} ]}$

$= \lim\;_{h \to 0}\; \frac{2 cos\;(\frac{x + h+ x}{2})\;.\;sin\;(\frac{x + h - x}{2})}{h[\sqrt{sin(x + h)}\; +\;\sqrt{sin\;x} ]}$

$= \lim\;_{h \to 0}\; \frac{2\;cos\;(x +\frac{h}{2})\;.\;sin(\frac{h}{2})}{h[\sqrt{sin(x + h)\;+\;\sqrt{sin\;x}}]}$

$= \lim\;_{h \to 0}\; \frac{\;cos\;(x +\frac{h}{2})}{\sqrt{sin(x + h)\;+\;\sqrt{sin\;x}}}\;\times\;\frac{sin(\frac{h}{2})}{(h/2)}$

$=\frac{\lim\;_{h \to 0}\;cos\;(x +\frac{h}{2})}{\lim\;_{h\to 0}\;\sqrt{sin(x + h)\;\;+\sqrt{sin\;x}}}\;\times\;\lim\;_{h \to 0}\;\frac{sin(\frac{h}{2})}{(h / 2)}$

$=\frac{cos\;x}{\sqrt{sin\;x}\;+\;\sqrt{sin\;x}}\;\times1$

$.....[h \to 0, \frac{h}{2} \to 0 \;and\;\lim\;_{\theta \to 0}\;\frac{sin\;\theta}{\theta} =1]$

$= \frac{cos\;x}{2\sqrt{sin\;x}}$