¿Cómo encontrar asíntotas verticales y horizontales?

Una función es un tipo de operador que toma una variable de entrada y proporciona un resultado. Cuando una cantidad depende de otra, se crea una función. Una propiedad interesante de las funciones es que cada entrada corresponde a una única salida. En otras palabras, tal operador entre dos conjuntos, digamos el conjunto A y el conjunto B, se llama función si y solo si asigna cada elemento del conjunto B a exactamente un elemento del conjunto A. Cuando todos los valores de entrada y salida se trazan en el plano cartesiano, se denomina como el gráfico de una función.

Asíntotas

Tales líneas imaginarias que están muy cerca de la gráfica completa de una función o un segmento de la gráfica se llaman asíntotas. Al graficar una función, las asíntotas son muy útiles ya que te ayudan a pensar qué líneas no debe cruzar la curva. Una asíntota, en otras palabras, es un punto en el que converge la gráfica de una función. Cuando graficamos funciones, rara vez necesitamos dibujar asíntotas.

Tipos de asíntotas

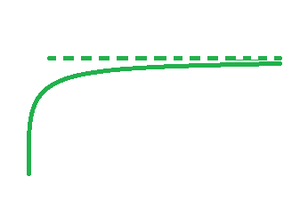
• Asíntotas horizontales: una asíntota horizontal es una línea horizontal que muestra cómo se comporta una función en los bordes extremos del gráfico. Sin embargo, es muy posible que la función pueda cruzar la asíntota e incluso tocarla. Para funciones con polinomio numerador y denominador, existen asíntotas horizontales. Las expresiones racionales son el nombre de estas funciones. Una forma horizontal de una función se da como y = k.

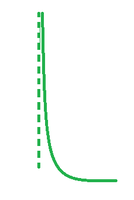
• Asíntotas Verticales: Una asíntota vertical es una recta vertical que dirige pero no forma parte de la gráfica de una función. La gráfica nunca la cruzará ya que sucede en un valor de x que está fuera del dominio de la función. Puede haber más de una asíntota vertical para una función.

Encontrar asíntotas horizontales

Para calcular las asíntotas horizontales, el punto de consideración son los grados tanto del numerador como del denominador de la función dada. Los criterios para determinar las asíntotas horizontales de una función son los siguientes:

• Cuando el numerador y el denominador tienen el mismo grado: Divide los coeficientes de las principales variables para encontrar la asíntota horizontal.
• Si el grado del numerador es menor que el del denominador: La asíntota horizontal se encuentra en y = 0, es decir, el eje x.
• Si el grado del numerador es mayor que el del denominador: No hay asíntota horizontal para la función racional dada.

Encontrar asíntotas verticales

Hay dos pasos a seguir para determinar la asíntota vertical de las funciones racionales. Estos son:

Paso I: Reduzca la función racional dada tanto como sea posible eliminando los factores comunes y simplificando el numerador y el denominador a través de la factorización.

Paso II: iguale el denominador a cero y resuelva para x. Los valores de x son las asíntotas verticales de la función.

Problemas de muestra

Problema 1. Encuentra las asíntotas horizontal y vertical de la función: f(x) =  .

Solución:

Asíntota horizontal:

Grado del numerador = 2

Grado del denominador = 1

Como el grado del numerador es mayor que el del denominador, la función dada no tiene asíntota horizontal.

Asíntota vertical:

Dado que la función ya está en su forma más simple, iguale el denominador a cero para determinar la(s) asíntota(s) vertical(es).

⇒ x + 5 = 0

⇒ x = −5

Problema 2. ¿Puede una función cuadrática tener asíntotas?

Solución:

Una función cuadrática es un polinomio, por lo que no puede tener ningún tipo de asíntotas. Dado que las funciones polinómicas están definidas para todos los valores reales de x, no es posible que una función cuadrática tenga asíntotas verticales. Además, dado que la función tiende a infinito como lo hace x, tampoco existe asíntota horizontal. 

Problema 3. Halla las asíntotas horizontal y vertical de la función: f(x) =  .

Solución:

Asíntota horizontal:

Grado del numerador = 2

Grado del denominador = 2

Como el grado del numerador es igual al del denominador, la asíntota horizontal se determina dividiendo los coeficientes principales.

⇒ HA = 2/2 = 1

Asíntota vertical:

La función necesita ser simplificada primero. 

Ahora que la función está en su forma más simple, iguala el denominador a cero para determinar la asíntota vertical.

⇒ x + 1 = 0

⇒ x = −1

Problema 4. Encuentra las asíntotas horizontal y vertical de la función: f(x) = 10x ² + 6x + 8.

Solución:

La función dada es cuadrática. Una función cuadrática es un polinomio, por lo que no puede tener ningún tipo de asíntotas. Dado que las funciones polinómicas están definidas para todos los valores reales de x, no es posible que una función cuadrática tenga asíntotas verticales. Además, dado que la función tiende a infinito como lo hace x, tampoco existe asíntota horizontal. 

Problema 5. Halla la asíntota horizontal de la función: f(x) = 9x/x ² +2.

Solución:

Grado del numerador = 1

Grado del denominador = 2

Como el grado del numerador es menor que el del denominador, la asíntota horizontal viene dada por: y = 0.

Problema 6. Halla las asíntotas horizontal y vertical de la función: f(x) = x+1/3x-2.

Solución:

Asíntota horizontal:

Grado del numerador = 1

Grado del denominador = 1

Como el grado del numerador es igual al del denominador, la asíntota horizontal se determina dividiendo los coeficientes principales.

⇒ HA = 1/3

Asíntota vertical:

La función está en su forma más simple, igualar el denominador a cero para poder determinar la asíntota vertical.

⇒ 3x – 2 = 0

⇒ x = 2/3

Problema 7. Halla las asíntotas horizontal y vertical de la función: f(x) = x ² +1/3x+2.

Solución:

Asíntota horizontal:

Grado del numerador = 2

Grado del denominador = 1

Como el grado del numerador es mayor que el del denominador, la función dada no tiene asíntota horizontal.

Asíntota vertical:

Dado que la función ya está en su forma más simple, iguale el denominador a cero para determinar la(s) asíntota(s) vertical(es).

⇒ 3x + 2 = 0

⇒ x = −2/3